calculation of bolted joint forces

[s_c_90]

Hello everyone, I am new to the forum so I apologize in advance if I commit some label error.
I have been working on the fem model of a single lap audition in composite bullonate; one of the two plates is stuck at the end, while the end of the other plate is loaded with a traction force.
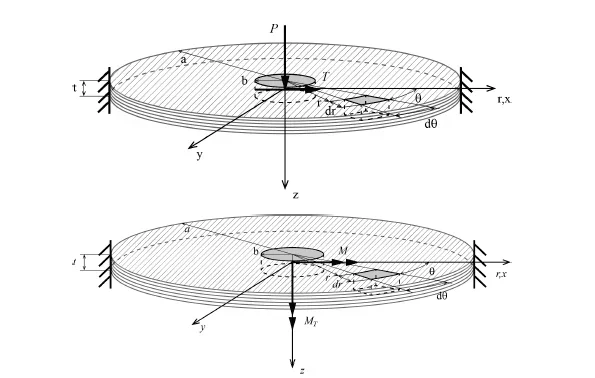
the purpose of the study is to validate whether it is possible or not to compare the behavior of the plates that compose the test to that of a circular plate with external radius framed and with a rigid lock at the center that simulates the behavior of the bolt and on which the loads are concentrated. therefore I need to extrapolate the loads agents on the plates from the fem model of the test.
I have done several tests considering the fsum or nforce command and selecting the nodes and elements within one of the two plates or considering a half of the bolt; Unfortunately, the results are not satisfactory.
the question that I ask you is therefore whether according to you is correct the procedure followed to calculate the loads agents or if it is totally free of principle.
Thank you all in advance

 

[Stan9411]

without images you don't understand anything ... compare a test to a plate with a rigid block that simulates a bolt...
Can you try to explain the problem more clearly?

 

[s_c_90]

The proof I'm considering is the one in the attached image. at the left end there is a recess while on the right there are loads and trolleys that block the long z translations to avoid rigid motions.
the purpose is to demonstrate that it is possible to characterize the behavior of the audition with an equivalent model in which all the quantities (posts, deformations and tensions) are calculated analytically. the equivalent model consists of a circular plate with framed contour and with a central rigid block, so you have the boundary conditions to solve the equations. the unknown of the analytical problem is the outer radius of the circular plate of the equivalent model that allows to approximate to the best the deformed of the upper (or lower) plate of the test.
in the equivalent model, the plate can be loaded only with forces acting on the rigid central lock and therefore I need to know what are the agents loads on the central core, which in the fem model is represented by the bolt.
I hope I've been clearer

 

[Stan9411]

mmmm from the description you make it looks like you want the screw to work. a bolted joint always works and anyway for friction, so unless pushes that you have however canceled by adding a cart, the only effort that will feel will be that of traction, necessary to generate the load that does not slide the platelets between them, and torsion. Knowing the force applied to the plate and friction coefficient, calculating the forces agents on your “central core” seems trivial. . Maybe I'm losing something, but if you expect loads so much to request a fem analysis, it means you're not working your joint like a bolt properly said

 

[s_c_90]

fem analysis is necessary to go to calculate rotation and all other sizes related to one of the two plates so that you can compare. doing the "hand" calculations of the agent force on the bolt results are very distant from those I should get.
By reading articles related to problems similar to mine, the loads agents on the plates, besides clearly to the traction load, should be a long tilting moment y and a transversal force on the plate plane. so I was using the fsum command to try to figure out what was the entity of this moment that is present due to the non symmetry of the junction.
can it be correct as a way of proceeding?