Axe du faisceau neutre de trajectoire avec section variable non symétrique

[Vaik]

Bonjour.
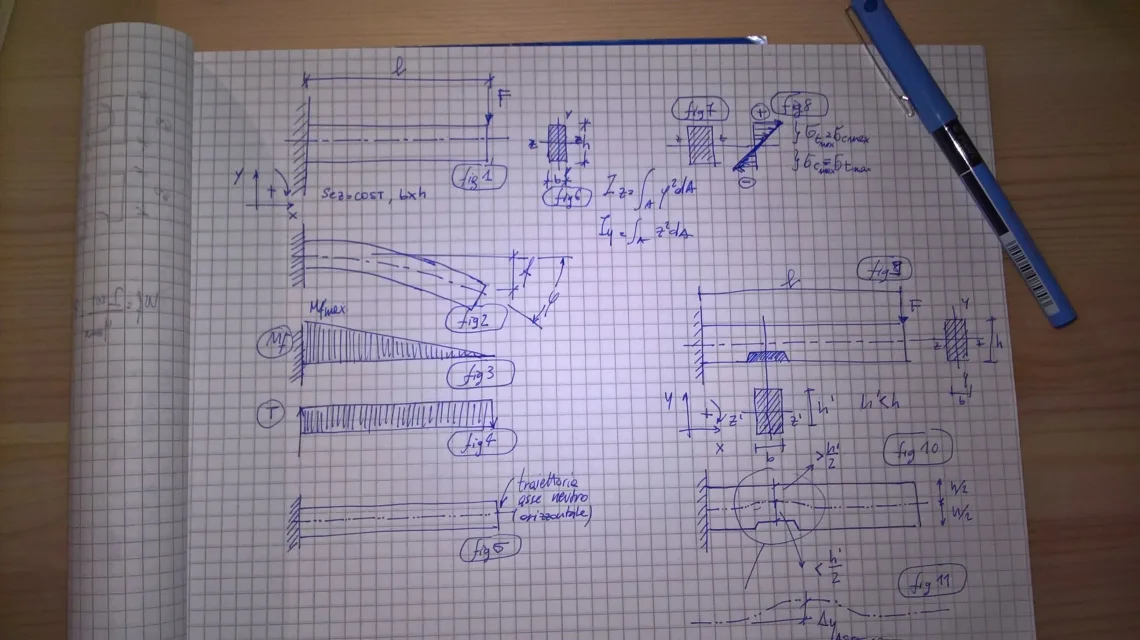
après avoir cherché longtemps sur le web et sur le forum lui-même concernant ce qui est rapporté dans le titre, sans trouver de réponse exhaustive, j'écris ces lignes. Je me référerai au schéma que j'ai joint. aussi spécifique que quand j'écris "un", je veux dire "axe neutre".
Ma question est la suivante :
comment puis-je déterminer la position de l'axe neutre avec lequel calculer le module d'inertie de surface du second ordre (i [mm^4] ) dans un faisceau avec des sculptures, des variations de section ?

Mon raisonnement est le suivant :
exemple a:
Je commence à partir de l'exemple simple d'un faisceau de section constante (par exemple rectangulaire bxh), fig1, collé à un extrême et chargé de force concentrée à l'extrême opposé. l'axe neutre auquel le moment d'inertie izz, dans cette configuration, coïncidera avec l'axe de symétrie z-z, fig6. Pas de problème.

exemple b:
Si j'ajoute maintenant une fente comme dans la fig9, enlevant du matériel, je reçois, en correspondance de la coupe que j'ai opéré, une section bxh', avec h'<h. Je dois penser à la position de l'axe neutre dans cette section, je serais spontané pour le placer aussi en demi-essai et donc coïncider avec z'-z' (fig9 ).

considérant maintenant tout le faisceau de fig9 le long de sa plus grande taille et affichant ainsi la trajectoire des positions successives de l'axe neutre pour chaque section qui le compose, je obtiendrais une ligne cassée avec un motif similaire au bord inférieur du même faisceau de fig9 qui passe exactement pour les demi-points de chaque section laissant tant de matériau de traction au-dessus, comme matériau en compression ci-dessous (je n'ai pas préparé d'image dans le diagramme... ).

d1) Est-ce un résultat correct et sincère?
d2) ou la trajectoire ci-dessus est plutôt celle de la fig.10 et de la fig11 ? ou la trajectoire de l'axe neutre subit une variation de γy, par rapport à la position obtenue en calculant selon l'exemple a, qui place l'axe neutre de la section bxh (à proximité de l'écart) à une "demi-voie" entre la position de l'axe neutre de l'exemple a et l'exemple b.

d3) si la question est affirmée d2, alors comment peut-on la quantifier? Pourriez-vous approcher la position moyenne entre ceux obtenus par exemple a et l'exemple b?

J'ai essayé de me donner une réponse en reproduisant des exemples avec le fem inventeur, et j'ai aussi cherché des plug-ins autocad qui ont calculé la position de l'axe neutre, mais rien de satisfaisant.
S'il y a des ingénieurs qui ne peuvent également se référer qu'à un lien (également en anglais) qui explique exactement ce qu'ils ont demandé, je vous serais reconnaissant!
dans le calcul de la position de l'un j'ai pensé à l'équilibre que les sections qui sont au-dessus et au-dessous de l'axe neutre doivent respecter, mais ne retournent toujours rien.

 

[meccanicamg]

Malheureusement, toute la théorie faite sur les livres tient compte du fait que la section reste constante le long du faisceau. Par conséquent, en termes de variations de section, une section moyenne du profil doit être considérée, valide du début à la fin. L'accidentalité, c'est-à-dire les variations de section, doit être évaluée localement avec des coefficients de coupe et ce qui est autre chose et non comme modèle de calcul réel.
ce qui peut être très proche de la réalité sera un fem précis. Ce n'est qu'ainsi que vous pourrez valider localement la théorie des médias retouchés.
Malheureusement, il n'y a pas d'autres voies qui puissent être tracées à la réalité.
donc l'axe neutre est le faisceau moyen comme s'il n'avait pas de sculptures.

 

[Vaik]

Malheureusement, toute la théorie faite sur les livres tient compte du fait que la section reste constante le long du faisceau. Par conséquent, en termes de variations de section, une section moyenne du profil doit être considérée, valide du début à la fin. L'accidentalité, c'est-à-dire les variations de section, doit être évaluée localement avec des coefficients de coupe et ce qui est autre chose et non comme modèle de calcul réel.
ce qui peut être très proche de la réalité sera un fem précis. Ce n'est qu'ainsi que vous pourrez valider localement la théorie des médias retouchés.
Malheureusement, il n'y a pas d'autres voies qui puissent être tracées à la réalité.
donc l'axe neutre est le faisceau moyen comme s'il n'avait pas de sculptures.

suggérer que vous considérez la plus grande section de noisette tout résistant. Un peu comme vous quand vous taillez un arbre qui a un onglet. en cas de calibrage, compte tenu des coefficients de sécurité et de surdimensionnement est correct et légal.
Cependant, si vous voulez comparer deux sections, toutes deux avec des formes qui ne partagent pas les mêmes axes principaux d'inertie, dont je peux encore calculer le moment d'inertie et identifier la position des axes principaux d'inertie (mon cas pour lequel j'ai résolu l'intégrale puis vérifié avec autocad la véracité des résultats). Je dois renvoyer les deux sections à un axe choisi arbitrairement, mais néanmoins parallèle au principal, puis recalculer le moment d'inertie des sections pris en compte en le comparant? Peut-il être correct ou n'a pas de sens ?

 

[meccanicamg]

dans le cas où vous avez deux poutres avec une section différente, vous devez considérer la géométrie moyenne des deux sections et les évaluer pour les deux axes principaux de l'inertie.
la méthode est comme l'arbre avec un onglet.

 

[Vaik]

Merci pour l'intervention rapide à laquelle vous avez répondu!
Je vais faire d'autres calculs comme exemple parce que c'est très curieux pour moi.
J'afficherai ces exemples au cas où pour conclure la discussion et en tirer des conclusions et pour vérifier que j'ai bien compris ce que vous voulez dire.

Si quelqu'un d'autre veut ajouter quelque chose, allez-y. même toute suggestion sur un logiciel ou des méthodes pour localiser un serait bien acceptée.

 

[meccanicamg]

Merci pour l'intervention rapide à laquelle vous avez répondu!
Je vais faire d'autres calculs comme exemple parce que c'est très curieux pour moi.
J'afficherai ces exemples au cas où pour conclure la discussion et en tirer des conclusions et pour vérifier que j'ai bien compris ce que vous voulez dire.

Si quelqu'un d'autre veut ajouter quelque chose, allez-y. même toute suggestion sur un logiciel ou des méthodes pour localiser un serait bien acceptée.

Alors comment s'est terminé le calcul de l'hypothèse simpliste ?