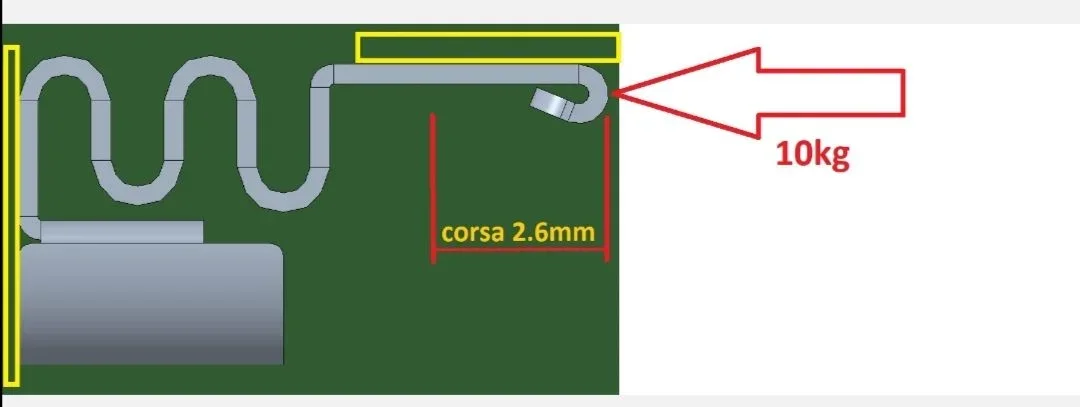
J'ai essayé de faire quelques fems pour comprendre comment ça se passe.
D'abord j'ai encadré l'onglet en arrière et j'ai maintenu l'onglet aligné sur un plan avec seulement la réaction normale comme indiqué par vous et chargé avec une force f l'avant.
Les simulations sont linéaires. comme d'abord je me retrouve en appliquant 10kg, c'est-à-dire
100n au modèle j'ai une compression
0,2 mm et non la valeur 2.6 que vous avez indiquée.
Voir la pièce jointe 54971donc je pense que nous avons tort de la charge à appliquer, alors il sera 100kg =
1 000n et voir ce qui se passe.
Voir la pièce jointe 54972Maintenant nous nous trouvons un mouvement
2,35 mm....quand nous sommes là mais les tensions de von mises? nous avons des pics
22100pa dans la plage inférieure de l'onglet horizontal (impossibilité de résister à ces valeurs).
Voir la pièce jointe 54973À ce stade, il y a des considérations à faire:
- pour mieux comprendre, il faudrait affiner le maillage à ce point et voir si les valeurs sont stables ou non
- prendre les caractéristiques mécaniques de l'acier et réaliser un fem non linéaire
- peut-être que les charges sont excessives, peut-être que vous ne devriez pas faire
2,6 mm Peut-être que quelque chose dans les données est mal
nous recherchons les caractéristiques mécaniques d'un acier au silicium pour ressorts
52 (rm=2500mpa rp0.2=1780mpa et a=5%) et nous obtenons tous les paramètres à insérer dans le simulateur en utilisant la vraie courbe, puis réaliser un fem complètement non linéaire.
Voir la pièce jointe 54975sur le premier tour le fem fournit comme erreur le fait qu'il y a des différences dans les itérations. donc nous passons de la méthode de calcul des matrices de
standard a....tous... y compris ça
itératifIl n'y a rien à faire alors on s'adapte au maillage et on voit ce qui se passe... rien à faire. il est nécessaire de baisser la charge et essayer de la régler à
200n.
Voir la pièce jointe 54976ici nous pouvons voir les domaines soumis à la plastification, c'est-à-dire qu'ils ont des tensions de von mises plus grandes que le rendement (rp0.2) et qu'ils sont dans le domaine des déformations élasto-plastiques.
par définition tout ce qui est plastifié maintient une certaine déformation permanente qui ne reviendra jamais à l'origine. dans ce cas, vous avez une compression d'environ
0,94 mm.
les résultats que nous obtenons sont plus corrects qu'une analyse linéaire parce qu'à l'élongation égale d'epsilon correspondent aux tensions les plus basses et cela signifie que nous utilisons le champ plastique du matériau.
Il y a certainement des données de projet qui doivent être vérifiées fiscalement.