The techniques available as drivers of adapters in process composer are great. They are a result of in-depth research in numerical methods. The most prominent techniques are DOE, Optimization, Approximations, Six-Sigma. We have discussed DOE in detail in previous blogs. In this blog we are taking a deep dive into Optimization. Let’s not forget that we are in process composer, so the optimization is parametric primarily driven by geometric or physical parameters.
The Classical Optimization Definition
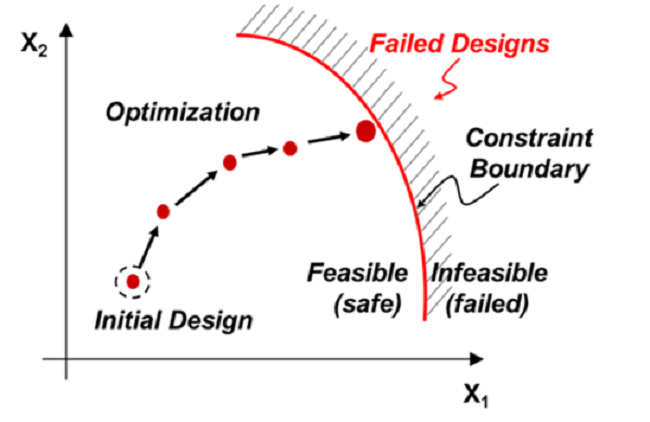
You have a ball somewhere in the fenced field. You have a starting point. You need to find the ball by traveling the minimum distance without crossing the fence. You have sensors for assistance. The ball is the Objective function. The fences are constraints. The sensors are the optimization techniques used.

The Difference between Design of Experiments and Optimization
The difference between the two is the same as difference between “better” and the “best”. Design of Experiments is a method to pick the most appropriate design point in an efficient manner from a pool of existing set of points. This set can either be defined by the user or by the DOE itself. The optimization techniques begin with a single initial design point and iteratively navigates in design space to get to the optimal or the best design point. Depending on the problem, the DOE can be a precursor to Optimization.
Types of Optimization Techniques
There are different methods to categorize them depending on how the objective function is defined and the type of suitable design space.
Constrained Techniques: They use separate functions to operate, one for the objective and the other for the constraints. We all have seen such techniques at some level during engineering courses. They are the most common ones.
Minimize/Maximize F(x) in x1>x>x2
Subject to: h(x)>a1; g(x)>a2; f(x)=0 etc.
Unconstrained Techniques: They use just one function for both objective and constraints. The user still defined constraints separate from the Objective but internally the constrained problem is converted to an unconstrained problem.
Based on the application to different types of design space, optimization methods can be classified Gradient based, Direct or Exploratory. The abbreviations shown in images below are the names of methods in respective categories.
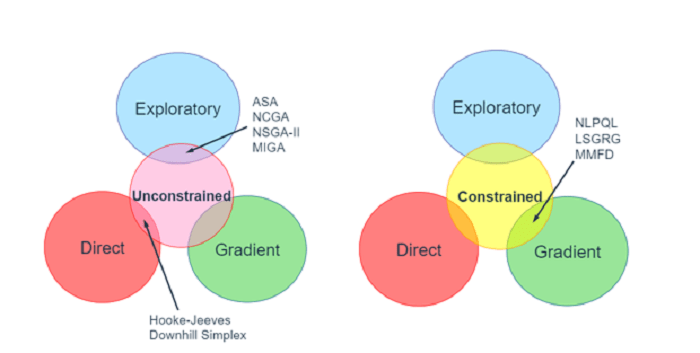
Gradient Methods: They are the oldest ones and have been well tested in the industry. They work on the principle of minimum energy or maximum stability. You gently drop a ball in a valley, and it will slide along the path of steepest decline until it reaches the lowest point in its vicinity. These methods work in continuous design space which has C0 and C1 continuity. They are likely to get stuck in the local minima so the initial point should be carefully picked.

Direct Methods: A direct search algorithm starts with a base point. It searches a set of points around it looking for one where the value of objective function is lower than the current one. The algorithm jumps to that point as a new base point and searches for a new set of points around it. One can figure out that such a method is computationally efficient as no gradient calculation is required. It’s more versatile as C0 and C1 continuity are not required. The most common ones are Hooke’s-Jeeves and Downhill Simplex.
The Hooke’s Jeeves method keeps track of its direction of travel. It does not change its direction with every step if a lower point is available in the direction of travel.

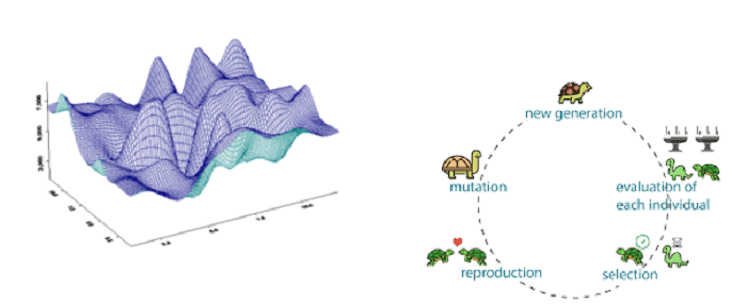
Exploratory Methods: These methods are based on cross over or mutation techniques among one data set of points called as parents to generate another data set of points called as children. The new data set evolves with each mutation, and it gets closer to the optimal solution. This is a high fidelity scheme that works with all kinds of objective functions: discontinuous, non-differentiable, stochastic, mixed integer type and highly non linear with multiple peaks and valleys as shown below. However, it is the most expensive optimization scheme in terms of computational expense. The most common methods are genetic algorithm, particle swarm and adaptive simulated annealing.
Pointer based methods: This is a mix and match approach in case the user has no clue which type of technique would be most suitable to solve the problem with reasonable accuracy. The pointer approach might help when user encounters an unfamiliar type of design space which is hard to visualize. Pointer method can utilize up-to three optimization schemes, preferably one from each basket: gradient, direct, and exploratory. As the optimization proceeds, the algorithm tracks the efficacy of each method and uses the one most appropriate for the given problem.

