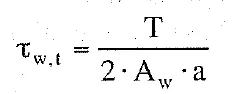I think they're the usual tricks of teachers who don't know how to saw students... and as always I don't understand why you have to work with rays and not with the diameters....however we come to us.
the key information is:
- straight teeth gear
- primitive diameter 312 mm
- tooth number 52
- wheel number 20
- width b=90 mm
Now you can get the most important thing, that is the module.
since d = m*z is obtained
m=d/z=312/52=6 mmand so we could calculate all the characteristics of the two gears.
Now we see that a weldable steel could be a construction steel or a remediation steel (with special measures). as we imagine that we are "poor" and we have to realize a large number of gears without fatigue, we will use an automatic construction steel like 11smnpb37 which is the same as
9smnpb36 uni4838 untreated, characteristics according to iso6336-5 image 5/6 (ml).
this steel
9smnpb36 has the following mechanical characteristics:
σflim tooth foot fatigue limit = 140 mpa
hertz σhlim pressure fatigue limit = 360 mpa
σb break resistance = 380 mpa
yield limit σs = 370 mpa
using the formula of lewiss and then evaluating the ability of the tooth foot to resist bending (objective for lewiss
σb / σf = 1), with only static case you have a 90 mm wide gear module 6 with the mechanical characteristics listed above and carries about one
pair of 9300nm. and this is the first value to set aside as a transferable couple.
Remember that if you don't have a rotating regimen, you can't do hertz contact pressure life reduction and so you don't have any other parameters you can use.
Now let's see the tab seat....and I see that you don't take into account the size/verification to specific pressure but only to specific pressure and this is wrong because you get a small tab that is actually unable to bear the load you calculated.
Moreover you do not only have to verify the tab that is in c45k but also the seat on the shaft and the hub that is in material with lower mechanical characteristics, so to greater reason you can not hold 500mpa of specific pressure permissible because the wheel will print if you use the pair so calculated. in the case with 9300nm I would need at least a 129 mm long tongue admitted that tree and central part of the hub is in c45 or in c50.
being that the hub is only 100 mm wide I have to maximize the thing and then I will get
n°2 languages arranged at 120° between them.
remember that for normal mechanics the admissible values are given using a 1.5 coefficient on yielding (if ductile materials) and 3 on breakage (if fragile materials).
then transmissible couple with a tab we say about
5000nm and with two tabs as from maximum capacity tooth.
now we go to see the welding, according to norms in force and not old and obsolete methods of calculation no longer valid (see ex cnr uni 10011 that has died and buried for decades) but we use eurocode 3
uni en iso 1993-1-8 and 1993-1-9 (if we want to do fatigue analysis of the joint welded).
instead of adopting the directional method, we adopt the simplified method of the standard (valid for angle and head joints), which provides a unit load capacity of the cord.
the formulas in play are as follows:
we calculate how much it is able to bring our welding cord:
fw,rd = 380 mpa * (6*1.41) / (0.9*1.25*1.73) = 1651 n/mmNow let's go figure out how much it works on the cords. as the performance of the force multiplied by arm turns out triangular for the couple to be constant we will have that the central cord + the outer cord will bring (it occurs) all the pair.
(c)
f1*96/2 + f2*276/2 = 9300*1000 nmm from which if I place the torque equal to zero
f1/f2 = d/d= 2.875So by doing the equation and trying to get the two forces to design that pull the two strings (of which each one is double in length) I will have:
fw,ed1 = f1=97000n/(6.28*96) = 160 n/mm
fw,ed1 = f2=34000n/628*276) = 20 n/mm
Is it true that both fw, and are less than fw,rd? Yes, then at the end of the fair, if I put two tabs and make the welds with triangular strings z=6 I will get that I will be able to transmit all the couple that can carry the tooth, being the weakest element.
Welding cords that hold ribs of ribs carry compression when the radial force of the gear is located above them and therefore finds itself reacting for the toothed crown with implode. if the ribs are of adequate measure the welding, at practical level, is almost useless in the sense that it brings a little compression but very little compared to the efforts in play in other areas. But you can calculate.
Also check:
keep in mind k1=k2=1 if the joint is in Class i and therefore must be a maximum quality joint and therefore belongs to the b category of the old uni 7278. alternatively, as written above, will be a joint in class ii less restrictive and grosser.
while polar moments for bending are the following:
Here below I attach an exercise of fatigue dimensioning with a somewhat different process and it is taken from the German norms (dv 925) of the metal/bridge/ferrovia construction sectors etc., but as you can see the formulas adopted for this verification are these of the j...w....
and you can simplify with the formula of bredt:
