meccanicamg
Guest
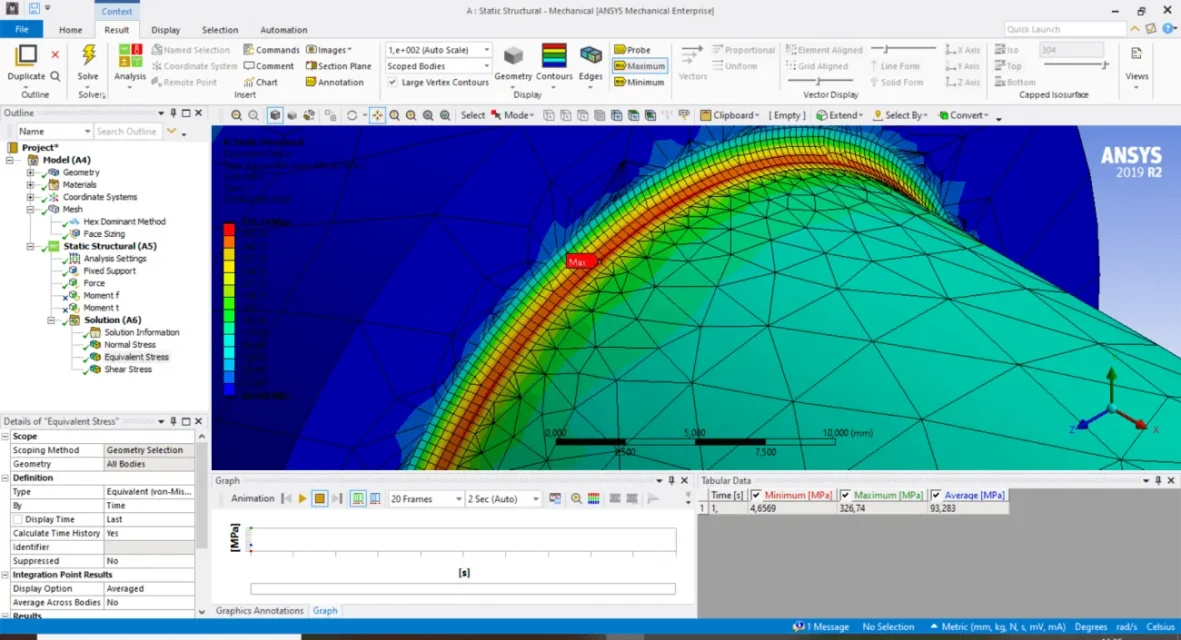
I tried to make a fem using freecad for the tree at two steps 45/30mm with radius 1 mm and 300nm of torque mopment.
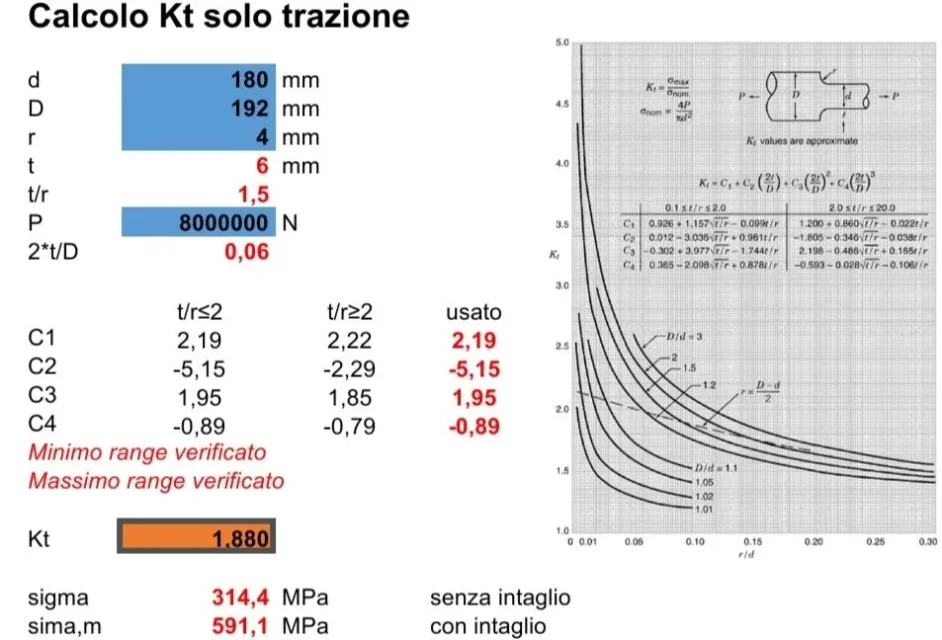
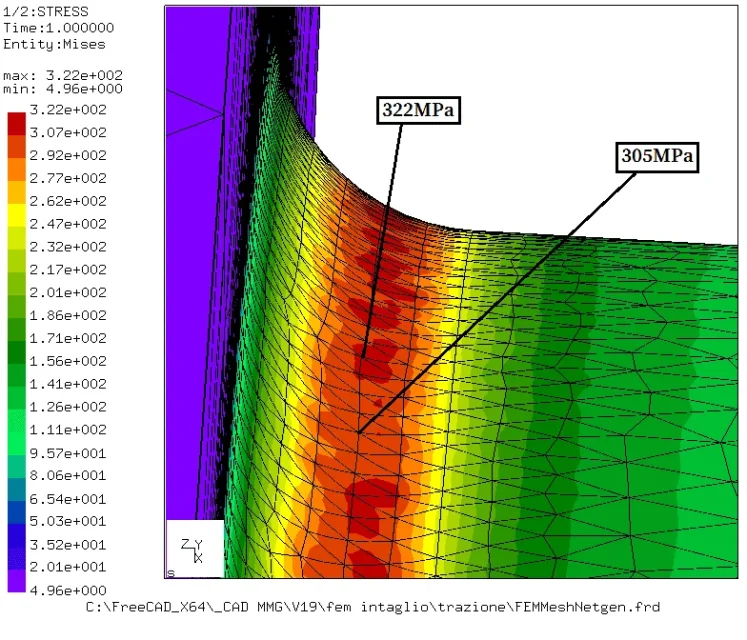
I don't really get your result. you have 300mpa but I would say it's wrong.
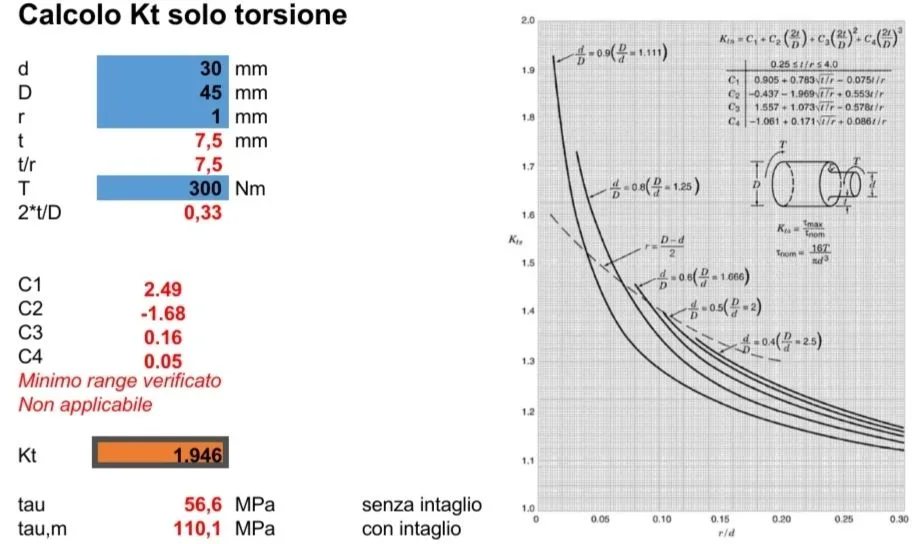
If you only have a torque moment, you only have 35.6mpa of tension that is what is also calculated by hand with the theoretical formula.
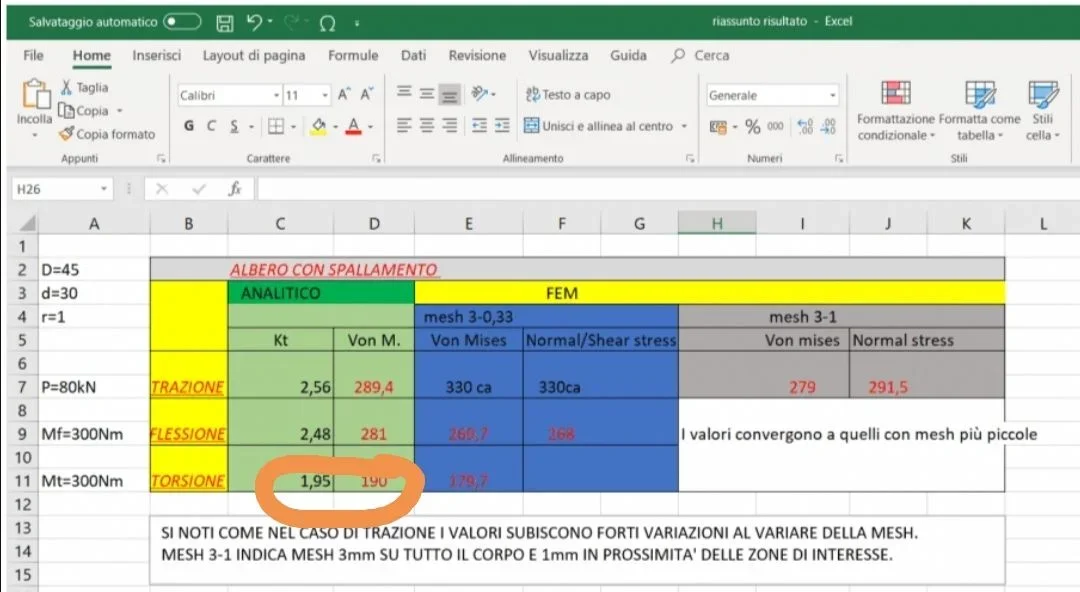
I took the tree where every diameter is 3 times long, so that it has a homogeneous behavior.
analyzing von mises, which is the most traditional approach that can be done, one has that the theoretical value tension is correct and one can read it quietly on the stretch 3 times the diameter.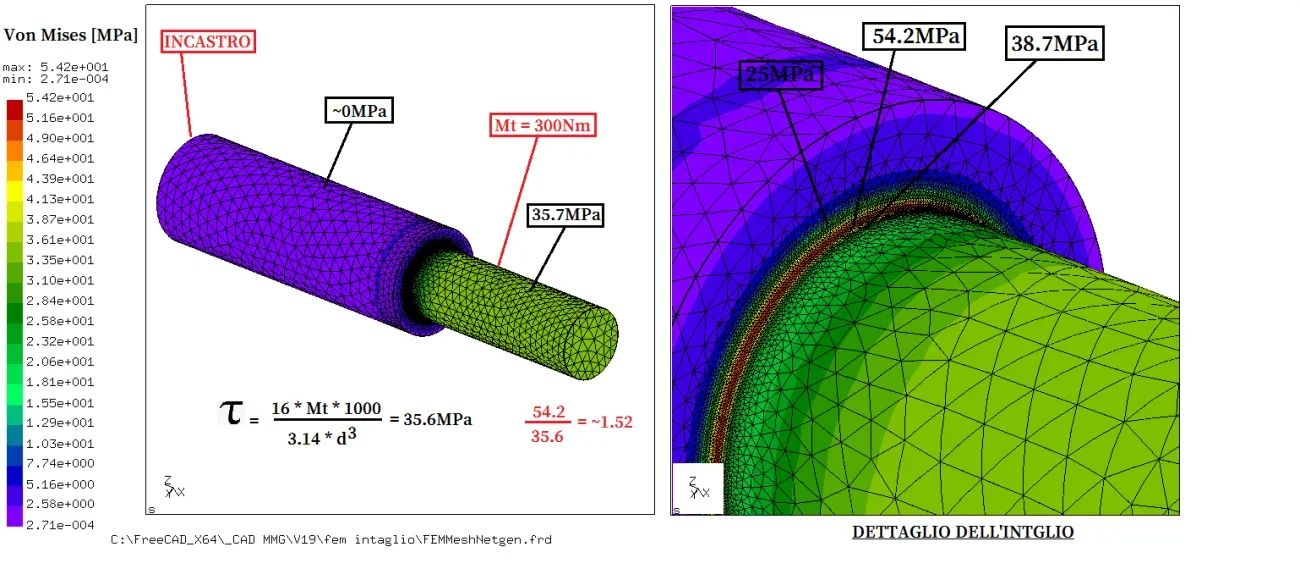 in the zone of the radius of 1 mm I made a mesh that divides in 4 the radius and the maximum value turns out to be 54.2mpa that is the tension that we expect on the connection radius.
in the zone of the radius of 1 mm I made a mesh that divides in 4 the radius and the maximum value turns out to be 54.2mpa that is the tension that we expect on the connection radius.
the same assessment was made by evaluating the main stress: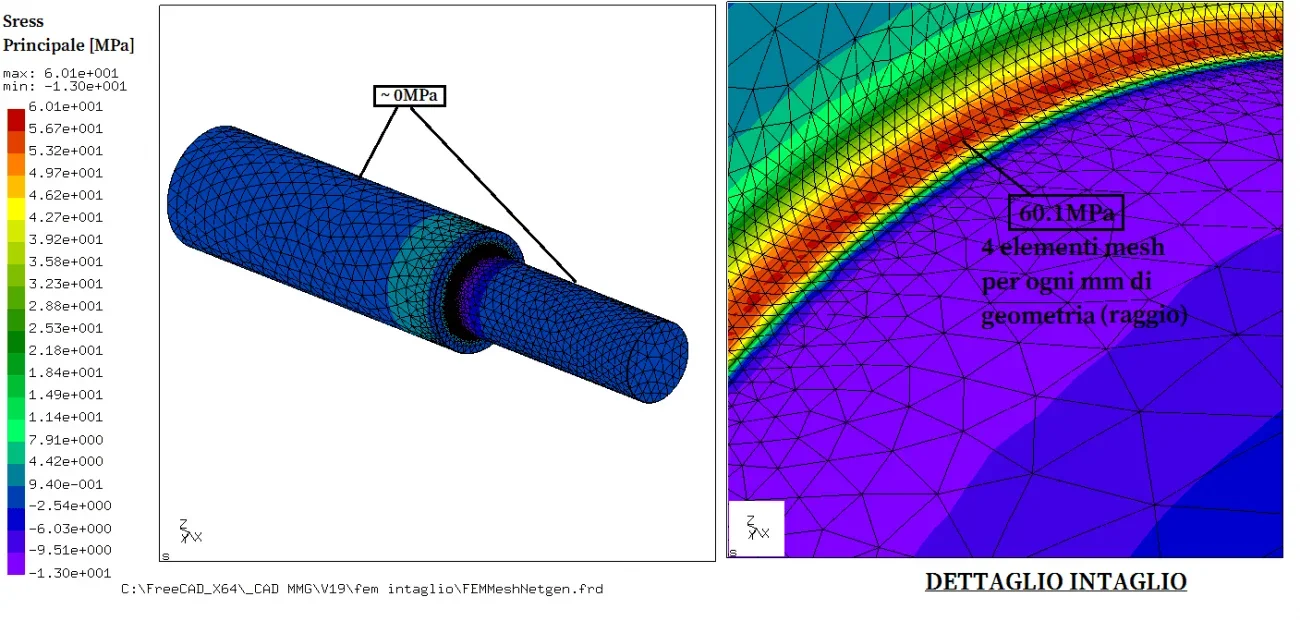 also here we have an intensification of the main tension that from zero passes to 60.1mpa which is the localized traction.
also here we have an intensification of the main tension that from zero passes to 60.1mpa which is the localized traction.
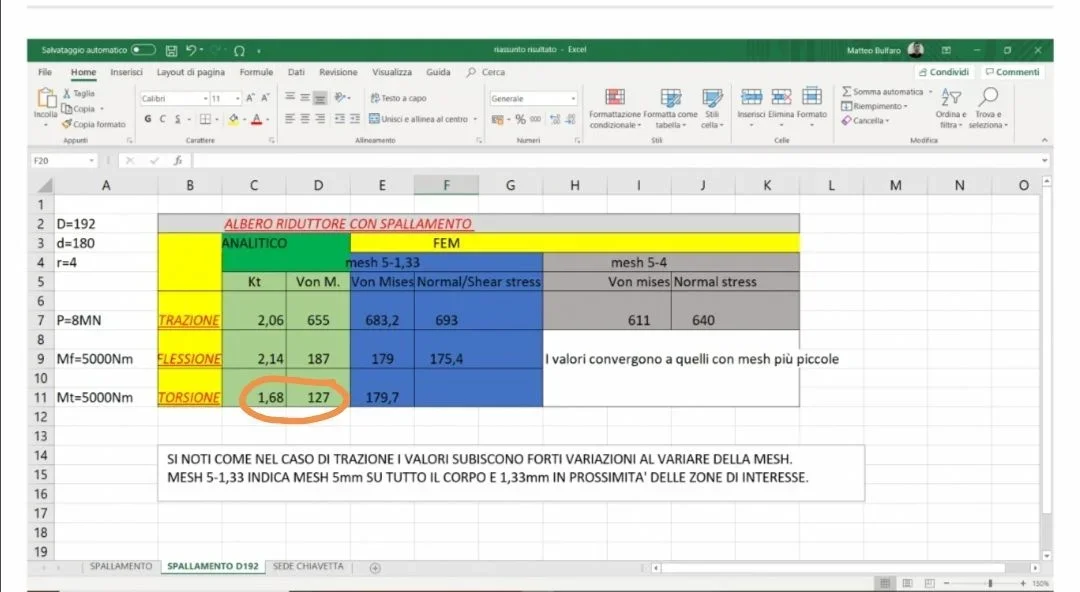
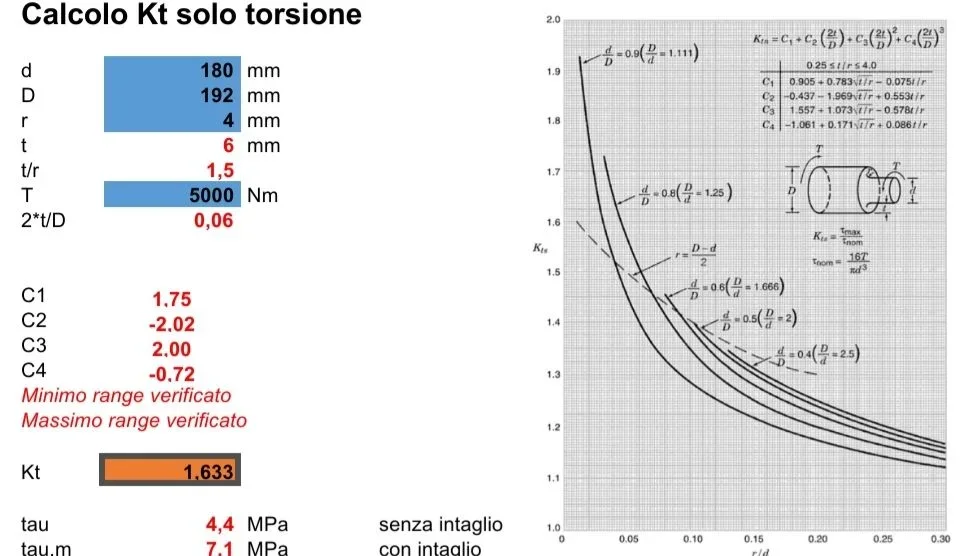
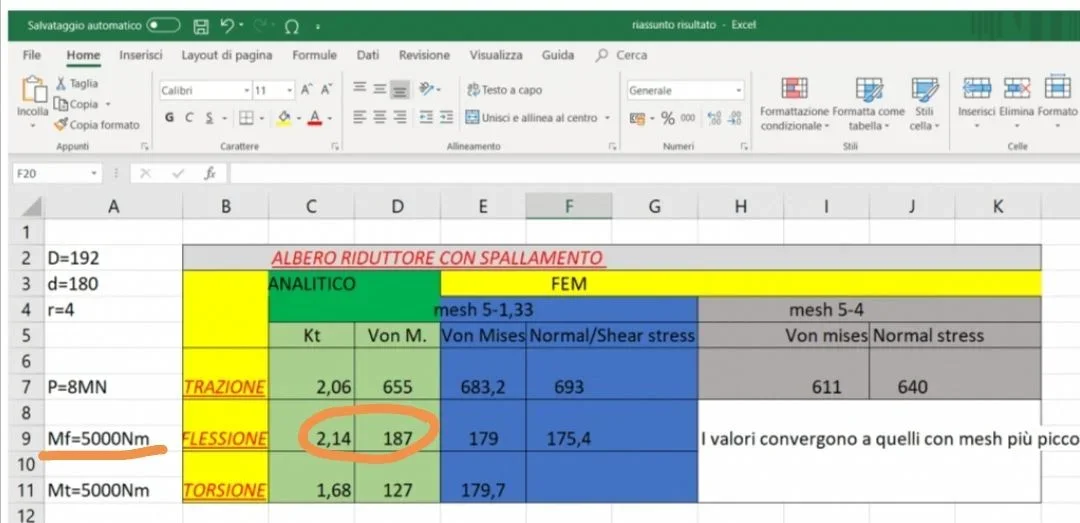
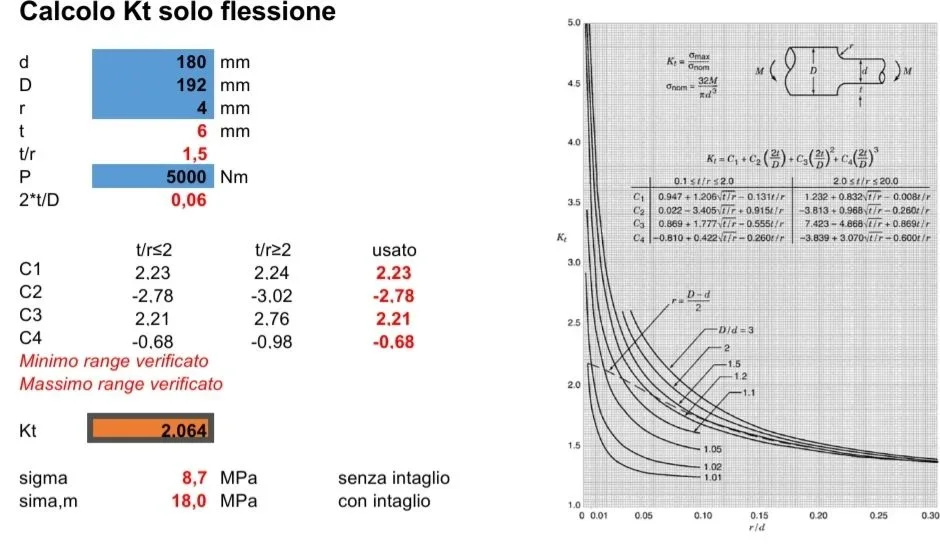
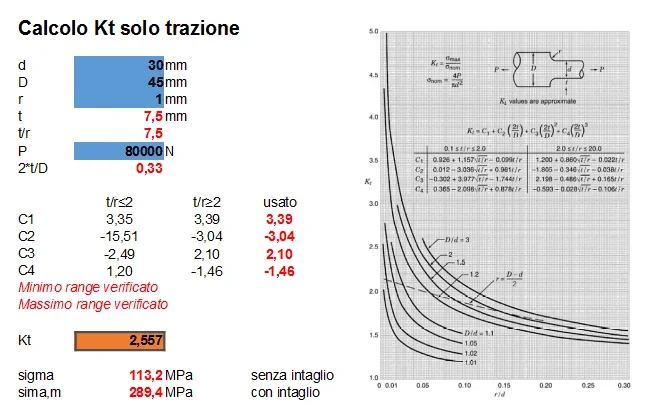
I can't understand, if each action has to be applied one at a time, as it is possible to have 300mpa tensions and kt coefficients greater than 2.
I must have missed something.
I don't really get your result. you have 300mpa but I would say it's wrong.
If you only have a torque moment, you only have 35.6mpa of tension that is what is also calculated by hand with the theoretical formula.
I took the tree where every diameter is 3 times long, so that it has a homogeneous behavior.
analyzing von mises, which is the most traditional approach that can be done, one has that the theoretical value tension is correct and one can read it quietly on the stretch 3 times the diameter.
 in the zone of the radius of 1 mm I made a mesh that divides in 4 the radius and the maximum value turns out to be 54.2mpa that is the tension that we expect on the connection radius.
in the zone of the radius of 1 mm I made a mesh that divides in 4 the radius and the maximum value turns out to be 54.2mpa that is the tension that we expect on the connection radius.the same assessment was made by evaluating the main stress:
 also here we have an intensification of the main tension that from zero passes to 60.1mpa which is the localized traction.
also here we have an intensification of the main tension that from zero passes to 60.1mpa which is the localized traction.I can't understand, if each action has to be applied one at a time, as it is possible to have 300mpa tensions and kt coefficients greater than 2.
I must have missed something.