meccanicamg
Guest
Here we are with a question that I need to solve.
I am preparing an excel sheet for calculating a pair of external cylindrical wheels and I am using the ansi/agma 2101-d04 metric standard. to say the truth I have also consulted the previous agma and the din 3990 but history changes radically.
with the term y is indicated for the Americans the form factor that is not the factor of lewis, so says the norm and is less than 1.
I had the values calculated by kisssoft and I'm sure they're inconfutable. I can't count by hand.
♪
♪
mn=6
pressure angle = 20°
helical angle = 12°
interasse = 270mm
x1=+0,41730 profile shift with present subtitles
x2=+0,13268 profile shift
provided that I still have to find to correctly calculate the parable of lewis, I used thickness and height of the tooth in the critical section with the base beams of the tooth obtained from kisssoft.
with the following formula I come y1=2,96 al post di y1=0,596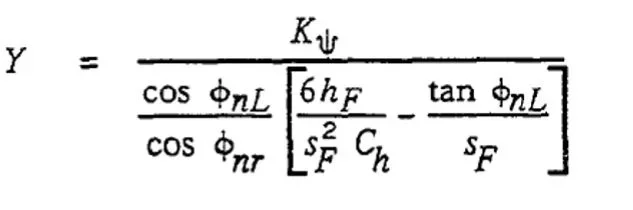 and should be like this:
and should be like this: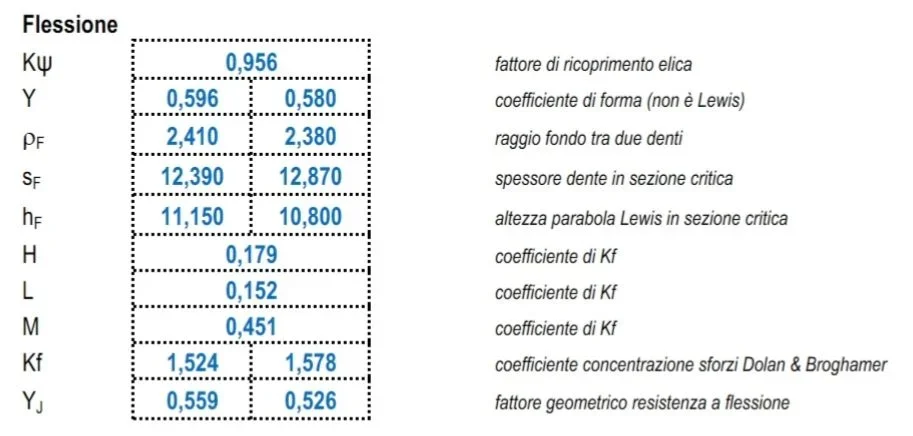 Can anyone help me out, please?
Can anyone help me out, please?
already in the formulas of kf I found that in a norm the radiants and other degrees are used.... Who knows that's something trivial. . .
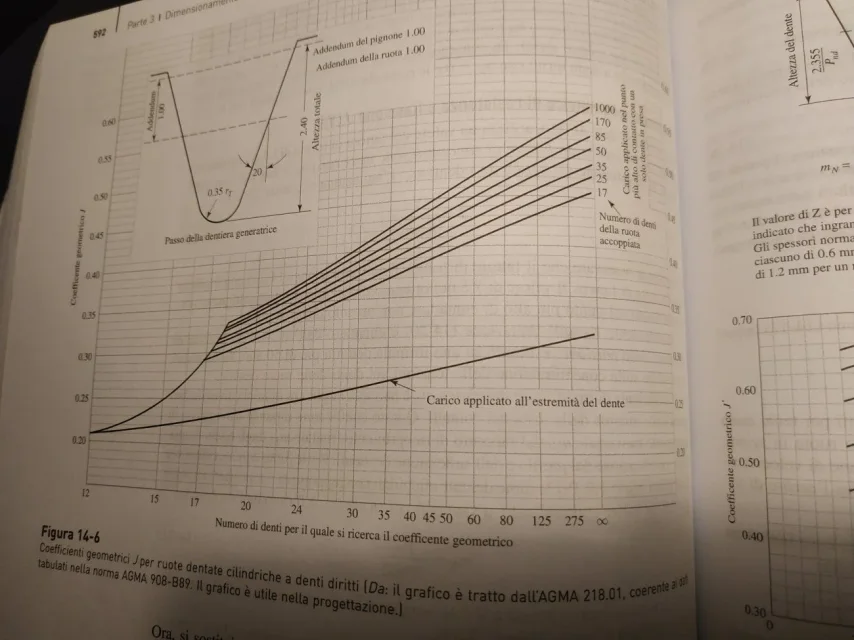
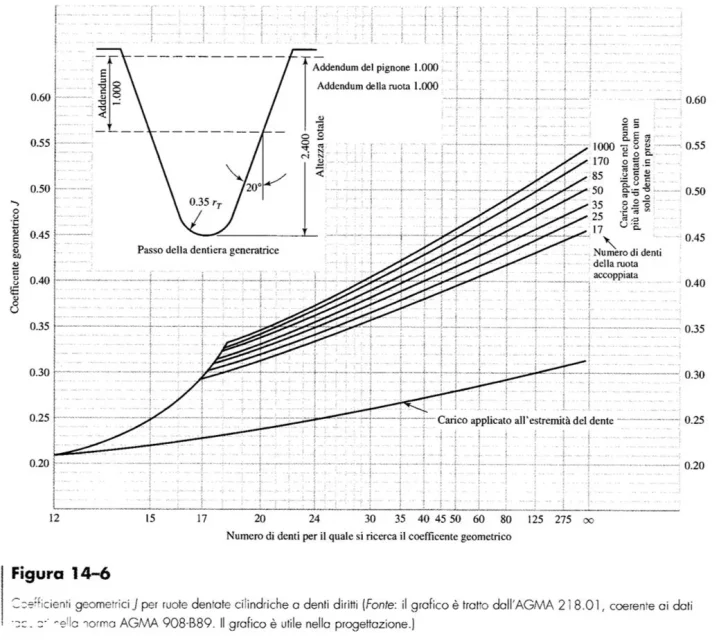
other formula provides me y1=0,418 but still we are not: Of course, for geometry, I'm using agma-908-b89, but it's not that I'm getting out of it a lot.
Of course, for geometry, I'm using agma-908-b89, but it's not that I'm getting out of it a lot.
I am preparing an excel sheet for calculating a pair of external cylindrical wheels and I am using the ansi/agma 2101-d04 metric standard. to say the truth I have also consulted the previous agma and the din 3990 but history changes radically.
with the term y is indicated for the Americans the form factor that is not the factor of lewis, so says the norm and is less than 1.
I had the values calculated by kisssoft and I'm sure they're inconfutable. I can't count by hand.
♪
♪
mn=6
pressure angle = 20°
helical angle = 12°
interasse = 270mm
x1=+0,41730 profile shift with present subtitles
x2=+0,13268 profile shift
provided that I still have to find to correctly calculate the parable of lewis, I used thickness and height of the tooth in the critical section with the base beams of the tooth obtained from kisssoft.
with the following formula I come y1=2,96 al post di y1=0,596
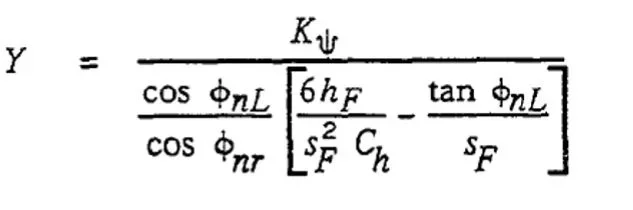 and should be like this:
and should be like this: Can anyone help me out, please?
Can anyone help me out, please?already in the formulas of kf I found that in a norm the radiants and other degrees are used.... Who knows that's something trivial. . .
other formula provides me y1=0,418 but still we are not:
 Of course, for geometry, I'm using agma-908-b89, but it's not that I'm getting out of it a lot.
Of course, for geometry, I'm using agma-908-b89, but it's not that I'm getting out of it a lot.