Treten Sie dem Forum für Designer bei!
Ihr Fachwissen ist wichtig für die Gemeinschaft. Helfen Sie uns und bringen Sie Ihr Wissen ein!
Jetzt dem Forum beitretenTauschen Sie sich aus, lernen Sie und wachsen Sie mit den besten Fachleuten der Branche.
Zusammenfassung
Im ersten Teil dieser Diskussionsreihe untersuche und überprüfe ich die Beziehung zwischen Handberechnungen und der zeitabhängigen Reaktion eines Objekts, das auf eine starre Oberfläche fällt, und welche Verformungen und Spannungen während dieser Aufprallzeit auftreten. Die im Folgenden besprochenen Konzepte sind unerlässlich, um zu verstehen, wie man eine instationäre Strukturanalyse mit ANSYS Mechanical einrichtet und löst.
Abbildung 1: Balken beim Aufprall (mit übertriebener Durchbiegungsskala).
Abbildung 1 veranschaulicht unsere Beispielstange nach dem Fallenlassen und zeigt, was während des Aufpralls passiert. Der restliche Teil des Dokuments befasst sich damit, wie wir diese Art von System einrichten und analysieren und unsere Fortschritte mit den üblichen Berechnungen von Hand vergleichen können.
Hier ist eine Liste der Themen, die in dieser Diskussion behandelt werden (in der Reihenfolge ihres Erscheinens):
- Potentielle Energie
- Elastische Energie
- Gerichtete Steifigkeit
- Statische Strukturanalyse
- Durchschnittliche Druckkraft
- Kinetische Energie
- Aufprallgeschwindigkeit
- Aufpralldauer
- Eigenfrequenz
- Modale effektive Masse
- Transiente Strukturanalyse
- Analyse Dauer
- Zeit-Schritt Frequenz
- Ergebnisse für komplexe transiente Verschiebung und Spannung
- Durchschnittliche Druckspannung
Details
Ich habe begonnen, die Beziehung zwischen manuellen Berechnungen und den Ergebnissen der maximalen Durchbiegung und Spannung bei dynamischen Ereignissen, wie dem Aufprall eines Objekts auf ein anderes, zu untersuchen. Ich habe ANSYS Mechanical verwendet, um Annahmen zu überprüfen und mehr Details über diese dynamischen Ereignisse zu erhalten. Ich habe Vertrauen in die Finite-Elemente-Methode und freue mich darauf, meine Ergebnisse mit Ihnen zu teilen.
Ich habe meine Untersuchung mit einem einfachen Beispiel eines zylindrischen Stabes begonnen, der auf eine starre Oberfläche fällt. In diesem Szenario und in allen Szenarien, die im Zusammenhang mit dieser Diskussion stehen, gehe ich von einem elastischen Materialverhalten aus und davon, dass keine der Belastungen zu Plastizität oder Schäden führt. Das bedeutet, dass die Energie innerhalb der Geometrie erhalten bleibt.
Während dieses Prozesses habe ich eine Reihe von Annahmen getroffen und Finite-Elemente-Analysen durchgeführt, um diese Annahmen entweder zu bestätigen oder zu widerlegen. Dieser Prozess veranlasste mich, weitere Fragen zu stellen, zu analysieren und weitere Antworten zu erhalten. Am Ende bin ich in der Lage, viele Aspekte dieses dynamischen Ereignisses selbstbewusst zu beschreiben, die ich alle so knapp wie möglich darstellen werde.
Lassen Sie uns mit der einfachsten Idee beginnen.
In diesem ersten Beispiel geht es um den Fall eines zylindrischen Stabes auf eine harte Oberfläche. Die Stange hat einen Durchmesser von 25,4 mm und eine Länge von 254 mm und eine Massendichte von 7,85e-06 [kg/mm³]. Diese Stange wird aus 1 Meter Höhe von der Unterseite fallen gelassen.
Abbildung 2: Zylindrischer Stab
Unter diesen Umständen muss die potentielle Energie gleich der elastischen Energie sein.
Potentielle Energie:

Elastische Energie:

Lassen Sie uns die potentielle Energie unseres fallenden Zylinders mit seiner elastischen Energie gleichsetzen, um zu erfahren, ob wir die Durchbiegungen genau vorhersagen können.
Gehen wir davon aus, dass die Stange so fallen gelassen wird, dass sie sich in negativer Y-Richtung bewegt. Der erste Schritt besteht also darin, die Steifigkeit unserer Geometrie in Y-Richtung zu bestimmen.
Für unser Modell lässt sich diese Steifigkeit sowohl theoretisch als auch mit Hilfe der Finite-Elemente-Methode ableiten, bei der eine bekannte Last aufgebracht und diese Last durch die berechnete Durchbiegung in Y-Richtung geteilt wird. Auf diese Weise können wir die Ergebnisse unserer Finite-Elemente-Schätzung mit dem theoretisch abgeleiteten Wert vergleichen und Vertrauen in unsere Methodik entwickeln.
Lassen Sie uns unsere theoretische Steifigkeit ableiten. Für die Y-Richtung gilt die folgende Formel:

Lassen Sie uns nun auch die Steifigkeit der Geometrie durch eine Finite-Elemente-Analyse mit zwei verschiedenen Methoden berechnen, damit wir die unterschiedlichen Überlegungen zu den verschiedenen Arten von Belastungen verstehen.
Hier betrachten wir eine feste Basis, während wir eine Kraft auf das distale Ende unseres Zylinders ausüben, so dass die Reaktionskraft an der Basis gleich groß ist und das entgegengesetzte Vorzeichen der Kraft hat, die auf die Oberseite des Zylinders wirkt. Die Größe dieser Druckkraft ist nicht entscheidend, solange unsere Materialeigenschaften linear sind und wir keine geometrische Nichtlinearität (große Verformung) berücksichtigen.
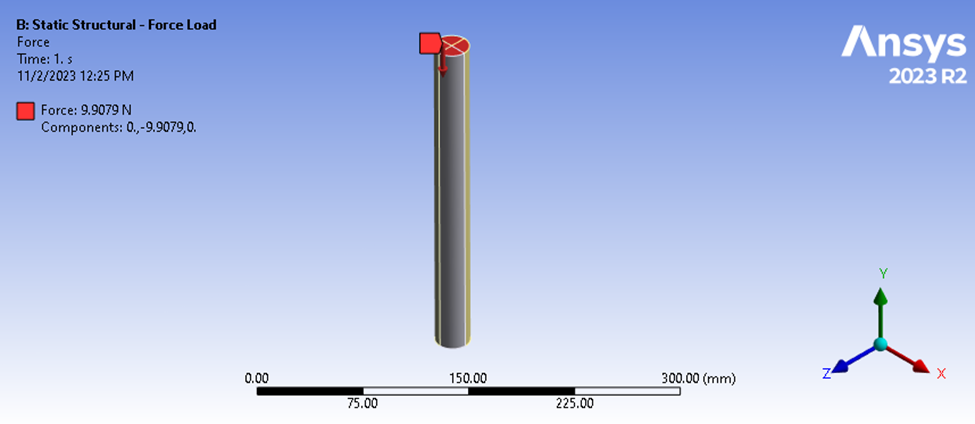
Abbildung 3: Statische Strukturanalyse des Stabes, der von oben belastet wird und an der Unterseite abgestützt ist.
In diesem Szenario wird eine Last von 9,9079 N auf die Oberseite aufgebracht, während die Unterseite durch Y-Verschiebungen fixiert ist. Die Größe dieser Belastung wird später noch deutlicher werden.
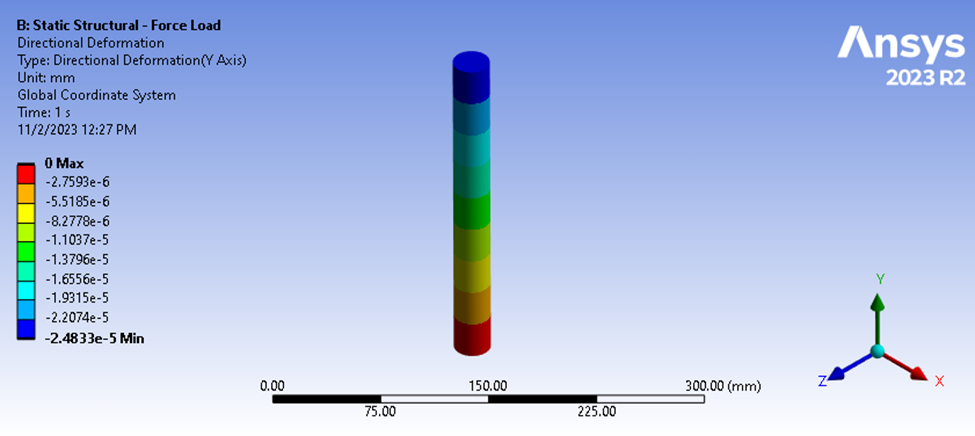
Abbildung 4: Ergebnisse der statischen Strukturverformung
Die Lösung der statischen Strukturanalyse zeigt eine maximale Größe für unsere Druckverformung von 2,4833e-5 mm. Ausgehend von unserer Last von 9,9079 N können wir die folgende durchschnittliche Steifigkeit berechnen.
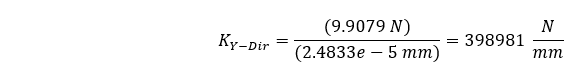
Man sieht, dass der Finite-Elemente-Ansatz nur 0,00125% Unterschied zum theoretischen Ansatz aufweist. Das gibt uns ein gutes Gefühl 😊.
Betrachten wir als nächstes eine andere Art der Belastung, z.B. die Schwerkraftbelastung. Hier wird die Kraft von der Oberseite genommen, aber die Unterseite bleibt eingespannt, und die Schwerkraft wirkt mit 9806,6 mm/sec^2. Die Reaktionskraft an der Unterseite beträgt 9,9079 N, aber die Kraft, die auf die Oberseite wirkt, ist definitiv Null. Die Ergebnisse der Durchbiegung zeigen eine unterschiedliche Größe der Durchbiegung von 1,2421e-5 mm.
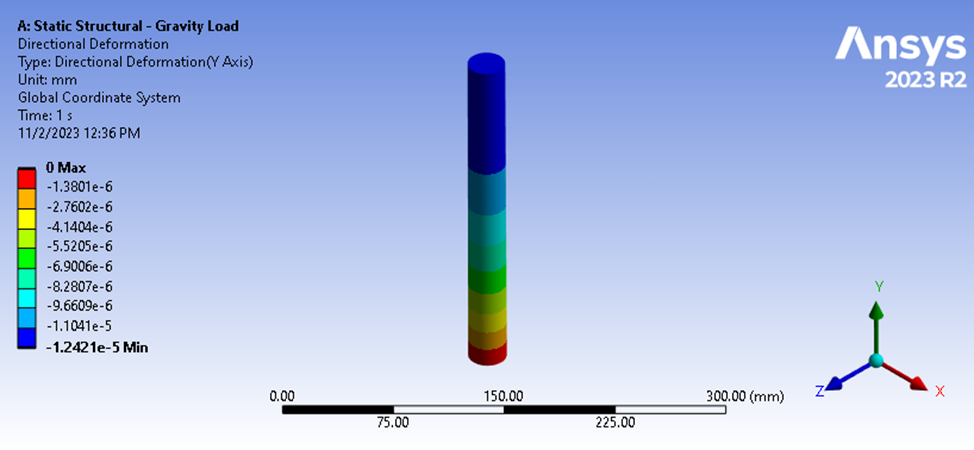
Abbildung 5: Ergebnisse der statischen Strukturanalyse – Durchbiegung
Wenn wir versuchen würden, die Steifigkeit mit der gleichen Form der Gleichung wie oben zu berechnen, kämen wir zu einem falschen Wert, da wir die durchschnittliche Druckkraft, die durch unsere Geometrie wirkt, nicht berücksichtigen würden. In diesem Fall kann die durchschnittliche Druckkraft leicht abgeschätzt werden, da unsere Geometrie einen konstanten Querschnitt hat. Die geschätzte durchschnittliche Steifigkeit kann wie folgt berechnet werden.
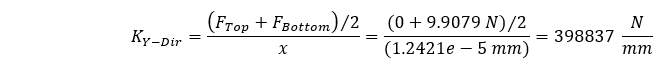
Diese Schätzung zeigt eine Abweichung von 0,0348% von unserem theoretisch berechneten Wert. Daher können wir mit zwei verschiedenen Belastungsmethoden die Steifigkeit der Geometrie in Richtung des Querschnitts zuverlässig schätzen.
Wenn wir unsere geschätzte Richtungssteifigkeit zusammen mit unserem Modell und den Materialeigenschaften einsetzen, können wir die maximale Durchbiegung wie folgt schätzen.
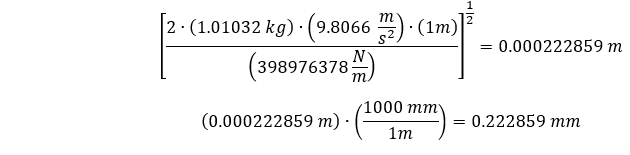
Das sind etwa ~0,223 mm. Nun benötigen wir ein instationäres Strukturmodell, um die Durchbiegungen beim und nach dem Aufprall unseres zylindrischen Stabs auf den Boden zu simulieren.

Abbildung 6: Transientes Strukturanalysemodell und Beschränkungen
Unser Modell geht davon aus, dass sich die Stange mit 4428 mm/s in negativer Y-Richtung bewegt. Dies ist die Geschwindigkeit, die die Stange erreichen würde, wenn sie 1 m tief fallen würde. Wir können dies berechnen, indem wir die potentielle Energie der Welle mit ihrer kinetischen Energie zum Zeitpunkt des Aufpralls gleichsetzen.
Kinetische Energie:
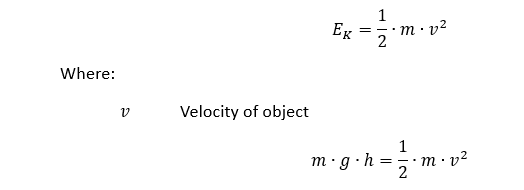
Daher:

Es werden Einschränkungen hinzugefügt, um die vertikale Statur der Geometrie beizubehalten, während der Basis eine reine Druckstütze hinzugefügt wird. Die Analysedauer wird festgelegt (mehr dazu später), ebenso wie eine häufige Erfassungsrate für die Erfassung der Ergebnisse.
Die Analyseergebnisse sind kompliziert, denn während sich der obere Teil des Stabes nach dem Aufprall nach unten biegt, kann der untere Teil des Stabes aufgrund der Steifigkeit der reinen Druckstütze leicht zusammengedrückt werden. Der Unterschied in der Durchbiegung zwischen diesen beiden Flächen beschreibt die Gesamtkompression der Stange.
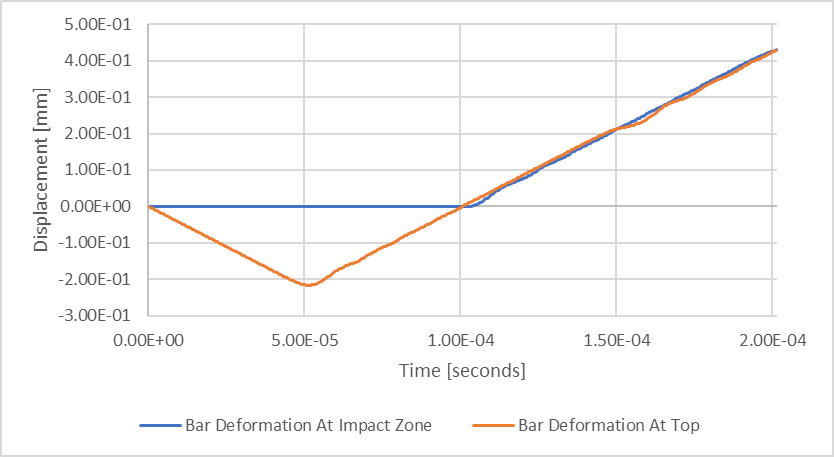
Abbildung 7: Ergebnisse der instationären strukturellen Durchbiegung
Die flache Periode der blauen Linie, „Bar Deformation at Impact Zone“, zeigt die Periode, in der der Kontakt an der Basis stattfindet, oder die Verweildauer im Zusammenhang mit dem Aufprall. Wenn wir unsere Daten neu aufzeichnen, um uns auf diesen Zeitraum zu konzentrieren, können wir leichter mehrere Beobachtungen machen.
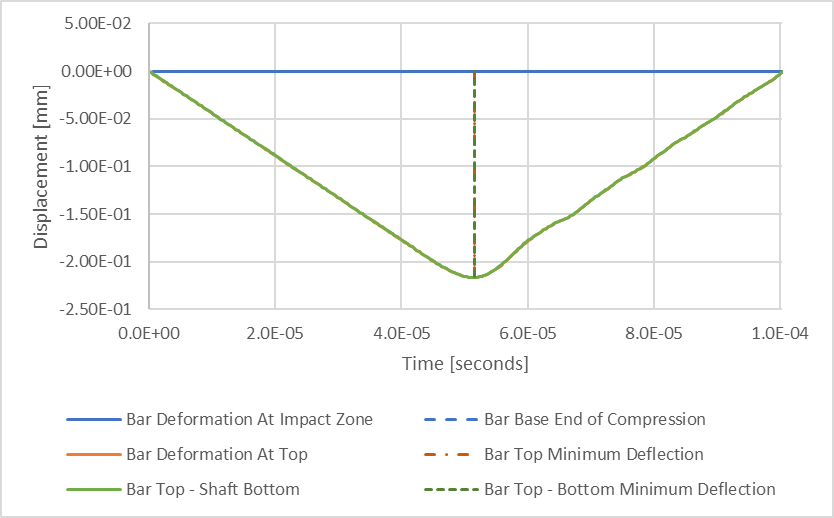
Abbildung 8: Ergebnisse der transienten strukturellen Druckverformung
Ich habe eine grüne Linie hinzugefügt, die die Differenz zwischen der Durchbiegung der Ober- und der Unterseite des Balkens darstellt, was die Gesamtkompression des Balkens in Abhängigkeit von der Zeit ergibt. Die beiden vertikalen gestrichelten Linien stellen die Zeitintervalle dar, die mit den minimalen Ergebnissen der orangen und grünen Linien verbunden sind. Sie sehen, dass die minimale Kompression des Balkens zur gleichen Zeit auftritt wie die minimale Kompression der Oberseite des Balkens. Daraus können wir ableiten, dass die maximale Kompression unseres Balkens 0,216 mm beträgt, was knapp 3 % weniger ist als unsere geschätzte maximale Durchbiegung von 0,223 mm.
Es gibt jedoch noch mehr zu entdecken und aus diesem Beispiel und seinen Ergebnissen zu lernen.
Lassen Sie uns nun den Aspekt der Erstellung einer instationären Strukturanalyse betrachten und uns speziell mit der Zeitspanne befassen, die mit unserem Ereignis verbunden ist, und feststellen, wie wir diese Zeitspanne für eine beliebige Geometrie abschätzen können.
Betrachten wir den Zeitpunkt, an dem die blaue Linie von einer negativen Verschiebung zu einer positiven Verschiebung überging (0,00010026 Sekunden), was der Zeitspanne entspricht, die mit der Kompression unserer Welle verbunden ist.
Unsere Welle kann als eine Feder betrachtet werden, die zurückfedert. Die Dauer des Aufpralls entspricht ½ der Periode ihrer Eigenfrequenz in Richtung der Kompression. Daher sollte das Folgende wahr sein.

Lassen Sie uns nun untersuchen, ob wir diese Theorie unterstützen können und wie wir die Eigenfrequenz für diese und alle anderen Geometrien, die wir in Zukunft zu analysieren hoffen, abschätzen können.
Wir können die auf das obige Testmodell angewendete „Nur-Druck“-Unterstützung mit einer Y-Richtungs-Beschränkung auf denselben Flächen ändern und direkt für unsere Längsschwingungsfrequenz in ANSYS lösen.
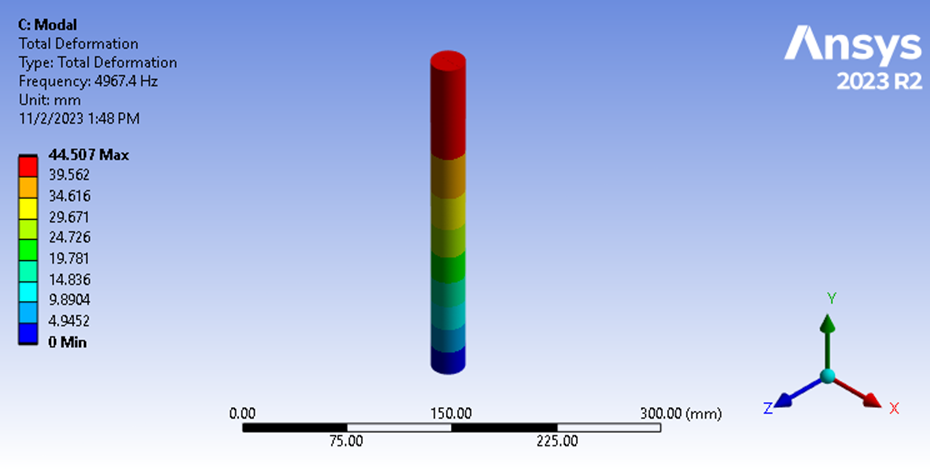
Abbildung 9: Modalanalyse Grundfrequenz
Hier sehen wir, dass die Längsschwingungsfrequenz 4967,4 Hz beträgt. Dies zeigt, dass unsere Schätzung der Eigenfrequenz auf der Grundlage der Ergebnisse der instationären Strukturverschiebung mit einer Genauigkeit von 0,4 % richtig war. Dieses Ergebnis bestätigt unsere Theorie, dass die Dauer des Aufpralls gleich ½ der Periode der Grundfrequenz für die weichere der beiden aufprallenden Objekte ist.
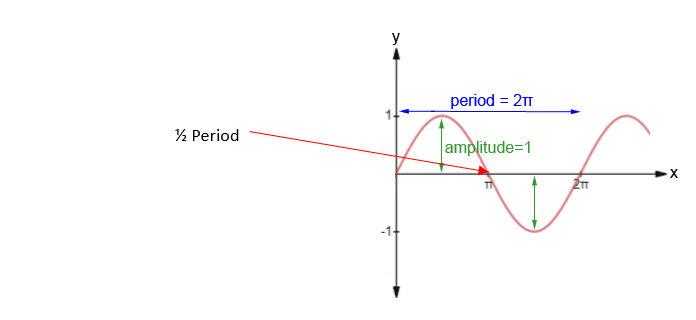
Abbildung 10: Aufpralldauer
In unserer Beispielanalyse haben wir nur ein Teil und nehmen an, dass die vertikale Stütze, die nur auf Druck belastet wird, ein weiteres sehr steifes Objekt darstellt. Daher ist unsere Welle der flexiblere der beiden Stoßpartner. Unsere instationäre Strukturanalyse wurde so definiert, dass die Analysedauer gleich der Periode dieser Eigenfrequenz ist, und wir erwarten, dass der Aufprall während der ersten ½ dieser Periode stattfindet.
Aber wie berechnen wir diese Eigenfrequenz, wenn wir eine instationäre Strukturanalyse aufstellen?
Wir können so vorgehen, wie ich es gerade demonstriert habe, d.h. eine Modalanalyse der Geometrie durchführen und dabei Einschränkungen verwenden, um die Aufprallhaltung beizubehalten, und direkt die Modenform der Aufprallkompression lösen. Aber gibt es einen analytischen Weg, um das Gleiche zu erreichen?
Um dies herauszufinden, müssen wir die Eigenfrequenz unserer Geometrie in der Aufprallrichtung berechnen, die wie folgt berechnet werden kann.

Wir haben bereits untersucht, wie wir die richtungsabhängige Steifigkeit abschätzen können, aber lassen Sie uns jetzt ein paar Beispiele betrachten, um die Berücksichtigung der modalen effektiven Masse besser zu verstehen.
Die Gesamtmasse unseres Systems ist:
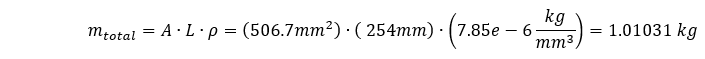
Die effektive Masse unseres Systems wird geringer sein als die Gesamtmasse, da ein Ende unserer Geometrie eingeschränkt ist. Je nach Komplexität unserer Geometrie und der Einschränkungen, die wir zur Fixierung der Geometrie verwenden, kann es schwierig sein, die Menge der Masse abzuschätzen, die daran beteiligt sein wird. In unserem Fall ist die Geometrie einfach und für extrudierte Querschnitte, die an einem Ende fixiert sind, wird die effektive Masse oft mit 1/3 der Gesamtmasse des Systems gleichgesetzt. Wenn dies der Fall wäre, dann wäre unsere Grundfrequenz die folgende:
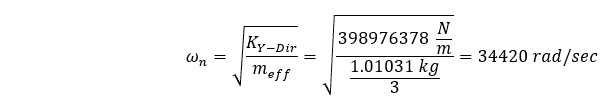
Sie lässt sich besser erkennen, wenn man sie wie folgt ausdrückt:
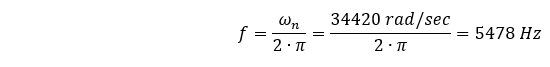
Dieser Wert (5478 Hz) ist über 10% größer als unsere mit der Finite-Elemente-Methode berechnete Eigenfrequenz (4967,4 Hz)… warum?
Die Antwort hängt mit der Schätzung der modalen effektiven Masse zusammen. Wenn wir uns bei der Berechnung der Längssteifigkeit sicher sind (…sind wir…), dann können wir unser Modell ändern, um die Berechnung unserer Grundfrequenz leichter zu überprüfen.
Wir setzen die Massendichte unseres Materials für unser Modell auf Null und fügen dem distalen Ende unserer Geometrie eine Masse von 1,01031 kg hinzu, was die folgende Eigenfrequenz ergeben sollte.
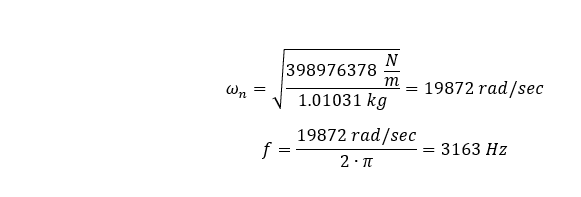
Nachdem wir die Finite-Elemente-Analyse durchgeführt haben, sehen wir, dass die longitudinale Grundfrequenz 3154,6 Hz beträgt.
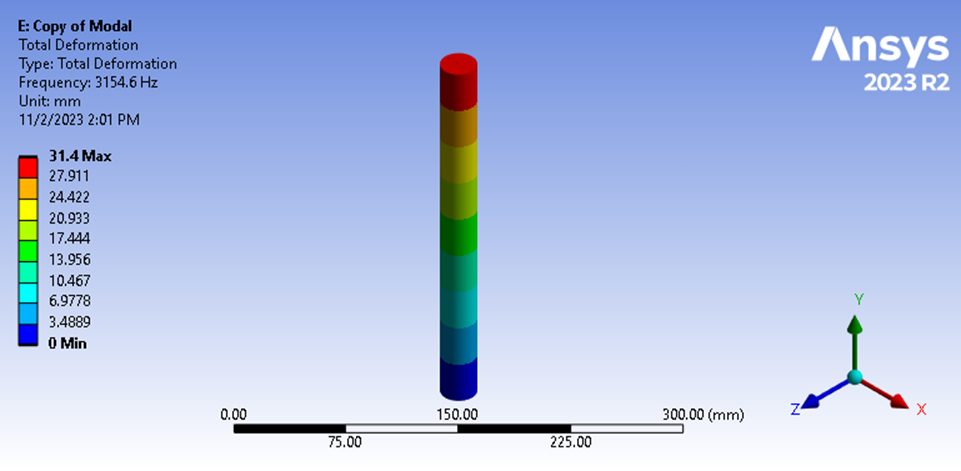
Abbildung 11: Modalanalyse Grundfrequenz
Dies entspricht einer Abweichung von 0,27% von unserer Handberechnung. Daher entwickeln wir mehr Vertrauen in die Finite-Elemente-Methode und stellen eine Schwäche in unserer Schätzung der effektiven Masse fest, die wir in unserer Handberechnung verwendet haben, indem wir die Masse über unsere Geometrie verteilt haben.
Indem wir unsere Gleichung umstellen, können wir diese effektive Masse unter Berücksichtigung der von ANSYS berechneten Eigenfrequenz und unter Berücksichtigung der verteilten Masse wie folgt lösen:
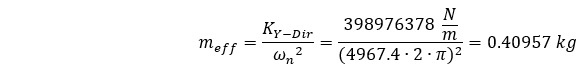
Wir stellen fest, dass diese effektive Masse 0,405 der Gesamtmasse des Systems beträgt.
Daher können wir davon ausgehen, dass dieser Massenanteil für andere und komplexere Geometrien einzigartig und theoretisch schwierig abzuleiten ist und dass wir die Eigenfrequenz mit der Finite-Elemente-Methode zuverlässig lösen können.
Da wir nun wissen, wie wir die Eigenfrequenz für eine bestimmte Geometrie bestimmen, müssen wir festlegen, bei welcher Frequenz wir die Analyseergebnisse während unserer instationären Analyse erfassen sollen.
Dazu sollten wir uns überlegen, wie sich die Größe der Analyseschritte aus zwei verschiedenen Perspektiven auf die Analyse auswirkt. Die eine Perspektive bezieht sich auf das, was man bei einer stückweisen linearen Charakterisierung einer nichtlinearen Reaktion, wie z.B. einer Sinuswelle, erwarten könnte. Die andere Perspektive bezieht sich darauf, wie sich die tatsächlichen Analyseergebnisse in Abhängigkeit von der Änderung der Erfassungsratenfrequenz verändern. Da wir ein Aufprallproblem betrachten und davon ausgehen, dass die Aufprallperiode mit der Grundschwingung unserer flexiblen Komponente zusammenhängt, ist es sinnvoll, die Beziehung zwischen der Schrittgröße und deren Auswirkungen auf die Genauigkeit der Darstellung einer Sinuskurve zu untersuchen.
Um diese Beziehung zu bewerten, vergleichen wir den gewichteten Mittelwert des Betrags für die erste Hälfte der Sinuskurve mit dem theoretischen Mittelwert der gleichen Spanne, der gleich ist:
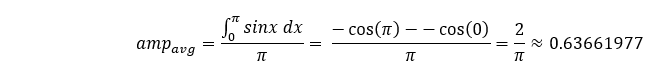
Jetzt untersuchen wir, wie genau wir diese Sinuskurve mit einer anderen Anzahl von Schritten darstellen. Dann verwenden wir die Trapezregel, um die Fläche unter der Kurve für die erste Hälfte zu berechnen, und dividieren diese Fläche durch die Periode dieser Spanne.
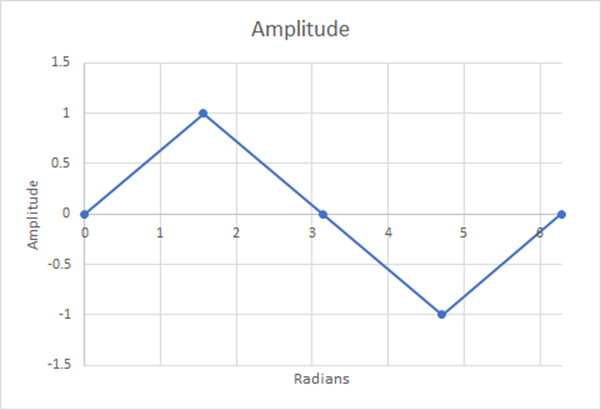
Abbildung 12: 4 Schritte; geschätzter gewichteter Mittelwert=0,5; 21,46% Abweichung
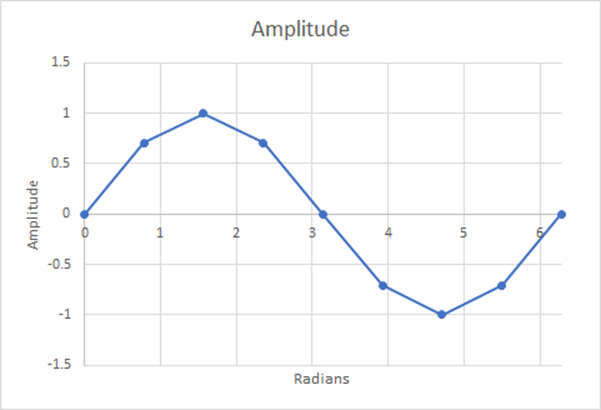
Abbildung 13: 8 Schritte; geschätzter gewichteter Mittelwert=0,60536; 5,19% Abweichung
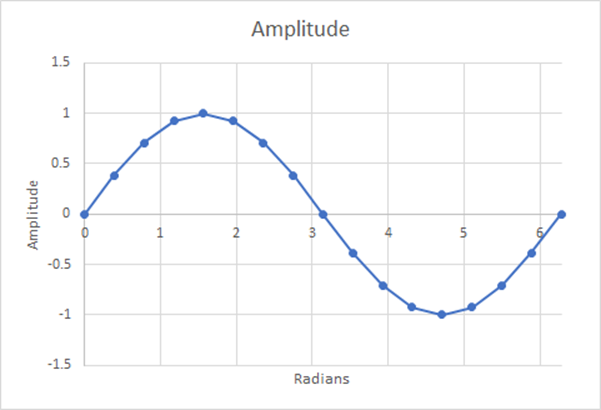
Abbildung 14: 16 Schritte; geschätzter gewichteter Mittelwert=0,6284; 1,29% Abweichung
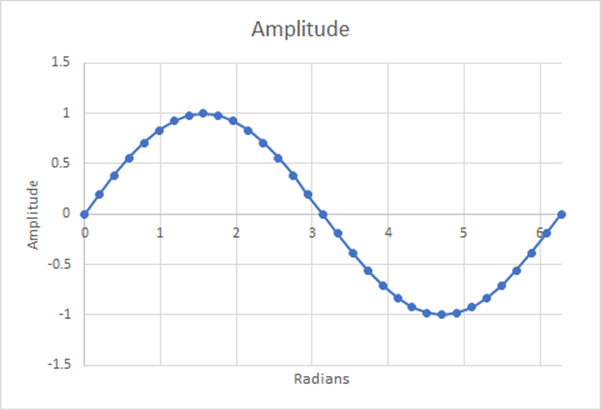
Abbildung 15: 32 Schritte; geschätzter gewichteter Mittelwert=0,6346; 0,32% Abweichung
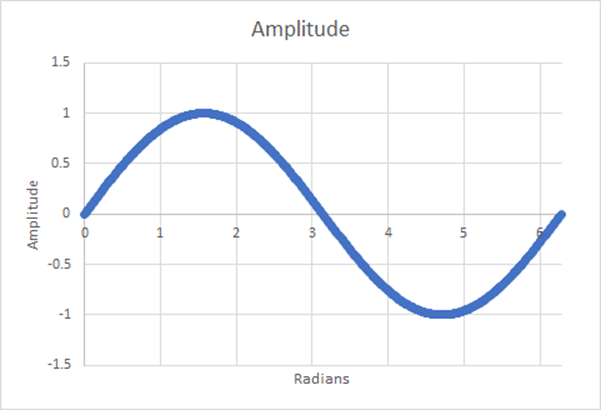
Abbildung 16: 512 Schritte; geschätzter gewichteter Mittelwert=0,6366; 0,001% Abweichung
Tatsächlich erreichen wir nie eine perfekte Übereinstimmung mit dem theoretischen Wert, und wir können aufzeichnen, wie sich diese Genauigkeit mit zunehmender Anzahl der Zeitschritte verändert, wie unten dargestellt.
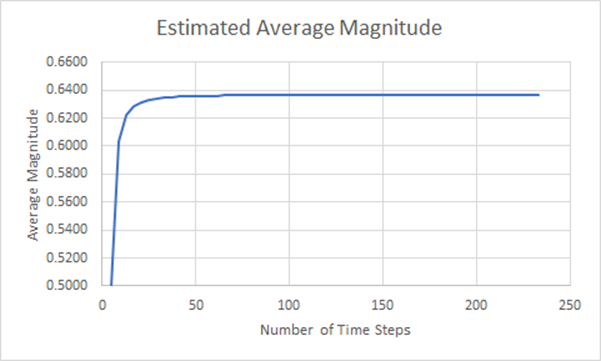
Abbildung 17: Konvergenzdiagramm für die geschätzte durchschnittliche Magnitude
Anhand dieser Untersuchung können wir erkennen, dass die Genauigkeit schnell zunimmt, wenn wir die Anzahl der Schritte in unserer Näherung erhöhen. Dabei wird jedoch nicht berücksichtigt, wie sich die Ergebnisse entwickeln, wenn die Anzahl der Zeitschritte erhöht wird.
Um den Einfluss auf die Analyseergebnisse zu untersuchen, werden wir unsere Ergebnisse der maximalen Stabkompression als Funktion der Zeit darstellen, während wir verschiedene Anzahlen von Zeitschritten in der Lösung berücksichtigen.
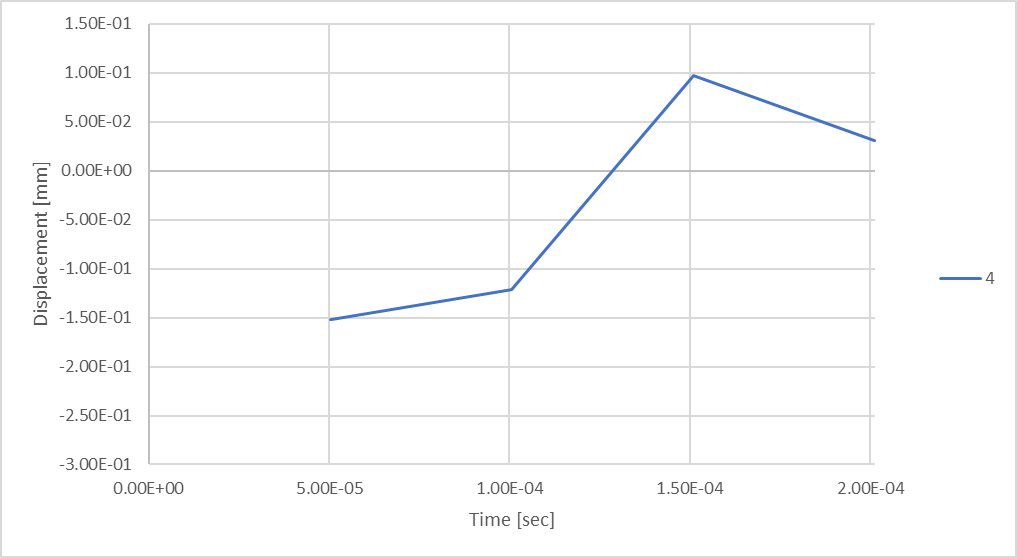
Abbildung 18: Stabverschiebung bei Berücksichtigung von 4 Zeitschritten.
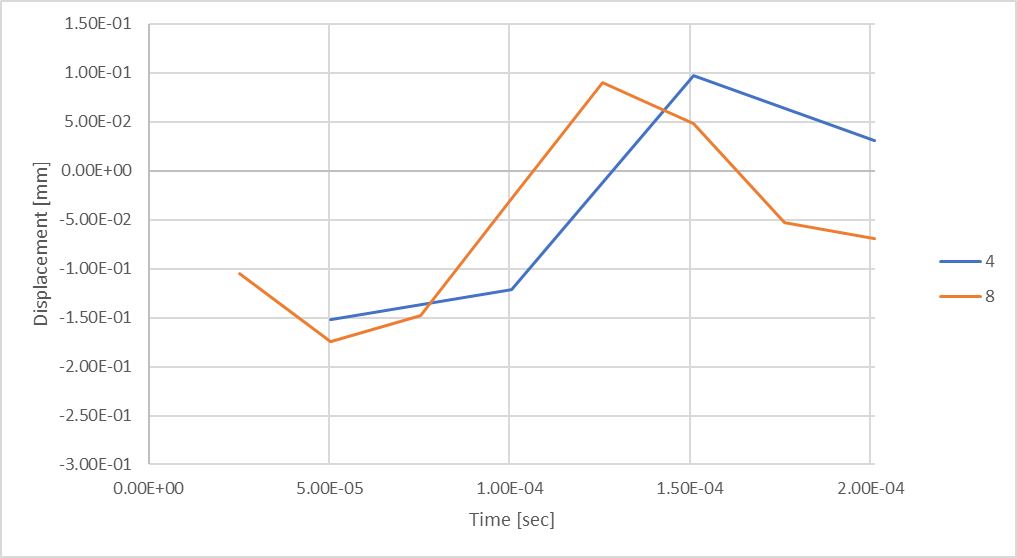
Abbildung 19: Stabverschiebung bei Berücksichtigung von 8 Zeitschritten.
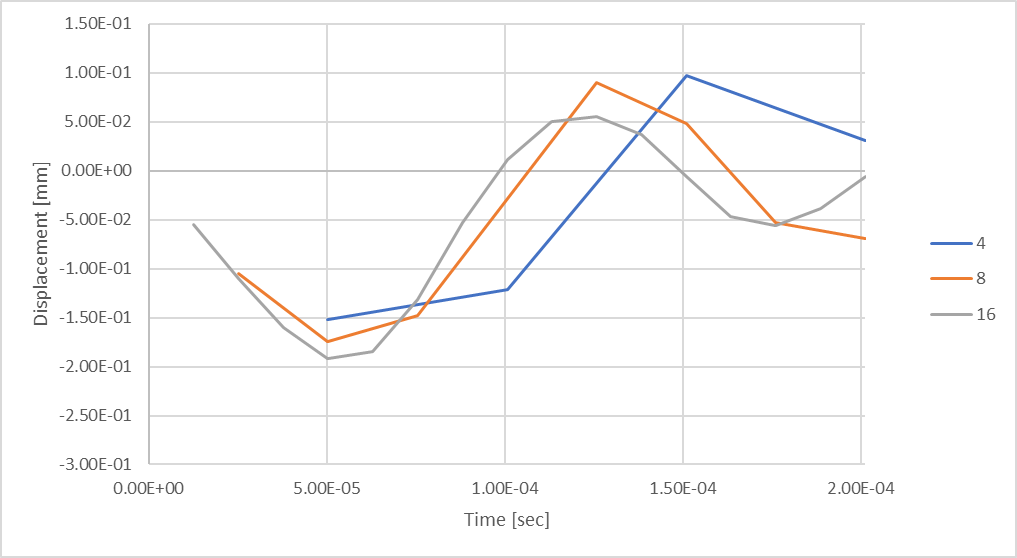
Abbildung 20: Bei 16 Zeitschritten sehen wir größere Druckverschiebungen der Stäbe.
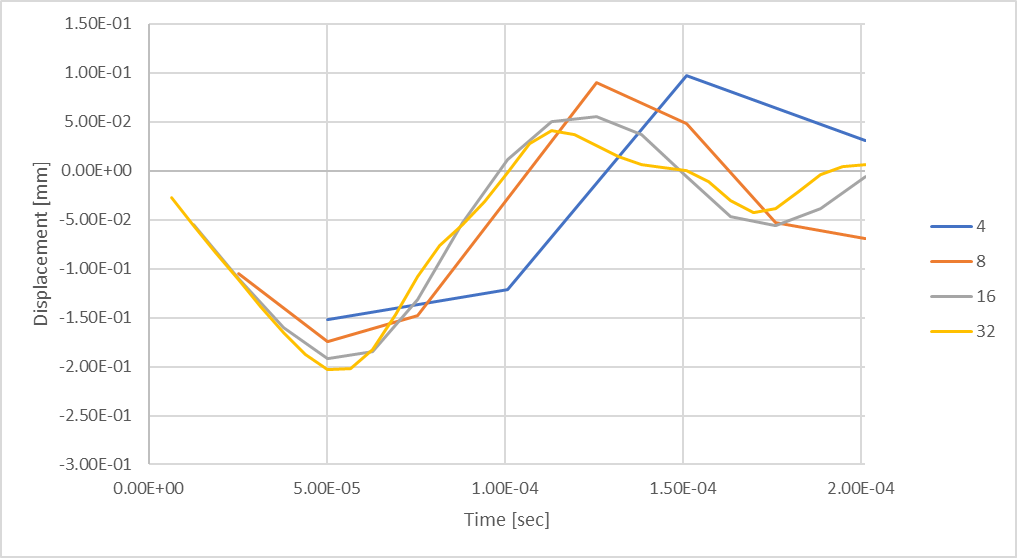
Abbildung 21: Vorübergehende maximale Stabverbiegung bei 32 Zeitschritten.
Auf der Grundlage unserer vorherigen Analyse zur Berechnung der durchschnittlichen sinusförmigen Größe haben wir festgestellt, dass wir bei der Berücksichtigung von 32 Schritten mit einer Abweichung von bis zu 0,32 % von den theoretischen Ergebnissen rechnen sollten. Wir können jedoch sehen, dass sich unsere Reaktion auf die Druckverschiebung des Stabes im Vergleich zu den vorherigen Untersuchungen mit Zeitschritten immer noch bildet. Was passiert, wenn wir zusätzliche Zeitschritte berücksichtigen?
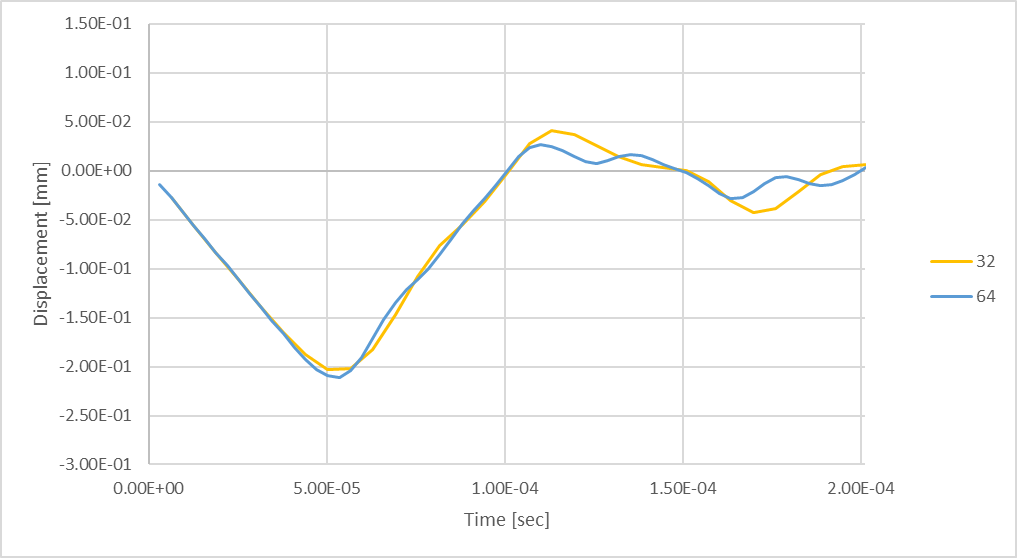
Abbildung 22: Einschwingende maximale Stabdurchbiegung mit 64 Zeitschritten.
64 Zeitschritte führen zu einer geringfügig größeren, aber größtenteils ähnlichen maximalen Durchbiegung der Stange. Allerdings gibt es Anzeichen für die Entwicklung höherfrequenter Schwingungen während des Rückpralls der Stange.
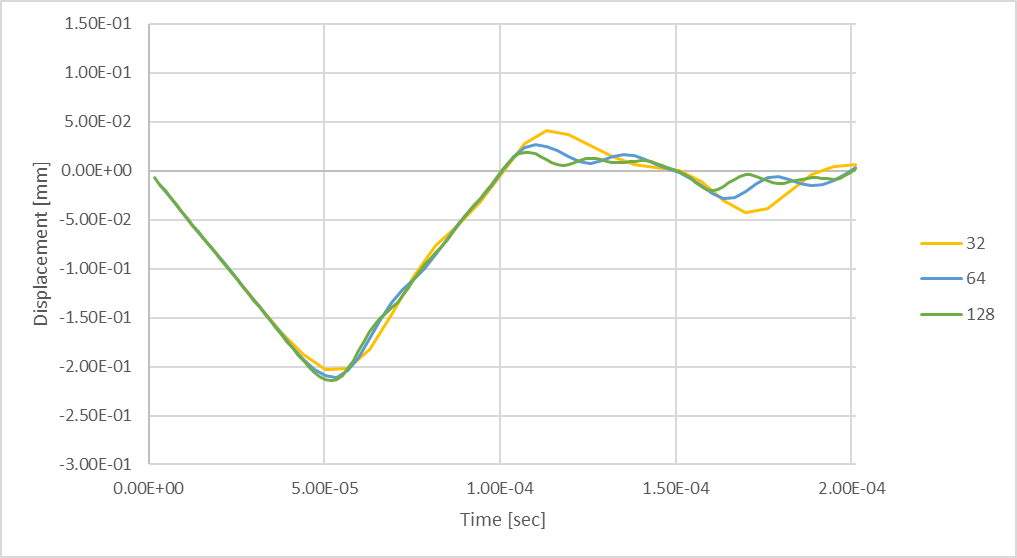
Abbildung 23: Einschwingende maximale Stabdurchbiegung mit 128 Zeitschritten.
Die Berücksichtigung von 128 Zeitschritten führt zu einer größeren Spitzendruckkraft in der Welle als die geringere Anzahl von Zeitschritten. Die maximale Druckverformung ist 6 % größer als bei der Berücksichtigung von 32 Zeitschritten.
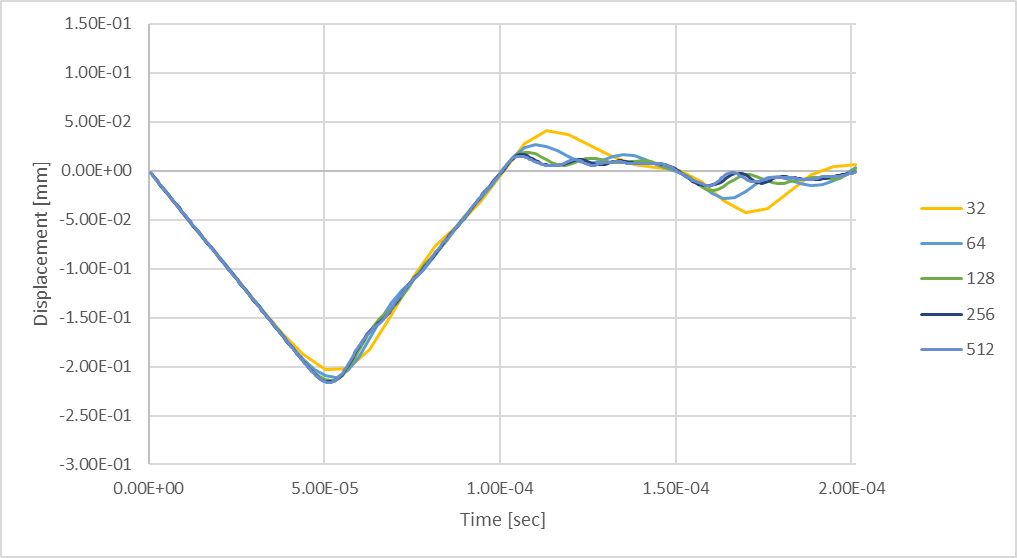
Abbildung 24: Einschwingende maximale Stabdurchbiegung bei Verwendung von bis zu 512 Zeitschritten.
Der Vergleich der Analyseergebnisse mit 256 Zeitschritten mit den Ergebnissen, die sich bei Berücksichtigung von 512 Zeitschritten ergeben, zeigt, dass durch die Berücksichtigung von mehr Zeitschritten eine weitere Auflösung der dynamischen Reaktion berechnet werden kann. Das folgende Diagramm veranschaulicht, wie sich unsere maximalen Druckstabverformungen in Abhängigkeit von der Anzahl der in einer instationären Strukturanalyse berücksichtigten Zeitschritte verändern werden.
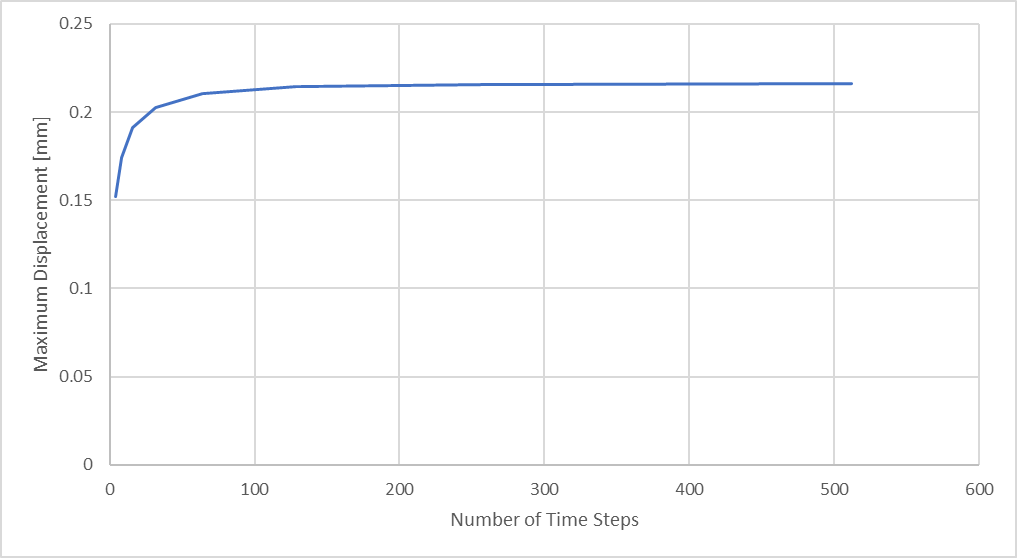
Abbildung 25: Maximale Stangendruckverschiebung in Abhängigkeit von der Anzahl der Analysezeitschritte
Schließlich erreichen wir bei einer bestimmten Netzgröße einen Punkt, an dem der Aufwand für eine längere Analysezeit und größere Ergebnisdateien nicht mehr durch eine signifikante Veränderung der Ergebnisgröße gerechtfertigt ist.
Anhand dieser beiden Überlegungen sehen wir, dass wir bei Verwendung von 32 Zeitschritten eine Sinuskurve mit einer Abweichung von bis zu 0,32% charakterisieren können, aber im Vergleich zur gleichen Analyse mit 512 Zeitschritten nur Ergebnisse mit einer Genauigkeit von 94% und im Vergleich zu unserer theoretischen maximalen Durchbiegung nur eine Genauigkeit von 91% erzielen können. In der Abbildung unten sehen Sie, wie unsere Ergebnisse für die maximale Stauchung der Stange im Vergleich zu unserem theoretisch geschätzten Maximum ausfallen.
| Anzahl von Teilschritten | Maximale Komprimierung | Theoretische Max | % Abweichung |
| 4 | 0.152139 | 0.222859 | 31.73% |
| 8 | 0.174023 | 0.222859 | 21.91% |
| 16 | 0.191486 | 0.222859 | 14.08% |
| 32 | 0.202746 | 0.222859 | 9.03% |
| 64 | 0.210712 | 0.222859 | 5.45% |
| 128 | 0.214455 | 0.222859 | 3.77% |
| 256 | 0.215752 | 0.222859 | 3.19% |
| 512 | 0.216232 | 0.222859 | 2.97% |
Abbildung 26: Maximale Druckverschiebung des Stabes im Vergleich zu den Zeitschritten der Analyse
Mit zunehmender Anzahl von Zeitschritten nimmt die Übereinstimmung zwischen den Ergebnissen unserer Finite-Elemente-Analyse und den theoretisch abgeleiteten Werten zu.
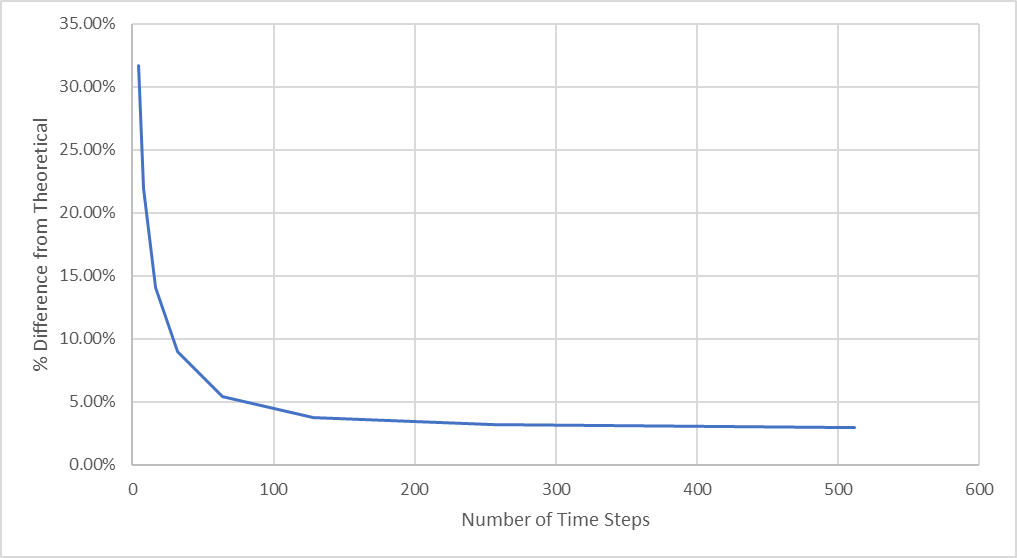
Abbildung 27: Prozentuale Abweichung von der theoretischen maximalen Durchbiegung
Aus dieser Abbildung geht hervor, dass sich die Konvergenz dramatisch verbessert, wenn die Anzahl der Zeitschritte zwischen 64 und 128 liegt, sich aber nur wenig ändert, wenn die Anzahl der Zeitschritte erhöht wird.
Aber was bedeutet das alles im Hinblick auf andere Ergebnisse, wie z.B. Stress?
Im Folgenden werde ich die maximale von-Mises-Spannung pro Zeit für verschiedene Analyseszenarien darstellen.
Abbildung 28: Von-Mises-Spannung bei der Lösung von 32 Zeitschritten
Abbildung 29: Von-Mises-Spannung bei der Lösung von 64 Zeitschritten
Abbildung 30: Von-Mises-Spannung bei der Lösung von 128 Zeitschritten
Abbildung 31: Von-Mises-Spannung bei der Lösung von 256 Zeitschritten
Abbildung 32: Von-Mises-Spannung bei der Lösung von 512 Zeitschritten
Zusammengefasst sehen wir das, wenn wir die Spannungen betrachten:
| Anzahl von Unterschritten | Max Durchschnittliche Spannung | Maximale Spitzenspannung | % Abweichung der durchschnittlichen Spannung |
| 4 | 120.04 | 301.98 | 29.62% |
| 8 | 136.4 | 316.61 | 20.03% |
| 16 | 150.57 | 312.42 | 11.72% |
| 32 | 159.15 | 301.68 | 6.69% |
| 64 | 165.4 | 283.51 | 3.03% |
| 128 | 168.84 | 303.99 | 1.01% |
| 256 | 170.05 | 354.35 | 0.30% |
| 512 | 170.56 | 442.08 | 0.00% |
Abbildung 33: Maximale Druckverschiebung des Stabes im Vergleich zu den Zeitschritten der Analyse
Wir sehen, dass die Spitzenwerte der Aufprallspannungen mit zunehmender Anzahl von Zeitschritten größer werden. Sie zeigen die größten Werte zu Beginn des Aufpralls und werden im Laufe des Ereignisses kleiner. Die durchschnittlichen Spannungen in der Stange steigen von Null auf einen Spitzenwert bei maximaler Kompression an und fallen dann nach dem Ende des Aufpralls wieder auf Null zurück. Wir können diese maximalen durchschnittlichen Spannungen unten aufzeichnen.
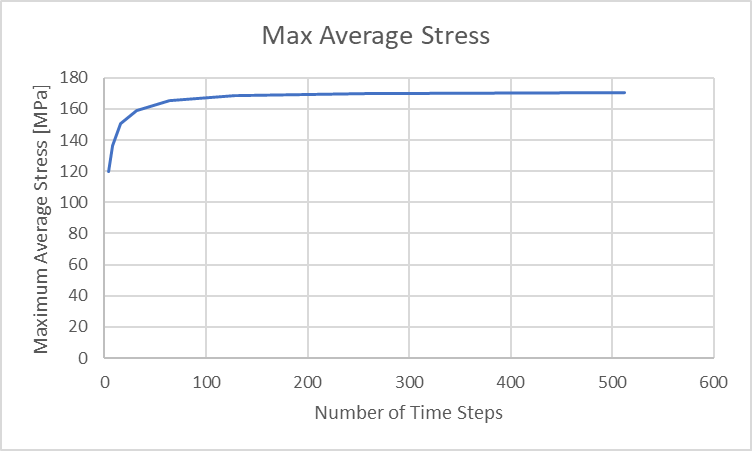
Abbildung 34: Maximale Druckverschiebung des Stabes im Vergleich zu den Zeitschritten der Analyse
Um diese maximalen Durchschnittsspannungen zu relativieren, können wir eine theoretische maximale Durchschnittsspannung in unserem Stab wie folgt berechnen:
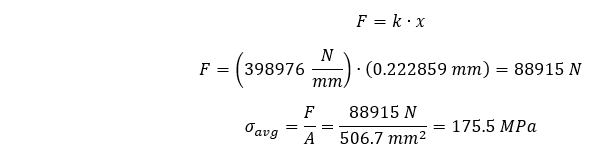
Wenn wir unsere maximalen Durchschnittsspannungen noch einmal mit den theoretisch berechneten maximalen Durchschnittsspannungen vergleichen, können wir den prozentualen Unterschied wie folgt zusammenfassen:
| Anzahl von Teilschritten | Max Durchschnittliche Spannung | Theoretische maximale durchschnittliche Spannung | % Abweichung |
| 4 | 120.04 | 175.5 | 31.60% |
| 8 | 136.4 | 175.5 | 22.28% |
| 16 | 150.57 | 175.5 | 14.21% |
| 32 | 159.15 | 175.5 | 9.32% |
| 64 | 165.4 | 175.5 | 5.75% |
| 128 | 168.84 | 175.5 | 3.79% |
| 256 | 170.05 | 175.5 | 3.11% |
| 512 | 170.56 | 175.5 | 2.81% |
Abbildung 35: Maximale Druckverschiebung des Stabes im Vergleich zu den Zeitschritten der Analyse
Wie bei den Durchbiegungen stellen wir auch hier eine signifikante Verbesserung der prozentualen Differenz zwischen unserer maximalen Durchschnittsspannung und der theoretisch berechneten maximalen Durchschnittsspannung fest, wenn wir zwischen 64 und 128 Zeitschritte für das Ereignis berücksichtigen. Die Verwendung von mehr Zeitschritten führt jedoch nur zu einer geringen Verbesserung der Genauigkeit unserer Ergebnisse.
Schlussfolgerung
Wir konnten nachweisen, dass die Energiemethoden, die zur Schätzung der maximalen Auslenkungen und der durchschnittlichen Spannungen für ein dynamisches Ereignis, wie z.B. den Fall eines elastischen Objekts auf eine harte Oberfläche, verwendet werden, vernünftige Ergebnisse liefern können und dass die signifikantesten Verbesserungen der Genauigkeit auftreten, wenn 64 bis 128 Zeitschritte für ein Ereignis berücksichtigt werden, dessen Periode der Eigenfrequenz unseres aufprallenden Objekts entspricht, die für die Aufprallrichtung berechnet wird. Wir haben auch festgestellt, dass die beste Methode zur Annäherung an diese Eigenfrequenz nicht durch manuelle Berechnungen, sondern durch eine modale Analyse mit Hilfe der Finite-Elemente-Methode erfolgt, insbesondere weil die Menge der beteiligten modalen effektiven Masse nicht leicht zu bestimmen ist.
Treten Sie dem Forum für Designer bei!
Ihr Fachwissen ist wichtig für die Gemeinschaft. Helfen Sie uns und bringen Sie Ihr Wissen ein!
Jetzt dem Forum beitretenTauschen Sie sich aus, lernen Sie und wachsen Sie mit den besten Fachleuten der Branche.

