Film-Walking

[Albest]

hallo, alle.
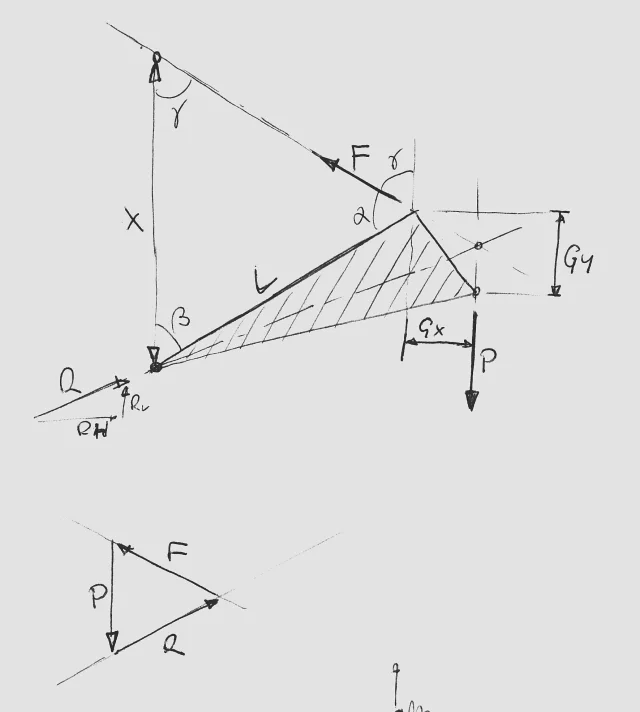
das filmische schema eines dreiecks mit variabler seite (draulic bleistift). ein rahmen ist mittels stiften eine stange und der stift verbunden, die ihn in unterschiedlichen höhen ein p-massenobjekt mit baricentro in g anheben können.
ich wollte wissen, wie man motorradgleichungen genau berechnet, indem man eine f-kraft des bleistifts aufsetzt. was ist der zustand von minimalem aufwand, um ein gutes heben und senken zu erhalten? ich möchte genau das system verschiedener kräfte und gleichungen....und möglicherweise das optimale x nach den anderen koordinaten fixiert g.
dank denen, die alles lösen konnten.:finger:

 

[Nicolas]

hi.
sie können einfach die gleichung der momente in den gleichgewichtsbedingungen (statisch oder dynamisch, dass es ist) mit dem pol auf dem festen stabscharnier anwenden, wonach sie die gleichung haben, die sie suchen.
andere straße (äquivalent) könnte sein, um plv anzuwenden und das gleiche ergebnis zu erhalten.
es gibt nur eine anfängliche geometrische betrachtung und dann kommt der rest von sich.

hi.

 

[SOLID]

ein rahmen ist mittels stiften eine stange und der stift verbunden, die ihn in unterschiedlichen höhen ein p-massenobjekt mit baricentro in g anheben können.

da der bleistift nur für die erste annäherung verwendet wird, können sie keine beschleunigungen berücksichtigen.

so kann die notwendige kraft gefunden werden, um dem bleistift die last zu unterstützen und die reaktion bindet an den fuß der auktion durch grafisch ausgleichende kräfte und momente.

zur bewertung der x-quote, für die sie die mindeststärke f haben, müssen sie mindestens zwei beta-konfigurationen berücksichtigen.
beta=90° spekulieren (niedrige position) und grafisch lösen sie haben, dass die kraft minimal zu machen, die x muss zu unendlich neigen, während für beta=0 (hohe position) die x, die minimiert f ist nur l.

natürlich ist die beta = 0 konfiguration aufgrund der martinet encumbrance nicht zu erreichen, so dass sie eine minimale beta berücksichtigen müssen, die dies berücksichtigt.