Ich habe mich mit gpt-4 auf Copilot beworben und die Antwort lautet wie folgt:
zur Berechnung des Drucks, der eine mit einem Aspo auf der Spindel gewickelte Metallbandspule erzeugt, können Sie die folgende Formel verwenden:
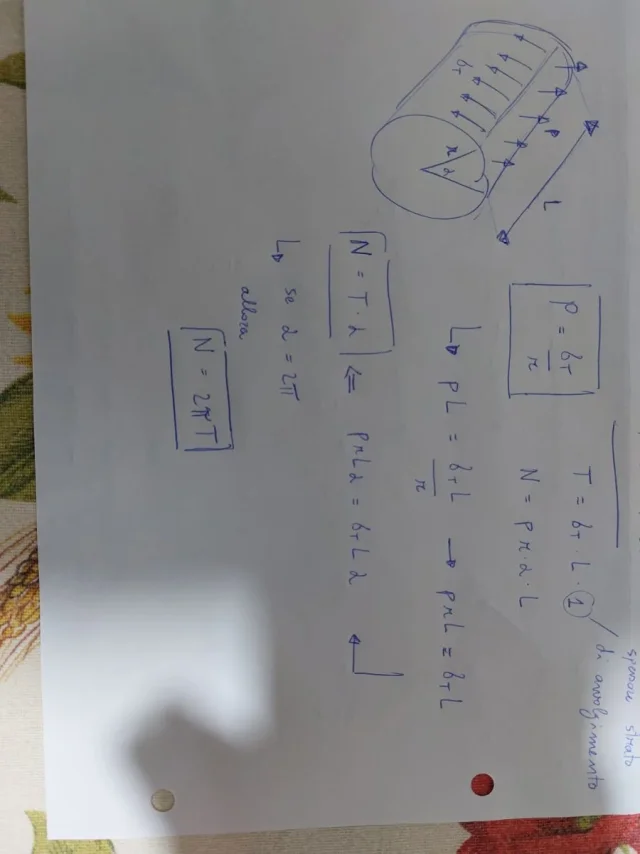
[math]p = \frac{f}{a}[/math]wenn [imath]p[/imath] è la press, [imath]f)[/imath] die vom Band auf die Spindel ausgeübte Kraft, [imath]eine[/imath] der Kontaktbereich zwischen Band und Spindel 1 ist.
Festigkeit [imath]f)[/imath] abhängig von der Spannung [imath]t[/imath] Band und Winkel [imath](alpha)[/imath] dass sich das Band mit der Spindel bildet. Sie können die folgende Formel verwenden:
[math]f = 2 t[/math]wenn [imath](alpha)[/imath] ist der Winkel zwischen den beiden Bandabschnitten, die aus der Rolle 2 herauskommen.
die Fläche [imath]eine[/imath] abhängig vom Radius [imath]R[/imath] Spindel und Breite [imath]w[/imath] Nastro. Wenn Sie die folgende Formel verwenden können:
[math]a = 2 \pi r w[/math]wenn [imath]R[/imath] ist der Spindelradius und [imath]w[/imath] die Breite des Bandes 3 ist.
die vorherigen Formeln in der Druckformel zu ersetzen, erhalten Sie:
[math]p = \frac{4 t \frac{\alpha}{2}{\pi\pi r w[/math]Diese Formel erlaubt es, den Druck, den das Band auf die Spindel ausübt, nach den Parametern des Bandes und der Spindel zu berechnen.Also fragte ich, ob es von der Anzahl der Wicklungen abhängt und die Antwort ist:
der Druck, der eine mit einem Aspo auf der Spindel gewickelte Spule aus Metallband erzeugt, wird nur indirekt durch die Anzahl der Wicklungen beeinflusst, da die Anzahl der Wicklungen die Bandlänge und damit die Spannung bestimmt, die sie auf der Spindel ausübt. wie Sie aus der Formel sehen können Ich habe in meiner vorherigen Antwort vorgeschlagen, dass der Druck von der Bandspannung, dem Spindelradius und der Bandbreite abhängt. wenn die Anzahl der Wicklungen zunimmt, erhöht sich die Länge des Bandes und dann nimmt die Spannung des Bandes ab, bei gleicher Kraft, die durch den Aspo aufgebracht wird. Dies führt zu einer Druckabnahme auf die Spindel. umgekehrt, wenn die Anzahl der Wicklungen abnimmt, nimmt die Länge des Bandes ab und damit erhöht sich die Spannung des Bandes bei gleicher Kraft, die durch die Aspo aufgebracht wird. Dies führt zu einer Druckerhöhung auf die Spindel. Daher wirkt sich die Anzahl der Wicklungen umgekehrt proportional auf den Druck aus, aber es ist nicht der einzige Faktor, der ihn bestimmt.und da es einen Bestandteil der Reibung gibt, wollte ich mich vertiefen:
die vorherige Formel nicht von Reibung, sondern nur von Bandspannung, Spindelradius und Bandbreite abhängt. diese Formel ist:
[math]p = \frac{4 t \frac{\alpha}{2}{\pi\pi r w[/math]wenn [imath]p[/imath] è la press, [imath]t[/imath] die Bandspannung, [imath](alpha)[/imath] der Winkel, den das Band mit der Spindel bildet, [imath]R[/imath] ist der Spindelradius und [imath]w[/imath] die Breite des Bandes 1 ist.
Diese Formel basiert auf der Hypothese, dass das Band ohne Überlappung gewickelt wird und dass die durch den Aspe aufgebrachte Kraft konstant ist. In Wirklichkeit kann die Reibung zwischen Band und Spindel die Spannung des Bandes und damit den Druck beeinflussen. wenn Reibung hoch ist, wird die Spannung des Bandes größer und damit auch Druck. wenn Reibung vernachlässigbar ist, wird die Spannung des Bandes geringer und damit auch Druck. Darüber hinaus kann Reibung eine Erwärmung von Band und Spindel verursachen, die die mechanischen Eigenschaften von Materialien verändern kann2.
um Reibung zu berücksichtigen, sollten Sie eine komplexere Formel verwenden, die den Reibungskoeffizienten zwischen Band und Spindel, die Anzahl der Wicklungen und die Variation der Spannung entlang des Bandes beinhaltet. diese Formel ist:
[math]p = \frac{4 t_0 \\frac{\alpha}{2} e\mu \theta}{\pi r w}[/math]wenn [imath]p[/imath] è la press, [imath]T_0[/imath] die anfängliche Spannung des Bandes, [imath](alpha)[/imath] der Winkel, den das Band mit der Spindel bildet, [imath]R[/imath] ist der Spindelradius, [imath]w[/imath] die Breite des Bandes, [imath]Insgesamt[/imath] der Reibungskoeffizient zwischen Band und Spindel ist, und [imath])[/imath] der Wickelwinkel des Bandes 3 ist.
Diese Formel zeigt, dass der Druck aufgrund der Reibungswirkung exponentiell mit der Windungszahl ansteigt. Um zu verhindern, dass der Druck zu hoch wird, sollte die Anzahl der Windungen begrenzt werden oder der Reibungskoeffizient reduziert werden.aber eigentlich versteht die Alpha-Ecke nicht, wie sie berechnet werden soll, also fragte ich.
die Ecke [imath](alpha)[/imath] dass sich das Metallband mit der Spindel bildet, hängt vom Spindelradius und der Anzahl der Bandwindungen ab. Je mehr Bandwindungen es gibt, desto mehr wird der Winkel reduziert. zur Berechnung des Winkels [imath](alpha)[/imath]Wenn ich die folgende Formel verwenden kann:
[math]<= <===================================================================[/math]wenn [imath]R[/imath] ist der Spindelradius, [imath]n[/imath] ist die Anzahl der Bandwindungen und [imath]w[/imath] die Breite des Bandes 4 ist.
Diese Formel basiert auf der Hypothese, dass das Band ohne Überlappung gewickelt wird und dass der Spindelradius konstant ist. tatsächlich erhöht sich der Spindelradius beim Hinzufügen von Bandwindungen, und dann der Winkel [imath](alpha)[/imath] variiert nicht linear. für eine genauere Formel sollten Sie den tatsächlichen Spindelradius an jedem Banddorn berücksichtigen, den Sie mit der folgenden Formel berechnen können:
[math]r_e = r + n w[/math]wenn [imath]R[/imath] Ist der tatsächliche Radius der Spindel, [imath]R[/imath] ist der Anfangsradius der Spindel, [imath]n[/imath] ist die Anzahl der Bandwindungen und [imath]w[/imath] die Breite des Bandes 3 ist.