Mello Dessi
Guest
Hallo, ich bin neu, und ich möchte für diejenigen danken, die mich beantworten werden.
Meine Frage ist:
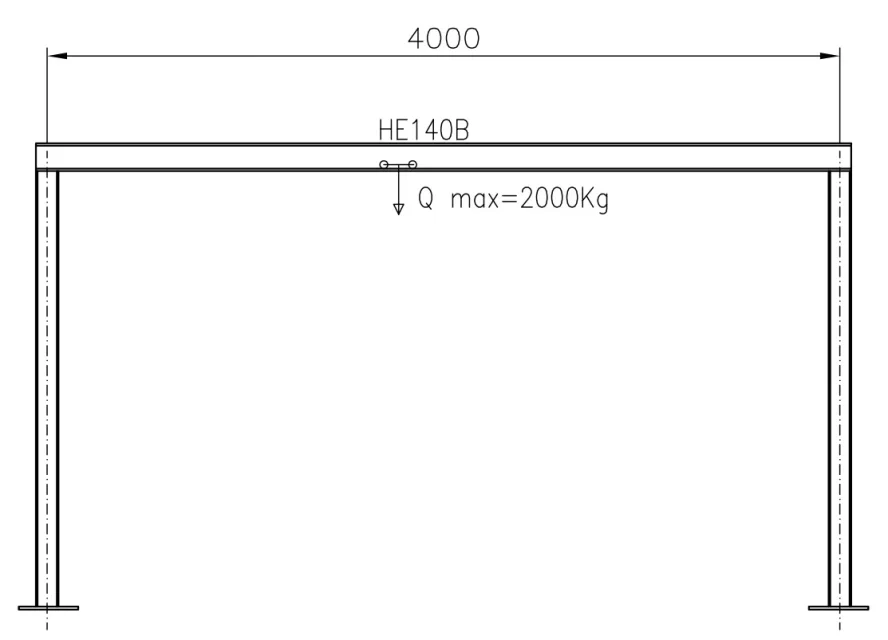
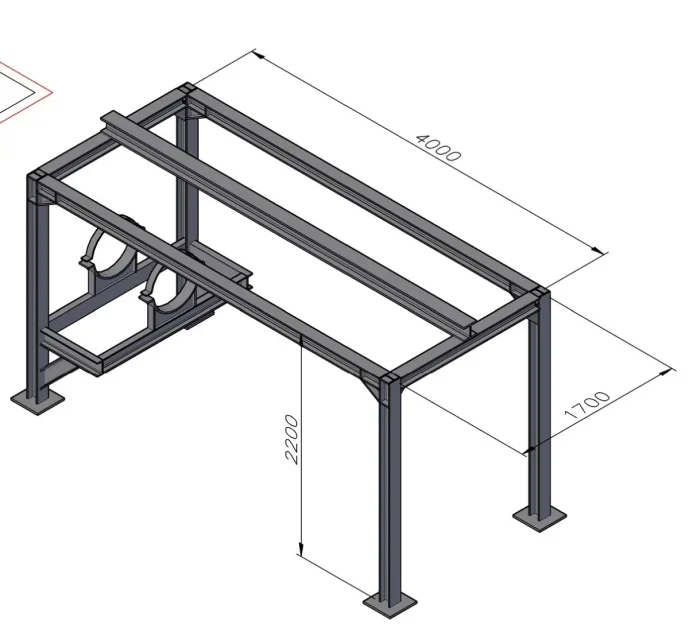
Ich sollte den Umfang eines heb140 Strahlmaterials s235 überprüfen, die 2 Träger sind im Abstand von 4mt, auf 2 Anlage verschweißt.
dieser Hub mit Rädern, es muss montiert werden und fließt auf dem unteren Flügel des Heb140.
der Hoist hat eine Kapazität von 2 Tonnen.
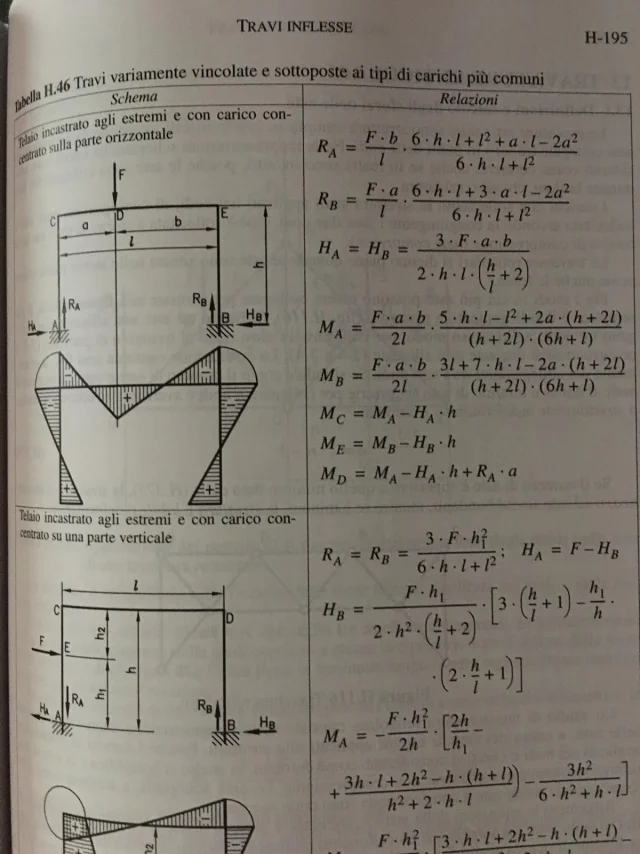
Ich wollte wissen, ob Sie allein die Größe des Flügels berechnen müssen (wie?) oder einfach den Strahl in der klassischen Weise berechnen, "mit konzentrierter Last doppelt stecken bleiben"? !
um das Foto besser zu verstehen:
Vielen Dank im Voraus
Grüße
Meine Frage ist:
Ich sollte den Umfang eines heb140 Strahlmaterials s235 überprüfen, die 2 Träger sind im Abstand von 4mt, auf 2 Anlage verschweißt.
dieser Hub mit Rädern, es muss montiert werden und fließt auf dem unteren Flügel des Heb140.
der Hoist hat eine Kapazität von 2 Tonnen.
Ich wollte wissen, ob Sie allein die Größe des Flügels berechnen müssen (wie?) oder einfach den Strahl in der klassischen Weise berechnen, "mit konzentrierter Last doppelt stecken bleiben"? !
um das Foto besser zu verstehen:
Vielen Dank im Voraus
Grüße