Davimont
Guest
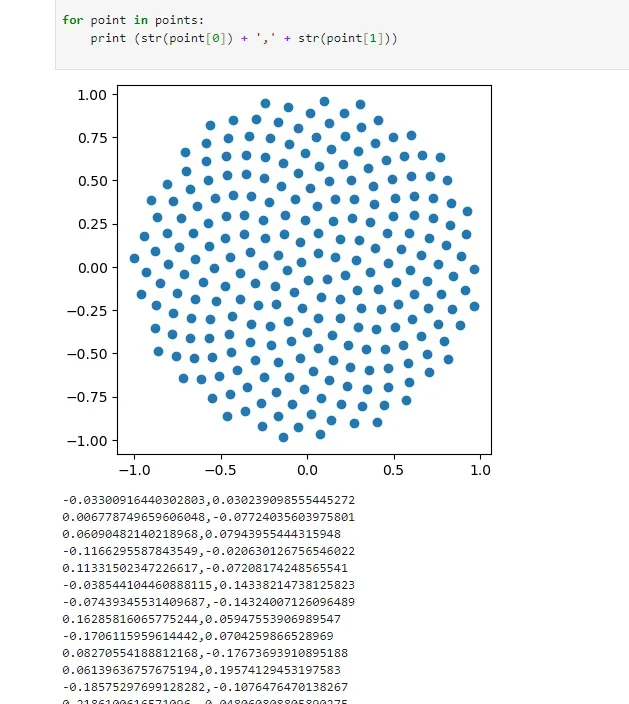
Jetzt und dann muss ich perforierte Kreisplättchen machen und ich weiß nie, wie man eine mehr oder weniger parametrische Serie schafft und dass es angenehm ist, die Sicht zu gestalten.
Ich lasse einen Platz, um das Material in der Ecke zu haben, um das erste Loch zu machen.
dann mache ich eine rechteckige Serie mit einer kleineren Kreisskizze als der Durchmesser der Platte, um die Serie nur innerhalb des Kreises zu begrenzen. Ich kümmere mich um den Abstand vom Rand, um keine Löcher zu haben, die vom Durchmesser ablaufen.
Wenn ich eine kreisförmige Serie wie die externe, die Sie im Bild sehen, dann weiß ich nicht, wie man sich innen bewegt, weil die Anzahl der Wiederholungen von Hand abnehmen sollte.
habt ihr irgendwelche Techniken?
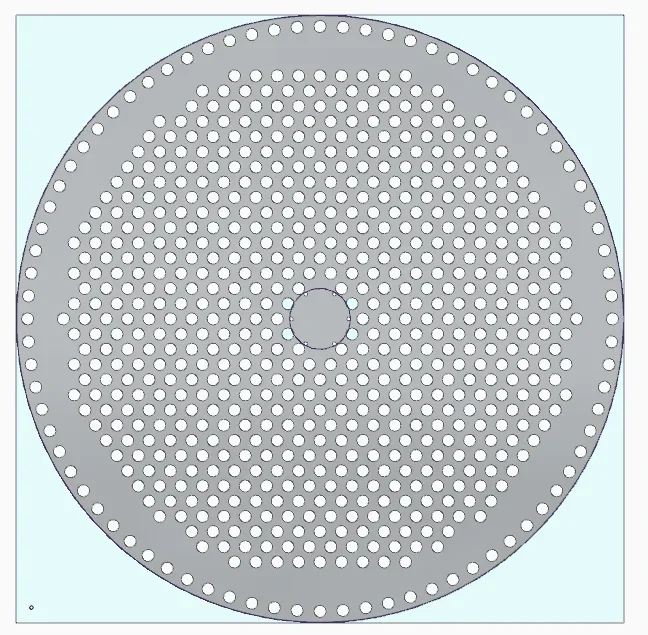
Ich lasse einen Platz, um das Material in der Ecke zu haben, um das erste Loch zu machen.
dann mache ich eine rechteckige Serie mit einer kleineren Kreisskizze als der Durchmesser der Platte, um die Serie nur innerhalb des Kreises zu begrenzen. Ich kümmere mich um den Abstand vom Rand, um keine Löcher zu haben, die vom Durchmesser ablaufen.
Wenn ich eine kreisförmige Serie wie die externe, die Sie im Bild sehen, dann weiß ich nicht, wie man sich innen bewegt, weil die Anzahl der Wiederholungen von Hand abnehmen sollte.
habt ihr irgendwelche Techniken?