Lernen aus dem Zwei-Kondensator-Paradoxon: Existieren Kapazität und Induktivität?

Treten Sie dem Forum für Designer bei!

Ihr Fachwissen ist wichtig für die Gemeinschaft. Helfen Sie uns und bringen Sie Ihr Wissen ein!

Tauschen Sie sich aus, lernen Sie und wachsen Sie mit den besten Fachleuten der Branche.

Das Zwei-Kondensator-Paradoxon ist ein provokantes Gedankenexperiment, das einige der Grenzen der Modellierung elektrischer Schaltkreise aufzeigen soll, und es gibt viele verschiedene Möglichkeiten, das Paradoxon zu lösen. Ich füge dem Mix eine Lösung hinzu, die in COMSOL Multiphysics modelliert werden kann.^® Software und erweitern Sie sie dann, um eine noch provokantere Frage zu stellen und zu beantworten: Existieren Kapazität und Induktivität? Tauchen wir ein!

Das Zwei-Kondensatoren-Paradoxon

Dieses Gedankenexperiment wird in der Regel wie folgt dargestellt: Betrachten Sie ein Gerät, das aus zwei gleichwertigen Kondensatoren besteht, mit einer Kapazität, C, parallel geschaltet mit einem offenen Schalter dazwischen. Alle Drähte und Kondensatoren bestehen aus idealen, perfekt widerstandsfreien, verlustfreien Materialien. Einer der Kondensatoren wird auf ein Potenzial aufgeladen, V_iDie gespeicherte Ladung ist also Q = CV_i. Auf dem anderen Kondensator gibt es keine Potentialdifferenz, er hat also keine gespeicherte Ladung. Was passiert, wenn Sie den Schalter schließen?

Schematische Darstellung des Zwei-Kondensator-Paradoxons. Ein Kondensator hat eine Potentialdifferenz zwischen den Platten. Was passiert, wenn der Schalter geschlossen ist?

Bei einigen Darstellungen dieses Gedankenexperiments wird ein Ablenkungsmanöver eingefügt und behauptet, dass die Ladung des ersten Kondensators in den zweiten Kondensator fließt, wodurch die Potenzialdifferenz des ersten Kondensators verringert und die des zweiten erhöht wird, bis ein stabiler Zustand erreicht ist – an diesem Punkt ist die Potenzialdifferenz auf beiden Kondensatoren gleich und die Hälfte der V_i, da die gleiche Ladung, Qwird nun auf zwei gleichwertige Kondensatoren verteilt. Dies führt jedoch sofort zu einem Paradoxon, denn die Energie in jedem Kondensator ist W_C = \frac{1}{2} C \Delta V^2. Wenn die Anfangsenergie \frac{1}{2} C V_i^2 und die Endenergie ist 2 \frac{1}{2} C\left( V_i/2 \right)^2 = \frac{1}{4} C V_i^2Wo ist die andere Hälfte der Energie geblieben?

Es gibt viele Lösungen, die sich auf alles von der Quantenmechanik bis zur Thermodynamik berufen. Vom pädagogischen Standpunkt aus sind diese Lösungen wahrscheinlich alle gültig. Viele von ihnen appellieren jedoch implizit an die Realität, indem sie sagen, dass die Drähte und Kondensatoren einfach einen gewissen Widerstand oder eine gewisse Induktivität haben müssen. Aber warum? Zumindest im Rahmen eines Gedankenexperiments mag es vernünftig sein, von vollkommen verlustfreien Materialien auszugehen und den Widerstand zu vernachlässigen. Aber was ist mit der Induktivität? Können wir im Rahmen dieses Gedankenexperiments die Induktivität vernachlässigen? Lassen Sie uns dieser Frage nachgehen und sehen, ob sie eine interessante Antwort liefert…

Eine einfache Lösung für das Paradoxon

Unser Gerät besteht aus zwei idealen, verlustfreien Kondensatoren. Aber selbst ein idealer Kondensator muss seine Ladungen räumlich trennen. Das heißt, ein Kondensator muss eine gewisse Größe haben. Und wenn jeder Kondensator eine Größe hat, dann muss er durch einen Abstand ungleich Null von dem anderen Kondensator getrennt sein. Wenn wir also unser Diagramm ein wenig umzeichnen, sehen wir, dass wir zwei Kondensatoren und zwei Halbschleifen aus verlustfreiem Draht mit endlichem Durchmesser haben, durch die ein zeitlich variabler Strom fließen kann. Aber wie nennen wir eine solche Struktur? Eine Induktionsspule!

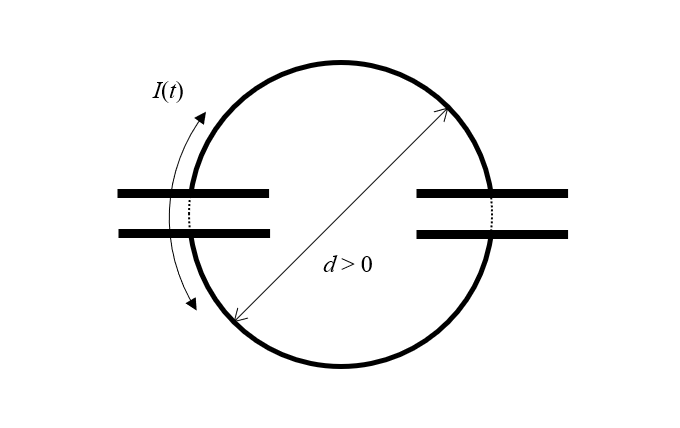
Das Paradoxon lässt sich auflösen, wenn man sich klarmacht, dass die Struktur eine Größe ungleich Null haben muss, wobei der Strom um eine Schleife mit endlicher Fläche fließt, und daher auch ein Induktor ist.

Die Struktur, die wir hier gezeichnet haben, muss eine endliche Größe haben und damit auch eine Induktivität, solange sie in unserem Universum existiert, wo der freie Raum eine magnetische Permeabilität hat. Es ist also nur eine Folge des Kondensators in unserem Schaltkreis, dass es auch eine Induktivität in dem Schaltkreis geben muss. Es wird sogar noch besser: Wenn wir eine Drosselspule haben, sogar eine verlustfreie, führt jeder zeitlich veränderliche Strom, der durch sie fließt, zu einem elektrischen Feld, das zwischen den Windungen der Drosselspule existiert. Daher wirkt jede Drosselspule, die wir zu dieser Schaltung hinzufügen, auch als Kondensator! Wir könnten diese Logik endlos weiterverfolgen, aber für unsere Zwecke reicht es aus, unsere Schaltung mit einer einzigen Induktivität zu modifizieren, die eine Induktivität hat, L.

Wir haben jetzt eine LC Schaltung, und dafür gibt es eine analytische Lösung, die das Paradoxon sofort aufklärt: Der Strom fließt zwischen den Kondensatoren und entlang der endlich langen Drähte hin und her und schwingt mit einer Frequenz, die durch gegeben ist: f=1/\sqrt{2\pi LC}. Es wird nie eine stationäre Lösung geben, daher können wir niemals nur die elektrostatische Energie bewerten. Wir müssen auch die Energie berücksichtigen, die durch die sich bewegenden Ladungen, d.h. den Stromfluss, entsteht, Iund diese ist gegeben durch: W_L = \frac{1}{2} L I^2. Die Summe aus dieser elektrischen und magnetischen Energie (\frac{1}{2} L I^2 + \frac{1}{2} C V^2) wird sich im Laufe der Zeit nicht ändern.

Überprüfen in COMSOL Multiphysics^® Software

Es ist einfach, ein Modell zu erstellen, das diese Situation mit COMSOL Multiphysics verifiziert^® und das RF-Modul. Wir verwenden dazu die Elektromagnetische Wellen, transiente Schnittstelle zusammen mit dem Elektrostatik Schnittstelle, um die Anfangsbedingungen zu berechnen. Wir werden eine kleine Region mit perfektem Vakuum modellieren, in der sich die Kondensatoren und Drähte befinden. Die Kondensatorplatten, die Drähte und der Raum um unser Volumen herum werden alle als perfekte elektrische Leiter behandelt, was bedeutet, dass die elektromagnetischen Felder keine Grenzen durchdringen werden. In unserem Learning Center-Artikel finden Sie eine Anleitung zum Aufbau solcher Modelle mit kapazitiver Entladung: „Modellierung der kapazitiven Entladung“.

Die Lösung dieses Zeitbereichsmodells und die Auswertung der gesamten elektrischen und magnetischen Energie zeigt das erwartete oszillierende Verhalten. Es ist auch möglich, den Modellierungsbereich in verschiedene Regionen aufzuteilen, um die Gesamtenergie in den Regionen um die beiden Kondensatoren sowie im umgebenden Raum zu bewerten. Diese Grafik zeigt, wie die Energie sowohl im Raum als auch in der Zeit oszilliert.

Die Animation zeigt die Ströme auf der Oberfläche der Kondensatorplatten und -drähte sowie das Magnetfeld im Zwischenraum.

Die elektrische und magnetische Gesamtenergie schwankt im Laufe der Zeit; die Summe ändert sich in diesem verlustfreien Gerät nicht.

Die Summe der elektrischen und magnetischen Energie in verschiedenen Bereichen zeigt, dass die Energie in Zeit und Raum schwankt.

Wir können feststellen, dass diese Darstellungen nicht rein sinusförmig in der Zeit sind, und wir sollten uns fragen, warum das so ist. Woher kommt dieser höherfrequente Inhalt, d.h. die Wellen der Energie im Laufe der Zeit? Sie entstehen durch die Struktur. Es ist ganz klar, dass die beiden Platten eine klar definierte Kapazität haben, aber es gibt auch eine Ladungstrennung durch die Drähte, und diese ganze Struktur befindet sich in einem zylindrischen Hohlraum, der eine Resonanzfrequenz hat. Alle diese verschiedenen Teile des Geräts tragen in gewisser Weise zum elektromagnetischen Verhalten bei. Jeder einzelne Beitrag kann recht klein sein, aber er ist immer vorhanden, wenn wir eine Struktur von endlicher Größe betrachten.

Mehr Fragen stellen: Existieren Kapazität und Induktivität?

Es ist nun an der Zeit, eine provokantere Frage zu diesem (oder jedem anderen) elektromagnetischen Gerät zu stellen: Besitzt es eine Kapazität oder eine Induktivität? Wir haben deutlich gesehen, dass dieses spezielle Gerät beides hat. Aber was wäre, wenn wir es modifizieren würden, indem wir ein sehr starkes dielektrisches Material zwischen den Kondensatorplatten hinzufügen? Das würde die Kapazität viel größer machen, aber die Induktivität unverändert lassen. Und wenn wir die Kapazität viel größer machen würden, könnten wir dann sagen, dass die Induktivität keine Rolle spielt?

Kurz gesagt: Nein, wir sollten ein elektrodynamisches Gerät niemals als rein kapazitiv oder rein induktiv betrachten. In einem elektrodynamischen Gerät gibt es immer elektrische Energie aufgrund der räumlichen Trennung von Ladungen und magnetische Energie aufgrund der Bewegung von Ladungen. Obwohl wir manchmal hypothetische Situationen konstruieren können, in denen das eine oder das andere ignoriert werden kann, müssen wir immer daran denken, dass wir eine mentale Vereinfachung vornehmen.

Darüber hinaus haben alle realen Materialien auch einen gewissen endlichen Widerstand. Um realistischer zu sein, sollten wir also davon sprechen, dass alles eine Impedanz hat – und genau das ist der Punkt, an dem wir uns manchmal in noch größere Schwierigkeiten bringen. Wenn wir mit einem Modell im Frequenzbereich arbeiten, gibt es einen sehr bekannten Ausdruck für die Impedanz eines elektrischen Geräts:

Z = R + j\omega L -j\frac{1}{\omega C}

Der Widerstand, Rin diesem Ausdruck ist ein Maß dafür, wie die kinetische Energie der sich bewegenden Ladungen, d.h. der Strom, in Wärmeenergie umgewandelt wird.

Man erkennt sofort, dass sich diese Gleichung auf einen gedämpften harmonischen Oszillator mit einem Freiheitsgrad bezieht, der eines der am besten untersuchten Probleme in Technik und Physik ist. Wir wissen, dass wir aus diesem Ausdruck die Resonanzfrequenz und den Gütefaktor eines solchen Oszillators berechnen können, und wir wissen, dass reale Geräte eine Grundresonanz und einen Gütefaktor haben. Das verleitet uns dazu, die beiden gleichzusetzen und zu versuchen, ein reales elektrisches Gerät in endlicher Größe auf einen einzigen Widerstand, eine Kapazität und eine Induktivität zu reduzieren. Das ist ein konzeptioneller Fehler und ist niemals gültig, denn der obige Ausdruck für die Impedanz gilt nur für ein Gerät, das eine infinitesimale Größe hat.

Jedes reale Gerät hat eine endliche Größe, und wenn es in Resonanz arbeitet, variieren die elektrische und magnetische Energie in Raum und Zeit, wie wir in den obigen Diagrammen gesehen haben. Daher benötigt ein Ersatzschaltbildmodell mindestens drei Knoten, manchmal aber auch viel mehr. Wenn wir an unser physikalisches Modell der beiden Kondensatoren zurückdenken und davon ausgehen, dass die Platte jedes Kondensators durch einen Knoten in der elektrischen Schaltung dargestellt wird, sehen wir, dass das Ersatzschaltbild mindestens so kompliziert sein müsste wie die unten abgebildete Schaltung mit vier Knoten. Beachten Sie, dass parallel zur Induktivität der Drähte eine kleine Kapazität hinzugefügt wurde, da es auch entlang der Drähte eine Ladungstrennung gibt.

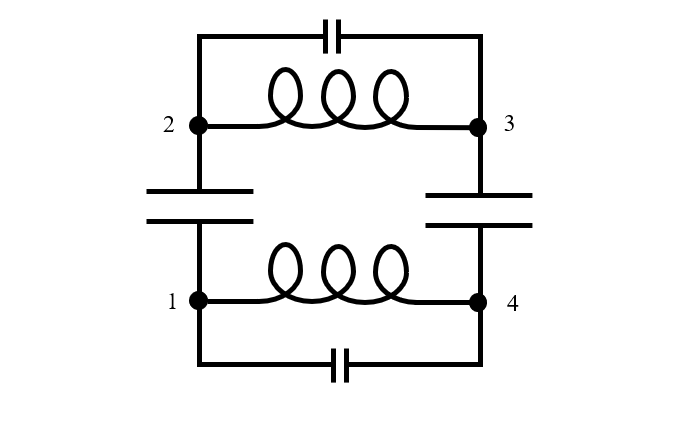
Ein Ersatzschaltbild für zwei in Reihe geschaltete verlustfreie Kondensatoren endlicher Größe.

Anhand dieses Beispiels können wir hoffentlich erkennen, dass die Konstruktion eines Ersatzschaltbildes, das in der Nähe der Resonanz gültig ist, schnell sehr kompliziert werden kann und physikalisches Verständnis, eine gute Portion Erfahrung mit ähnlichen Geräten und numerische Modellierung erfordert.

Um auf die ursprüngliche Frage zurückzukommen, könnte man argumentieren, dass Kapazität, Induktivität und sogar Widerstand Konzepte sind, die für sich allein nicht existieren – dass sie nur in Kombination miteinander existieren. Obwohl wir die frequenzabhängige Impedanz eines Geräts manchmal auf einen einzelnen Widerstand, eine Kapazität und/oder eine Induktivität reduzieren können, sind solche Vereinfachungen nur bei Frequenzen unterhalb der Resonanz des Geräts gültig. Wenn wir dies im Hinterkopf behalten, können wir alle möglichen Fallstricke vermeiden, von diesem unterhaltsamen Zwei-Kondensator-Paradoxon bis hin zu viel frustrierenderen und komplexeren Problemen in der realen Welt.

Schlussbemerkungen

Wir haben hier ein klassisches Gedankenexperiment verwendet, um zu verstehen, warum die Impedanz eines elektromagnetischen Geräts, das nahe der Resonanz arbeitet, nicht in einen einzigen äquivalenten Widerstand, eine Kapazität und eine Induktivität zerlegt werden kann. Gedankenexperimente wie das Zwei-Kondensator-Paradoxon sind wertvoll, um unser Verständnis der Elektromagnetik zu erweitern und die Ergebnisse unserer Berechnungsmodelle zu interpretieren.

Weitere Lektüre

Möchten Sie erfahren, wie Modellierung und Simulation zur Lösung anderer Rätsel eingesetzt werden können? Sehen Sie sich einige andere Beispiele im COMSOL Blog an:

Treten Sie dem Forum für Designer bei!

Ihr Fachwissen ist wichtig für die Gemeinschaft. Helfen Sie uns und bringen Sie Ihr Wissen ein!

Tauschen Sie sich aus, lernen Sie und wachsen Sie mit den besten Fachleuten der Branche.