Treten Sie dem Forum für Designer bei!
Ihr Fachwissen ist wichtig für die Gemeinschaft. Helfen Sie uns und bringen Sie Ihr Wissen ein!
Jetzt dem Forum beitretenTauschen Sie sich aus, lernen Sie und wachsen Sie mit den besten Fachleuten der Branche.
Methoden zur Reduzierung der Modellordnung beziehen sich auf eine Technik zur Anwendung von Ersatzmodellen, auch bekannt als Transferfunktionen oder Approximationsmodelle, um Produktdesignalternativen effizient zu untersuchen. Näherungsmodelle sind hocheffektive, schnell ablaufende mathematische Modelle, die anstelle von Simulationsmodellen mit höherer Genauigkeit und langer Laufzeit verwendet werden, wie sie für die Finite-Elemente-Analyse (FEA), die numerische Strömungsmechanik (CFD) und die elektromagnetische Analyse (EMAG) typisch sind. Alle Simulationswerkzeuge sind Annäherungen an die Realität. Die Realität beinhaltet physische Tests unter den Bedingungen, unter denen ein Produkt verwendet wird. Die Kosten und der Zeitaufwand für physische Tests sind jedoch in der Regel zu hoch. Stattdessen verwenden Simulationsexperten High-Fidelity-Simulationstools, um physische Tests zu ersetzen oder zu reduzieren.
Selbst bei der heute zur Verfügung stehenden Rechenleistung können die Rechenzeit und die Kosten für diese High-Fidelity-Simulationen unerschwinglich sein, insbesondere bei der Durchführung von Design of Experiments (DOE), Optimierung oder stochastischen Methoden. Stattdessen können Methoden zur Reduzierung der Modellordnung verwendet werden, um die Rechenzeit und die Kosten zu minimieren. Diese Methoden erfordern immer noch einen gültigen Stichproben-Datensatz, um das mathematische Modell zu entwickeln. Eine kleine Stichprobe aus dem Designraum unter Verwendung des High-Fidelity-Simulationstools, das durch eine Design of Experiments-Methode gesteuert wird, kann ausreichen, um ein zuverlässiges und genaues Näherungsmodell zu erstellen.
Dassault Systèmes‘ SIMULIA Isight Lösung
Isight bietet Designern, Ingenieuren und Forschern ein offenes System zur Integration von Design- und Simulationsmodellen, die mit verschiedenen CAD-, CAE- und anderen Softwareanwendungen erstellt wurden, um die Ausführung von Simulationen zur Designuntersuchung und -optimierung zu automatisieren. Die Softwarelösung kann auf einfache Weise ein Näherungsmodell für eine beliebige Aufgabe oder eine einzelne Anwendungskomponente aus einer beliebigen Quelle von Simulations- oder Testergebnisdaten erstellen. Die Verwendung von Isight zur Erstellung von Näherungsmodellen bietet zahlreiche Vorteile:
- Liefern Sie zuverlässigere und robustere Produkte durch eine beschleunigte Bewertung von Designalternativen
- Reduzieren Sie die Design-Zykluszeit durch integrierte Arbeitsabläufe
- Integrieren Sie Modelle, die in gängiger kommerzieller Software entwickelt wurden, und selbst entwickelte Codes
- Manipulieren Sie parametrische Daten und ordnen Sie sie zwischen Prozessschritten und mehreren Simulationen zu, um die Effizienz mit weniger manuellen Fehlern zu verbessern.
- Überprüfen Sie die Genauigkeit des Modells und fügen Sie automatisch zusätzliche Datenpunkte hinzu, um die gewünschte Genauigkeit zu erreichen.
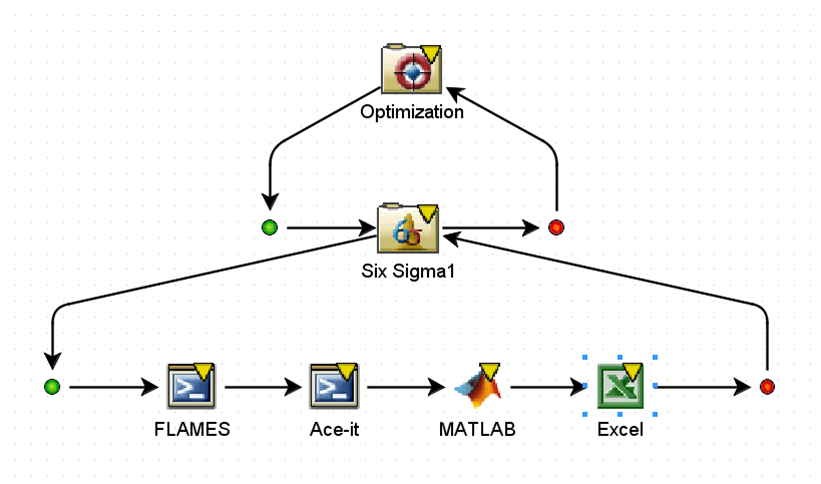
In Isight verfügbare Näherungsmodelle
Es gibt verschiedene Arten von Approximationsmodellen. Es gibt keine einzige Technik, die für alle Anwendungen am besten geeignet ist, da die physikalischen Gegebenheiten unterschiedlich sind. Die verschiedenen Arten von Approximationsmodellen, die in Isight verfügbar sind, werden im Folgenden beschrieben:
Reaktionsoberflächenmodelle (RSM)
RSMs sind Polynome bis zur 4. Ordnung mit vier Term Selection Techniken. Sie können Term Selection verwenden, um einige Polynomterme mit geringer Bedeutung zu entfernen. Dies kann die Zuverlässigkeit der Approximation verbessern und die Anzahl der erforderlichen Entwurfspunkte reduzieren.
- Sequentielle Ersetzung
- Schrittweiser Efroymson
- Zwei auf einmal ersetzen
- Ausführliche Suche
Kriging
Die Kriging-Approximation ist eine Art von Interpolationstechnik. Kriging-Approximationen sind aufgrund der großen Auswahl an Korrelationsfunktionen, die für den Aufbau des Metamodells gewählt werden können, äußerst flexibel. Darüber hinaus kann das Metamodell je nach Wahl der Korrelationsfunktion entweder „die Daten ehren“, was eine exakte Interpolation der Daten bedeutet, oder „die Daten glätten“, was eine ungenaue Interpolation bedeutet.
Die Isight-Implementierung von Kriging-Modellen ermöglicht die Verwendung der gängigen Korrelationsfunktionen wie Exponential, Gauß, Matern Linear und Matern Cubic.
Die Initialisierung der Kriging-Approximation erfordert mindestens 2n+1 Designpunkte, wobei n ist die Anzahl der Eingaben. Die zu approximierende Komponente kann mehrfach ausgeführt werden, um die erforderlichen Daten zu sammeln. Alternativ kann auch eine Datendatei als Initialisierungsquelle dienen.
Orthogonales Polynom
Die orthogonale Polynomapproximation ist eine Art von Regressionstechnik. Orthogonale Polynome minimieren die Autokorrelation zwischen den Antwortwerten, die aufgrund des Stichprobenortes besteht. Ein weiterer Vorteil der Verwendung von Funktionen, die in Bezug auf die Daten orthogonal sind, ist, dass die Eingaben in der Varianzanalyse (ANOVA) entkoppelt werden können.
Orthogonale Tschebyscheff-Polynome sind eine gängige Art von orthogonalen Polynomen, die besonders nützlich für gleichmäßig verteilte Stichprobenpunkte sind. Sie werden verwendet, wenn die Abtaststrategie ein orthogonales Array ist. Isight erlaubt die Verwendung von Tschebyscheff-Polynomen auch dann, wenn andere Stichprobenstrategien verwendet werden. In diesem Fall kann die ANOVA jedoch nicht berechnet werden.
Isight bietet auch die Möglichkeit, orthogonale Polynomnäherungen für andere Arten von Stichproben zu erzeugen. Die Technik der sukzessiven orthogonalen Polynome erzeugt eine Reihe von Polynomen, die in Bezug auf die bereitgestellten Daten orthogonal sind. Diese Polynome werden dann als Basisfunktionen verwendet, um eine Approximation für die Antworten zu erhalten. Beachten Sie, dass die Basisfunktionen nur von den Probenorten und nicht von den Antwortwerten abhängen.
Die Initialisierung der orthogonalen Polynomnäherung erfordert mindestens 2d+1 Designpunkte, wobei d ist der Grad des erwarteten Polynoms. Die Datendatei muss die erforderliche Anzahl von Datenpunkten enthalten.
Radiale Basisfunktion
Die Radial Basis Function (RBF)-Approximation ist eine Art neuronales Netzwerk, das eine versteckte Schicht mit radialen Einheiten und eine Ausgabeschicht mit linearen Einheiten verwendet. RBF-Approximationen zeichnen sich durch ein relativ schnelles Training und relativ kompakte Netzwerke aus. Sie eignen sich für die Approximation einer Vielzahl von nichtlinearen Räumen.
Elliptische Basisfunktionen (EBFs) ähneln der Radialen Basisfunktion, verwenden aber elliptische Einheiten anstelle von radialen Einheiten. Im Vergleich zur RBF, bei der alle Eingaben gleich behandelt werden, behandeln EBF-Netzwerke jede Eingabe separat mit individuellen Gewichten.
RBF-Netzwerke zeichnen sich durch ein relativ schnelles Training und relativ kompakte Netzwerke aus. EBF-Netzwerke hingegen benötigen mehr Iterationen, um die einzelnen Eingangsgewichte zu lernen und sind oft genauer als RBFs.
Die Initialisierung der RBF-Approximation erfordert mindestens 2n+1 zu bewertende Designpunkte, wobei n ist die Anzahl der Eingaben. Die zu approximierende Komponente kann mehrfach ausgeführt werden, um die erforderlichen Daten zu sammeln. Alternativ kann auch eine Datendatei als Initialisierungsquelle dienen.
Automatische Generierung und Kreuzvalidierung von Approximationsmodellen
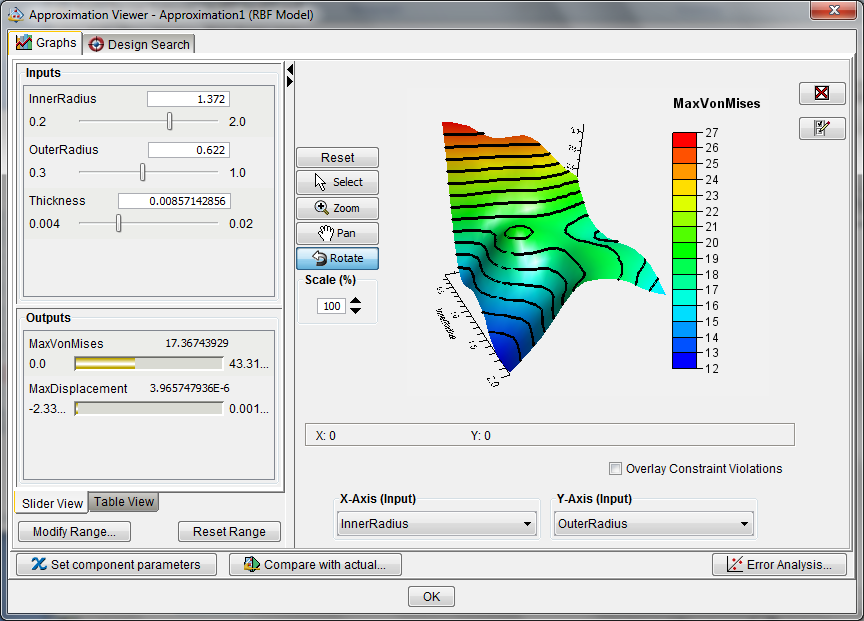
Alle Methoden zur Reduzierung der Modellordnung in Isight unterstützen die automatische Generierung und Kreuzvalidierung von Approximationsmodellen mit leicht verständlicher visueller Fehleranalyse. Die Oberfläche zur Erstellung von Approximationsmodellen in Isight ermöglicht es dem Benutzer, Approximationsoberflächen in 2D und 3D zu visualisieren – siehe Abbildung 2 unten.
In Abbildung 3 sehen Sie einen typischen Isight-Workflow, der ein Näherungsmodell enthält. Wie bereits erwähnt, kann ein Näherungsmodell auf einem ganzen Prozess, einem Teilprozess oder einer einzelnen Komponente abgelegt werden oder als eigenständige Komponente in den Workflow eingefügt werden, wenn das Modell zuvor gespeichert wurde oder Daten zur Erstellung des Modells vorhanden sind. Wenn das Näherungsmodell auf einem Prozess, einem Teilprozess oder einer einzelnen Komponente abgelegt wird und keine Daten für die Initialisierung vorhanden sind, führt Isight den Prozess automatisch aus, bis es die Mindestanzahl von Punkten für die anfängliche Erstellung der Näherung erhält.
Anschließend führt Isight automatisch eine Fehleranalyse durch, indem es einen Entwurfspunkt mit dem Näherungsmodell ausführt und dann die Simulation, für die die Näherung gilt, durchführt. Wenn die Ergebnisse zwischen dem approximierten und dem tatsächlichen Lauf um einen bestimmten Prozentsatz voneinander abweichen, fügt Isight weitere Läufe der tatsächlichen Simulation zum Approximationsmodell hinzu, bis die Fehlertoleranz erfüllt ist.
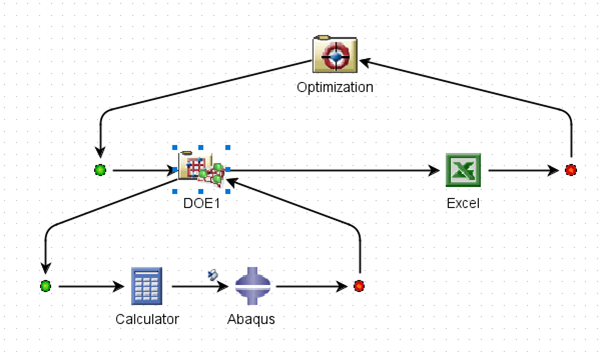
Diese automatische Generierung/Initialisierung eines Näherungsmodells kann Teil einer beliebigen Design Explorationstechnik sein: DOE, Optimierung, Monte Carlo, Six Sigma, usw. Der endgültige „beste“ Entwurf aus der Annäherung kann dann automatisch mit dem eigentlichen Simulationstool erneut ausgeführt werden, so dass Sie die vollständigen Simulationsergebnisse des von Ihnen gewählten Tools erhalten.
Treten Sie dem Forum für Designer bei!
Ihr Fachwissen ist wichtig für die Gemeinschaft. Helfen Sie uns und bringen Sie Ihr Wissen ein!
Jetzt dem Forum beitretenTauschen Sie sich aus, lernen Sie und wachsen Sie mit den besten Fachleuten der Branche.

