Treten Sie dem Forum für Designer bei!
Ihr Fachwissen ist wichtig für die Gemeinschaft. Helfen Sie uns und bringen Sie Ihr Wissen ein!
Jetzt dem Forum beitretenTauschen Sie sich aus, lernen Sie und wachsen Sie mit den besten Fachleuten der Branche.
Die Techniken, die als Treiber für Adapter in Process Composer verfügbar sind, sind großartig. Sie sind das Ergebnis eingehender Forschung im Bereich numerischer Methoden. Die bekanntesten Techniken sind DOE, Optimierung, Approximationen und Six-Sigma. Wir haben DOE in früheren Blogs ausführlich besprochen. In diesem Blog tauchen wir tief in die Optimierung ein. Vergessen wir nicht, dass wir uns im Process Composer befinden, die Optimierung ist also parametrisch und wird hauptsächlich durch geometrische oder physikalische Parameter gesteuert.
Die klassische Optimierungsdefinition
Irgendwo auf dem eingezäunten Feld haben Sie einen Ball. Sie haben einen Ausgangspunkt. Sie müssen den Ball finden, indem Sie die Mindeststrecke zurücklegen, ohne den Zaun zu überqueren. Sie verfügen über Sensoren zur Unterstützung. Der Ball ist die Zielfunktion. Die Zäune sind Einschränkungen. Als Optimierungstechniken kommen die Sensoren zum Einsatz.

Der Unterschied zwischen Versuchsplanung und Optimierung
Der Unterschied zwischen den beiden ist derselbe wie der Unterschied zwischen „besser“ und „am besten“. Bei der Versuchsplanung handelt es sich um eine Methode zur effizienten Auswahl des am besten geeigneten Entwurfspunkts aus einem Pool bestehender Punkte. Dieser Satz kann entweder vom Benutzer oder vom DOE selbst definiert werden. Die Optimierungstechniken beginnen mit einem einzelnen anfänglichen Entwurfspunkt und navigieren iterativ durch den Entwurfsraum, um zum optimalen oder besten Entwurfspunkt zu gelangen. Abhängig vom Problem kann das DOE ein Vorläufer der Optimierung sein.
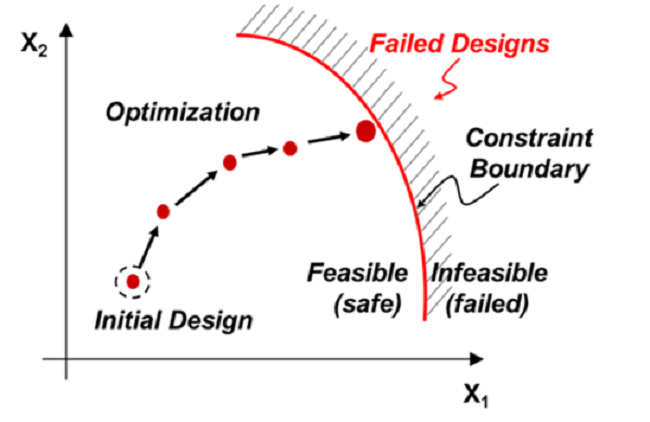
Arten von Optimierungstechniken
Abhängig von der Definition der Zielfunktion und der Art des geeigneten Gestaltungsraums gibt es unterschiedliche Methoden zur Kategorisierung.
Eingeschränkte Techniken: Für ihre Arbeit verwenden sie separate Funktionen, eine für das Ziel und eine für die Einschränkungen. Wir alle haben solche Techniken schon einmal in Ingenieurstudiengängen kennengelernt. Sie sind die häufigsten.
Minimieren/Maximieren Sie F(x) in x1>x>x2
Vorbehaltlich: h(x)>a1; g(x)>a2; f(x)=0 usw.
Uneingeschränkte Techniken: Sie verwenden nur eine Funktion sowohl für das Ziel als auch für die Einschränkungen. Der Benutzer hat weiterhin vom Ziel getrennte Einschränkungen definiert, aber intern wird das eingeschränkte Problem in ein uneingeschränktes Problem umgewandelt.
Basierend auf der Anwendung auf verschiedene Arten von Designräumen können Optimierungsmethoden in die Kategorien „Gradientenbasiert“, „Direkt“ und „Exploratorisch“ eingeteilt werden. Die in den Bildern unten gezeigten Abkürzungen sind die Namen der Methoden in den jeweiligen Kategorien.
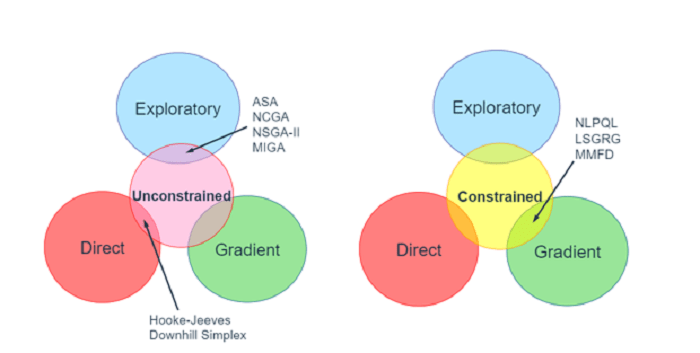
Gradientenmethoden: Sie sind die ältesten und wurden in der Branche gut getestet. Sie arbeiten nach dem Prinzip minimaler Energie oder maximaler Stabilität. Sie lassen einen Ball sanft in ein Tal fallen, und er gleitet den Weg mit dem steilsten Abstieg entlang, bis er den tiefsten Punkt in seiner Nähe erreicht. Diese Methoden funktionieren im kontinuierlichen Designraum, der C0- und C1-Kontinuität aufweist. Da sie wahrscheinlich in den lokalen Minima stecken bleiben, sollte der Ausgangspunkt sorgfältig ausgewählt werden.

Direkte Methoden: Ein direkter Suchalgorithmus beginnt mit einem Basispunkt. Es durchsucht eine Reihe von Punkten in der Umgebung und sucht nach einem Punkt, bei dem der Wert der Zielfunktion niedriger ist als der aktuelle. Der Algorithmus springt zu diesem Punkt als neuen Basispunkt und sucht nach einer neuen Menge von Punkten um ihn herum. Man kann sich vorstellen, dass eine solche Methode recheneffizient ist, da keine Gradientenberechnung erforderlich ist. Es ist vielseitiger, da keine C0- und C1-Kontinuität erforderlich ist. Die häufigsten sind Hooke's-Jeeves und Downhill Simplex.
Die Hooke's Jeeves-Methode verfolgt die Bewegungsrichtung. Es ändert seine Richtung nicht bei jedem Schritt, wenn in Fahrtrichtung ein tieferer Punkt verfügbar ist.

Explorative Methoden: Diese Methoden basieren auf Kreuzungs- oder Mutationstechniken zwischen einem Datensatz von Punkten, die als Eltern bezeichnet werden, um einen anderen Datensatz von Punkten zu erzeugen, die als Kinder bezeichnet werden. Der neue Datensatz entwickelt sich mit jeder Mutation weiter und nähert sich der optimalen Lösung. Dies ist ein High-Fidelity-Schema, das mit allen Arten von Zielfunktionen funktioniert: diskontinuierlich, nicht differenzierbar, stochastisch, gemischt ganzzahlig und stark nichtlinear mit mehreren Spitzen und Tälern, wie unten gezeigt. Allerdings ist es im Hinblick auf den Rechenaufwand das teuerste Optimierungsschema. Die gebräuchlichsten Methoden sind genetische Algorithmen, Partikelschwarm und adaptives simuliertes Annealing.
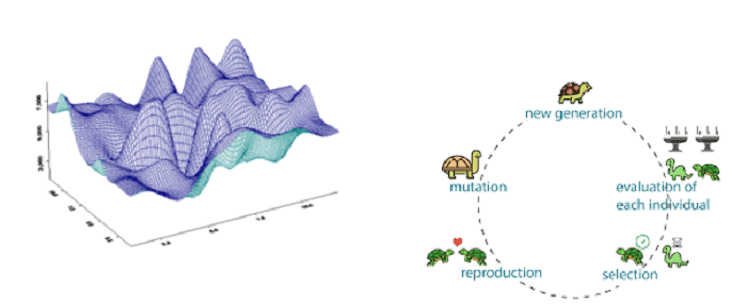
Zeigerbasierte Methoden: Dies ist ein Mix-and-Match-Ansatz für den Fall, dass der Benutzer keine Ahnung hat, welche Art von Technik am besten geeignet wäre, um das Problem mit angemessener Genauigkeit zu lösen. Der Zeigeransatz kann hilfreich sein, wenn der Benutzer auf eine unbekannte Art von Designraum stößt, der schwer zu visualisieren ist. Die Zeigermethode kann bis zu drei Optimierungsschemata verwenden, vorzugsweise eines aus jedem Korb: Gradient, direkt und explorativ. Während die Optimierung voranschreitet, verfolgt der Algorithmus die Wirksamkeit jeder Methode und verwendet diejenige, die für das gegebene Problem am besten geeignet ist.
Treten Sie dem Forum für Designer bei!
Ihr Fachwissen ist wichtig für die Gemeinschaft. Helfen Sie uns und bringen Sie Ihr Wissen ein!
Jetzt dem Forum beitretenTauschen Sie sich aus, lernen Sie und wachsen Sie mit den besten Fachleuten der Branche.

