Treten Sie dem Forum für Designer bei!
Ihr Fachwissen ist wichtig für die Gemeinschaft. Helfen Sie uns und bringen Sie Ihr Wissen ein!
Jetzt dem Forum beitretenTauschen Sie sich aus, lernen Sie und wachsen Sie mit den besten Fachleuten der Branche.
Die Größe und Komplexität von Produktdesigns, die mit Abaqus – einer Finite-Elemente-Analyse (FEA) und Multiphysik-Simulationssoftware – analysiert und getestet werden, nimmt ständig zu. Die Submodellierung ist eine effektive Technik, die eingesetzt werden kann, wenn detaillierte Produktsimulationsergebnisse für einen kleinen, lokalisierten Bereich innerhalb eines größeren Modells benötigt werden, und die es dem Analysten ermöglicht, die Rechenanforderungen und die Laufzeit einer Analyse erheblich zu reduzieren.
Eine globale Analyse einer Struktur kann zunächst dazu verwendet werden, Bereiche zu identifizieren, in denen die Reaktion auf die Belastung kritisch ist. Für die kritischen Bereiche kann dann ein lokales Teilmodell mit einer verbesserten geometrischen Darstellung und/oder Netzverfeinerung erstellt werden. Dieses lokale Teilmodell bietet eine höhere Genauigkeit als das globale Modell, ohne dass das gesamte Modell neu vernetzt und analysiert werden muss. Dieser Ansatz führt zu geringeren Analysekosten bei gleichzeitiger Beibehaltung ausreichender Details in kritischen Regionen.
In diesem Blog werden wir uns mit der Theorie hinter der Submodellierung, den beiden in Abaqus verfügbaren Submodellierungstechniken und der Implementierung von Submodellen befassen. Wir werden auch die Grenzen der Submodellierung in Abaqus und den wichtigen Schritt der Verifizierung der Analyseergebnisse beleuchten.
Theorie der Submodellierung
Die Submodellierung in Abaqus nutzt das Saint-Venant-Prinzip, bei dem die Grenze des Submodells weit genug von der interessierenden Region innerhalb des Submodells entfernt ist, um die angewandten Kräfte durch äquivalente lokale Kräfte ersetzen zu können. Die globale Modelllösung wird verwendet, um das Verhalten der Submodellgrenze durch die Steuerung von angetriebenen Variablen zu definieren, die für die aufgebrachten Kräfte repräsentativ sind. Die Lösung im interessierenden Bereich wird durch die Endwirkungen nicht verändert, solange die Endlasten statisch äquivalent bleiben.
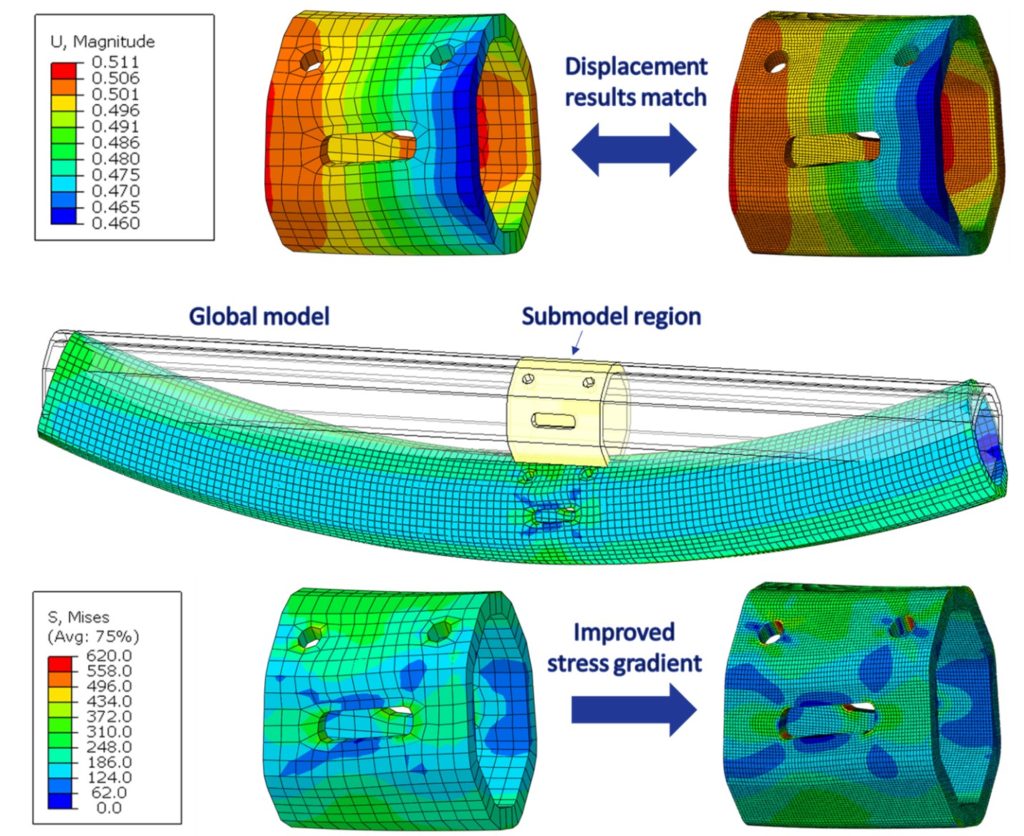
In Abbildung 1 ist ein Beispiel für einen Träger mit mehreren lokalisierten Öffnungen dargestellt. Das globale Modell des Vollträgers wird verwendet, um die angetriebenen Variablen als Ausgabe an den gemeinsamen Grenzen für das Teilmodell zu bestimmen und erleichtert die Verwendung eines relativ groben Netzes. Die Analysen werden unabhängig voneinander für das globale Modell und das Teilmodell durchgeführt, wobei die angetriebenen Variablen die einzige Verbindung zwischen den beiden Modellen darstellen. Dank dieser Unabhängigkeit können Sie geometrische Merkmale, Elementtypen, Materialeigenschaften usw. flexibel ändern, um die Darstellung der untermodellierten Region zu verbessern. Wie bei jeder Modellierungstechnik ist es wichtig, die Ergebnisse zu validieren, um sicherzustellen, dass sie physikalisch sinnvoll sind. Ein Vergleich von Konturdiagrammen in der Nähe der Grenzen der submodellierten Region des Gesamt- und des Teilmodells kann verwendet werden, um die Konsistenz der Ergebnisse zu bestätigen.


Submodellierungstechniken in Abaqus
In Abaqus gibt es zwei Techniken für die Submodellierung, die als knotenbasierte und oberflächenbasierte Submodellierung bezeichnet werden. Bei der knotenbasierten Technik wird das Knotenergebnisfeld aus dem globalen Modell auf die Knoten des Submodells interpoliert; dies ist die allgemeinere und am häufigsten verwendete Technik. Im Gegensatz dazu wird bei der oberflächenbasierten Submodellierung das Spannungsfeld auf die Integrationspunkte der Submodelloberfläche interpoliert. Die oberflächenbasierte Submodellierung ist auf Solid-to-Solid-Anwendungen und statische Analysen beschränkt, für alle anderen Zwecke sollte die knotenbasierte Submodellierung verwendet werden. Je nach den Eigenschaften des Modells können beide Techniken oder eine Kombination aus beiden in einer Analyse verwendet werden.
Die oberflächenbasierte Technik kann genauere Spannungsergebnisse liefern, wenn in einer statischen Analyse ein signifikanter Unterschied in der durchschnittlichen Steifigkeit in der Region des Submodells besteht und das globale Modell einer kraftgesteuerten Belastung unterliegt. Wenn hingegen die Steifigkeit in den Regionen vergleichbar ist, liefert die knotenbasierte Submodellierung ähnliche Ergebnisse wie die oberflächenbasierte Submodellierung, wobei das Potenzial für numerische Probleme, die durch Starrkörpermodi verursacht werden, reduziert wird. Unterschiede in der Steifigkeit können durch zusätzliche Details im Teilmodell, wie z.B. Öffnungen oder Verrundungen, oder durch geringfügige geometrische Änderungen entstehen, die eine erneute Durchführung der globalen Analyse nicht rechtfertigen.
Wenn das Modell großen Verschiebungen oder Drehungen unterworfen ist, kann die knotenbasierte Teilmodellierung die Genauigkeit bei der Übertragung großer Verschiebungen und Drehungen auf das Teilmodell verbessern. Abhängig von den Ergebnissen, die von größtem Interesse sind. Die knotenbasierte Submodellierung bietet eine genauere Übertragung des Verschiebungsfeldes in das Submodell. Die flächenbasierte Submodellierung hingegen liefert eine genauere Übertragung des Spannungsfeldes, was zu einer genaueren Bestimmung der Reaktionskräfte im Submodell führt. Die beiden Techniken können innerhalb eines einzigen Modells an unterschiedlichen Grenzen eingesetzt werden.
Implementieren Sieing Abaqus Teilmodelle
Das lokale Modell kann über die in der Ausgabedatenbankdatei (im ODB- oder SIM-Format) gespeicherten Daten gesteuert werden. Knotenbasierte Submodelle können auch über die Ergebnisdatei (.fil) gesteuert werden. Nur die Variablen, die in die Ausgabedatenbank geschrieben wurden, werden im Teilmodell verwendet, daher ist es wichtig, die Ausgabedaten in ausreichender Häufigkeit zu speichern. Diese Ergebnisse müssen im globalen Koordinatensystem gespeichert werden, damit sie in das Teilmodell interpoliert werden können. Im Falle von Nodaldaten werden die Werte immer in Bezug auf die globalen Richtungen in die Ausgabedatenbankdatei geschrieben, unabhängig davon, ob Nodalkoordinatentransformationen verwendet werden. Alle angetriebenen Variablen sollten während der globalen Analyse mit einer gemeinsamen Frequenz gespeichert werden, und diese Frequenz sollte fein genug sein, um eine angemessene Reproduktion des globalen Zeitverlaufs für die angetriebenen Variablen zu ermöglichen. Wenn die Ergebnisse mit unterschiedlichen Frequenzen gespeichert werden, wird die gröbste Frequenz in der Teilmodellanalyse verwendet. Es wird empfohlen, ein einziges Set zu erstellen, das alle Knotensets und/oder Elementsets enthält, von denen das Submodell gesteuert werden soll. In Abbildung 2 ist das Set, das die Grenze des Teilmodells definiert, rot hervorgehoben und mit folgender Bezeichnung versehen Submodell-Region.

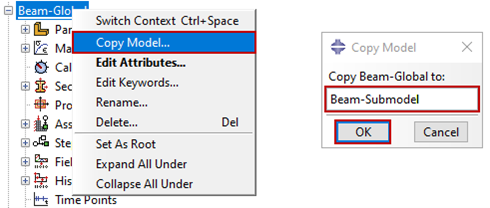
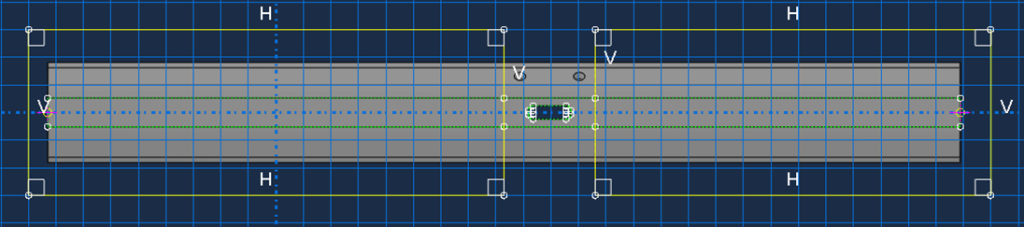
Alle Arten von Belastungen und vorgeschriebenen Randbedingungen können auf das Teilmodell angewendet werden. Sie sollten jedoch darauf achten, dass die Lasten und Randbedingungen im Teilmodell so angewendet werden, dass sie mit dem globalen Modell übereinstimmen, um falsche Ergebnisse zu vermeiden. Nur die angetriebenen Variablen werden interpoliert und in das Teilmodell übertragen. Alle vordefinierten Felder müssen so bereitgestellt werden, wie sie im globalen Modell waren. Die Anfangsbedingungen sollten zwischen dem globalen Modell und dem Teilmodell konsistent sein. Der Einfachheit halber kann es hilfreich sein, das ursprüngliche globale Modell zu kopieren, um das Teilmodell zu erstellen (Abbildung 3). Verwenden Sie die Werkzeuge zum Erstellen von Schnitten, um Material außerhalb der Grenzen des Teilmodells zu entfernen, wie in Abbildung 4 gezeigt. Auf diese Weise können Sie die Einstellungen des globalen Modells beibehalten und die Gefahr von Fehlern bei der Erstellung des Teilmodells minimieren.
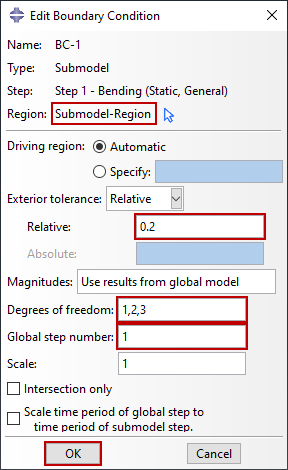
Die Schrittzeit in der Submodell-Analyse sollte mit der Schrittzeit in der globalen Analyse übereinstimmen, sonst ist die Interpolation in Bezug auf die Zeit nicht korrekt. Wenn es eine Diskrepanz gibt, kann die Zeitspanne des globalen Schritts auf die des Submodells skaliert werden, indem Sie die Option zu Zeitspanne des globalen Schritts auf die Zeitspanne des Submodell-Schritts skalieren wenn Sie die in Abbildung 5 gezeigten Randbedingungen implementieren.
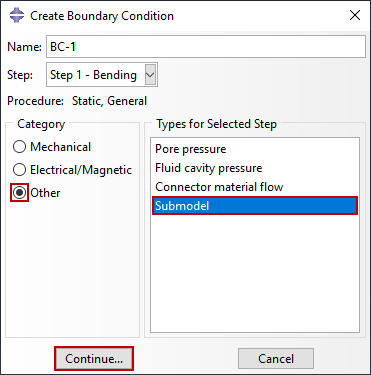
Angetriebene Knoten werden durch die Randbedingungen des Teilmodells definiert. Sie können angeben, welche Freiheitsgrade am Rand des Teilmodells angetrieben werden sollen – normalerweise werden alle Freiheitsgrade an den angetriebenen Knoten angegeben. Zusätzlich zur Skalierung des Zeitraums kann Abaqus gegebenenfalls auch den Wert der angetriebenen Variablen skalieren, die vom globalen Modell auf das Teilmodell angewendet werden. In Abbildung 5 ist eine Randbedingung für ein Submodell implementiert, die alle Freiheitsgrade für feste Kontinuumselemente (1-3) ohne Skalierung enthält. Beachten Sie, dass nur die grundlegenden Lösungsvariablen gesteuert werden können. Bei der Submodellierung von Festkörper zu Festkörper oder von Schale zu Schale umfasst dies Verschiebungen, Temperaturen, elektrisches Potential, Porendruck, usw. Geschwindigkeiten oder Beschleunigungen an der Grenze des Submodells können nicht gesteuert werden. Abaqus wählt die gesteuerten Variablen automatisch aus, wenn ein globales Schalenmodell zur Steuerung eines lokalen Volumenmodells verwendet wird. Andere Randbedingungen für Teilmodelle können wie gewohnt erstellt, geändert oder entfernt werden.

Abaqus interpoliert sowohl räumlich als auch zeitlich, um die Werte der gesteuerten Knotenvariablen während des gesamten Schritts der Submodellanalyse zu bestimmen. Die Reihenfolge der räumlichen Interpolation der gesteuerten Variablen wird durch die Reihenfolge der auf der globalen Ebene verwendeten Elemente bestimmt. Die automatische Zeitinkrementierung wird unabhängig in der globalen und der Submodell-Analyse angewendet. Die unabhängige Zeitinkrementierung wird durch die zeitliche Interpolation der angetriebenen Variablen berücksichtigt. Es wird eine lineare zeitliche Interpolation zwischen den aus der Ausgabedatenbank oder der Ergebnisdatei gelesenen Werten verwendet.
Wenn das globale Modell große Verschiebungen oder Drehungen erfährt, muss der Benutzer sicherstellen, dass das Teilmodell diese Verschiebungen oder Drehungen ebenfalls erfährt. Bei der knotenbasierten Submodellierung berücksichtigen die treibenden Knoten automatisch Verschiebungen und Drehungen, so dass das Submodell relativ zum globalen Koordinatensystem korrekt positioniert wird. Bei der oberflächenbasierten Submodellierung hingegen liefert die ausschließliche Verwendung von Oberflächentraktionen dem Submodell keine Verschiebungsinformationen. Um die Verschiebungen zu berücksichtigen, muss das Teilmodell stattdessen Folgendes enthalten: angewandte Randbedingungen, angetriebene Knoten und Trägheitsrelief. Wenn beide Methoden verwendet werden, ist es wichtig, eine konsistente Fahrmethode für den gesamten ausgewählten Bereich beizubehalten, um zu verhindern, dass durch unvollständige oder übermäßige Fahrdefinitionen Überlastungen entstehen.
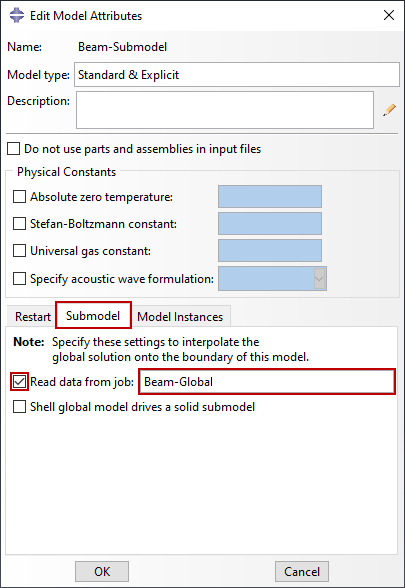
Beim Einrichten eines Teilmodells sollten die Modellattribute so geändert werden, dass sie auf die Ausgabedatenbank oder die Ergebnisdatei verweisen. Die in Abbildung 6 gezeigten Modellattribute würden Abaqus veranlassen, die Beam-Global.odb Ausgabedatenbankdatei und verwenden Sie diese Ergebnisse in einer Analyse eines Teilmodells, das in der Beam-Submodel.inp Eingabedatei.
Beschränkungen der Submodellierung
Es gibt einige Einschränkungen bei den Methoden und Elementtypen, die mit dem Submodellierungsansatz kompatibel sind. Diese Einschränkungen werden hier kurz umrissen. Weitere Informationen dazu finden Sie in der Dokumentation.
Die Elemente, die auf globaler und Submodellebene verwendet werden können, sind auf dreieckige und viereckige Kontinuums-, Schalen- oder Membranelemente erster und zweiter Ordnung sowie auf tetraedrische, keilförmige oder gemauerte Kontinuumselemente erster und zweiter Ordnung beschränkt. Globale Modelle können sowohl Volumen- als auch Schalenelemente enthalten, wobei alle angetriebenen Knoten innerhalb der Schalenelemente im globalen Modell liegen müssen.
Die Randknoten des Submodells dürfen nicht in Regionen des globalen Modells liegen, in denen nicht genügend Informationen für die Interpolation der angetriebenen Variablen vorhanden sind. Dazu gehören Regionen, in denen es nur eindimensionale Elemente (wie Balken, Fachwerke, Glieder oder achsensymmetrische Schalen), Benutzerelemente, Unterstrukturen, Federn, Dashpots, andere spezielle Elemente oder achsensymmetrische Elemente gibt.
Bei der Verwendung von Schalenelementen sollten Schalenelemente mit fünf Freiheitsgraden pro Knoten (S4R5, S8R5 usw.) in der Regel auf globaler Ebene vermieden werden, da die Drehungen nicht gespeichert werden. Diese Elemente können nicht für die Submodellierung von Schalen in Solids verwendet werden.
Submodelle können nicht in gekoppelten thermisch-elektrischen, gekoppelten thermisch-elektrochemischen und modusbasierten linearen Dynamikverfahren verwendet werden. Die oberflächenbasierte Submodellierung kann nur in allgemeinen statischen Verfahren verwendet werden. Shell-to-solid-Submodellierung kann nicht zusammen mit einer anderen Art von Submodellierung im selben Modell verwendet werden.
Verifizierung von Ergebnisse der Analyse
Bei der Verwendung des Submodellierungsansatzes erhält man anschließend zwei Sätze von Analyseergebnissen: den ersten aus einem globalen Modell, das eine Annäherung an das Verhalten liefert, und den zweiten aus einem verfeinerten lokalen Modell, das eine genauere Darstellung der detaillierten Ausgabe liefert. Ein wichtiger Schritt im Submodellierungsverfahren ist die Überprüfung der Ergebnisse. In Abbildung 7 sind die Ergebnisse eines knotenbasierten Teilmodells dargestellt. Das Modell wird zunächst auf die Konsistenz der Verschiebungen in der Region des Submodells überprüft, bevor der Spannungsgradient aufgetragen wird. Wenn größere Abweichungen bei den Verschiebungen festgestellt werden, wirkt sich dies auf alle nachfolgenden Ergebnisse aus und das Modell sollte überprüft und erneut eingereicht werden. Sobald die Verschiebungen übereinstimmen, können andere Ergebnisse wie die Spannungen abgefragt werden. Hier wird eine Verbesserung des Spannungsgradienten erreicht, indem die Netzdichte in der untermodellierten Region erhöht wird. Die Spannungen in anderen Regionen des Trägers können aus dem globalen Modell entnommen werden, in dem das grobe Netz ausreicht, wenn keine spannungskonzentrierenden Öffnungen vorhanden sind.
Treten Sie dem Forum für Designer bei!
Ihr Fachwissen ist wichtig für die Gemeinschaft. Helfen Sie uns und bringen Sie Ihr Wissen ein!
Jetzt dem Forum beitretenTauschen Sie sich aus, lernen Sie und wachsen Sie mit den besten Fachleuten der Branche.

