Résolution des équations gonimétriques

[Luigi_72]

Bonjour à tous
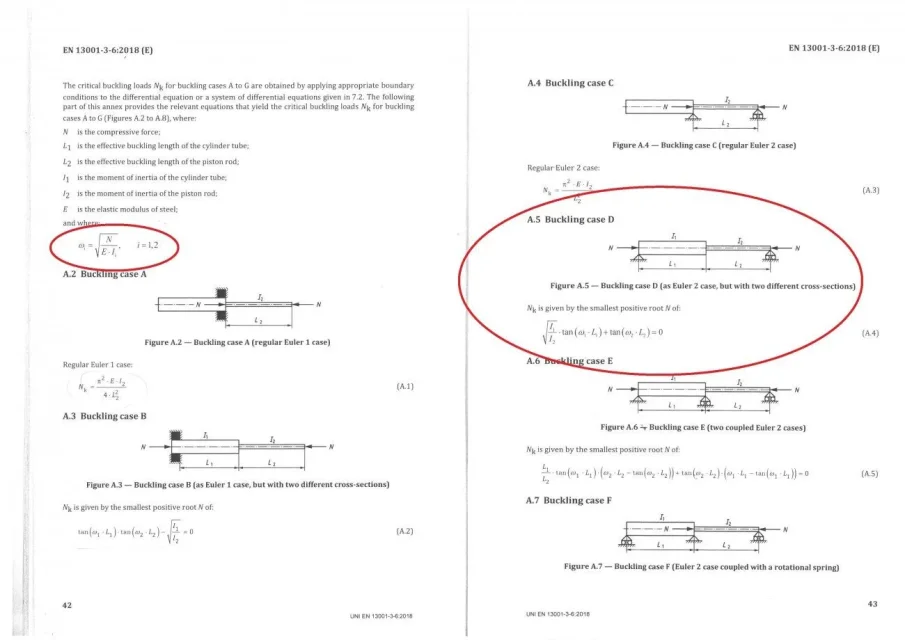
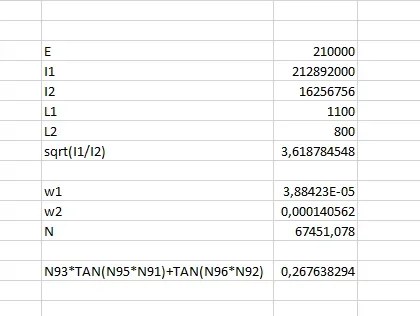
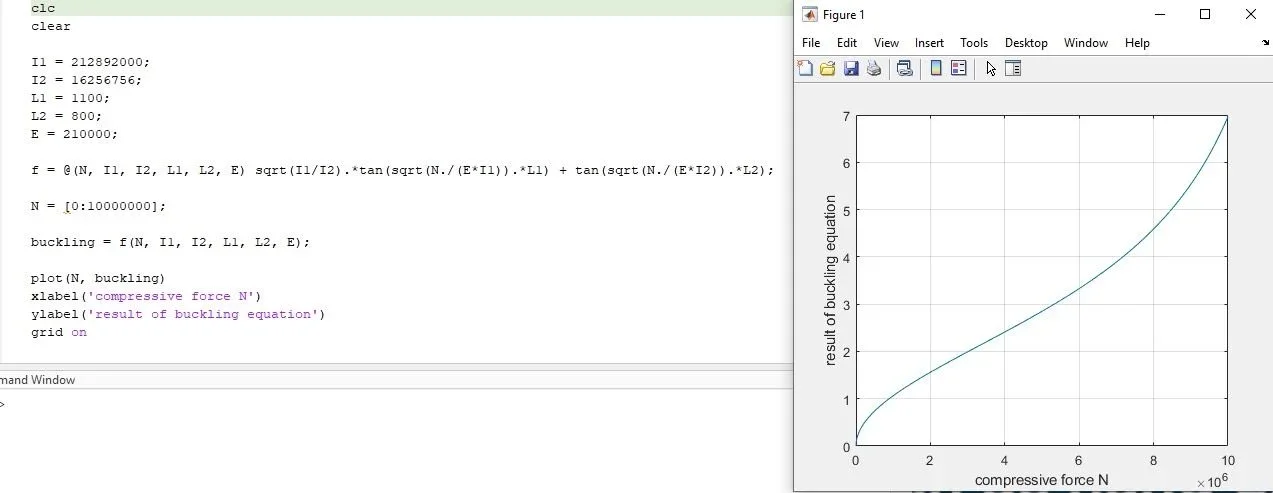
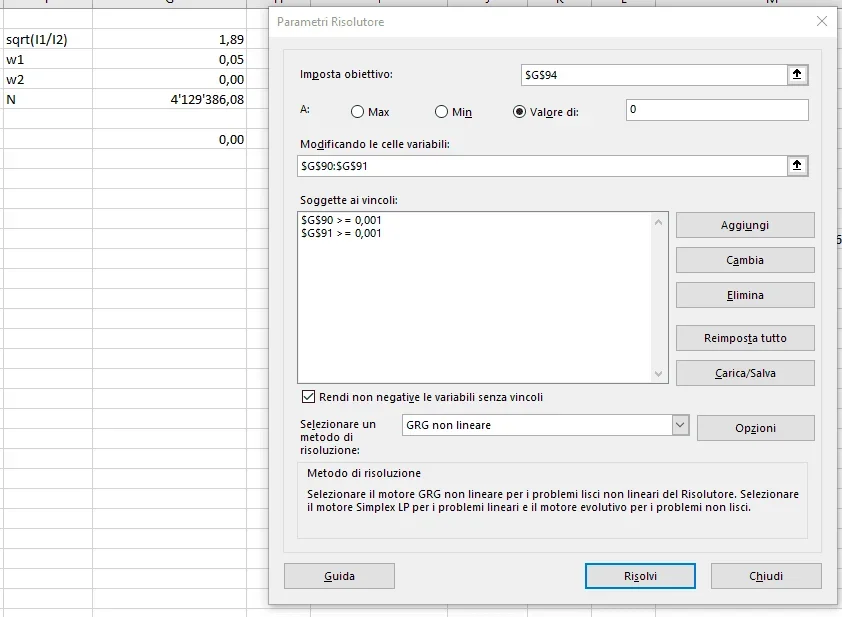
J'ai réalisé que j'étais rouillée et beaucoup depuis que j'ai fréquenté l'université et je ne peux pas résoudre cette question mathématique même si je dois calculer la charge de pointe sur une tige d'un piston. Je porte la formule dans le fichier ci-joint, je dois trouver "n".cette formule fait partie du traitement du flambeau déclaré dans la norme 13001-3-6 sortie en juillet. même si j'existe un autre n moyens de résoudre les questions sur la charge de pointe je dois adhérer à la norme: fou:.


a Merci à l'avance à ceux qui voudront passer du temps.

 

[exxon]

n = w^2 (e-ii)

 

[Luigi_72]

n = w^2 (e-ii)

Merci pour la réponse.
Mais je ne comprends pas, la formule rouge-circulaire dans l'annexe gaucher est ce que vous me ramenez. Vous avez obtenu n selon les autres paramètres, mais le problème est la bonne équation.
Peut-être que je n'étais pas clair, je sais.
II 1e2
et
♪

mais pas wi et donc n

 

[volaff]

Au revoir.
Où as-tu trouvé cet extrait ?

 

[meccanicamg]

le système le plus simple pour résoudre l'équation de droite est de remplacer les membres et par l'équation de gauche, puis d'obtenir n.

le système le plus rapide est d'utiliser excel et d'écrire les deux formules. activez le résolveur comme module supplémentaire et faites la solution pour vérifier l'équation... sans démonter l'équation pour trouver l'inverse.
Une autre alternative est d'utiliser l'alpha de loup en ligne et de lui faire trouver la formule inverse.

 

[Luigi_72]

Au revoir.
Où as-tu trouvé cet extrait ?

Bonjour.

fait partie de la règle 13001-3-6:2018

 

[Luigi_72]

Merci pour les conseils mais je vous demande si vous pouvez lire ci-dessous parce que je ne peux toujours pas tout faire carrément.

le système le plus simple pour résoudre l'équation de droite est de remplacer les membres et par l'équation de gauche, puis d'obtenir n.
J'ai gardé comme ça, mais je suis toujours désolé. Je dois essayer la route que vous avez indiquée ci-dessous.le système le plus rapide est d'utiliser excel et d'écrire les deux formules. activez le résolveur comme module supplémentaire et faites la solution pour vérifier l'équation... sans démonter l'équation pour trouver l'inverse.
Je cherchais une telle solution, mais je n'ai jamais utilisé excelle comme ça. Vous pourriez me donner un exemple, s'il vous plaît. Une autre alternative est d'utiliser l'alpha de loup en ligne et de lui faire trouver la formule inverse.

jamais utilisé

 

[Luigi_72]

J'ai essayé de résoudre l'équation avec excellent à travers le résolveur mais ce n'est pas bon. C'est probablement la tangente qui s'exprime dans les rayons qui me cause des ennuis.

 

[volaff]

Bonjour.
Pourriez-vous m'envoyer cette règle ou est-ce un problème ?

 

[Luigi_72]

la norme se compose de plusieurs pages et ne peut pas être copié mais si vous avez besoin d'une partie en particulier, je peux vous envoyer quelque chose.

 

[volaff]

Ok, je vais te le prendre.
Je vous remercie.

 

[giaigimail]

Salut à tous, je vous demande si vous avez des mises à jour car je me trouve les mêmes problèmes merci!

 

[ANR4949]

J'ai essayé de résoudre l'équation avec excellent à travers le résolveur mais ce n'est pas bon. C'est probablement la tangente qui s'exprime dans les rayons qui me cause des ennuis.

pour moi excell donne ce résultat Luigi.

 

[giaigimail]

pour moi excell donne ce résultat Luigi.

Bonjour, je vous demande si vous imposez une valeur de départ pour n

 

[ANR4949]

Bonjour, je vous demande si vous imposez une valeur de départ pour n

Salut, pas de valeur, je mets la cellule vide et je la sélectionne dans le solveur comme un but.
s'il ne fonctionne pas ainsi vous pouvez également le mettre à zéro, puis il change avec les itérations du solveur.

 

[giaigimail]

Salut, pas de valeur, je mets la cellule vide et je la sélectionne dans le solveur comme un but.
s'il ne fonctionne pas ainsi vous pouvez également le mettre à zéro, puis il change avec les itérations du solveur.

Bonjour.

Vous définissez alors la cellule correspondant à n comme cible ? Et l'équation avec des tangents comme la tracer ? Il y a quelque chose qui me manque

 

[giaigimail]

Bonjour.

Vous définissez alors la cellule correspondant à n comme cible ? Et l'équation avec des tangents comme la tracer ? Il y a quelque chose qui me manque

J'ai essayé d'insérer vos résultats dans excel, mais l'équation de bûcher n'est pas vérifiée devant être égale à zéro.

si je change n la seule solution proposée est n=0. boh?

 

[Stan9411]

Il est facile de voir que l'équation de droite n'est jamais égale à zéro, exprimant w1 et w2 selon n, à travers l'équation de gauche. Il est clair que le soluteur d'excel est empilé.
matlab pour ces opérations mathématiques simples a la même syntaxe que excel pour que vous compreniez.

 

[giaigimail]

J'ai probablement tort, mais à partir du graphique que vous avez tracé, l'équation a tendance à zéro pour n=0. le problème posé par la norme est d'obtenir nk qui est la force de compression critique comme la plus petite racine positive de l'équation à droite (annotation1.png attachée).

J'ai pensé, mais toujours probablement mal, à changer w1 et w2 dans le soluteur en définissant comme objectif d'annuler l'équation a4 comme l'exige la norme. Une fois que vous calculez le wi à partir du moins des deux, vous obtenez le nk requis. le doute est que j'ai assigné comme une contrainte qui wis sont plus ou égal de 0,001 assez arbitrairement. (Note 2.png jointe). note que les valeurs ne sont pas les mêmes que le problème, mais que les formules sont les mêmes.
merci à tous pour l'attention et la patience

 

[Stan9411]

Vous devez venir par force la même chose ... en exprimant n dans la bonne équation, ou en calculant les racines de la bonne équation et puis en les utilisant pour calculer n ... est l'algèbre .. il n'est pas possible que d'une manière vous trouvez la solution et dans l'autre non.

Il est clair qu'il n'y a pas de flambeau. est la solution triviale classique