Je répète, en soulignant que les insultes d'étrangers glissent au-dessus de moi. sont si quelque chose d'intéressant pour voir les réactions d'une certaine partie de la modération du site qui utilise plus de poids et plus de mesures. De toute façon...
nous venons plutôt à la partie technique, beaucoup plus intéressant.
dire d'un outil qui gère 2^64 chiffres (plus de 18 milliards) qui est bon pour le shopping, cela signifie que lorsque vous avez utilisé la règle ou les tables numériques vous pesiez 4 atomes d'oxygène avec la stadera.
voir, si vous êtes convaincu qu'excellent "gestion" 2^64 chiffres... Alors il est clair pourquoi vous ne pouvez pas comprendre le sens de mes interventions. Malheureusement (pour vous), ces 64 bits sont utilisés pour stocker des variables de manière beaucoup plus complexe qu'un simple codage binaire.
Je doute que vous soyez intéressé, mais au cas où vous devriez chercher iee 754, nous, Européens, avons accepté de dire iec 60559:1989. Vous constaterez que l'amplitude des valeurs qui peuvent être représentées avec ces 64 bits est beaucoup plus large que vous ne le croyez (d'environ 10^-308 à 10^308), mais vous pouvez aussi voir que ce n'est pas le seul paramètre à prendre en compte, et surtout que la précision n'a rien à voir avec le nombre ci-dessus.
pour ceux qui s'intéressent vraiment à la question, donnons quelques informations d'une certaine valeur.
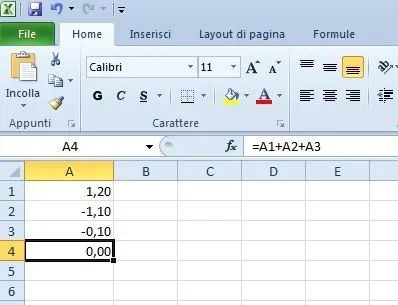
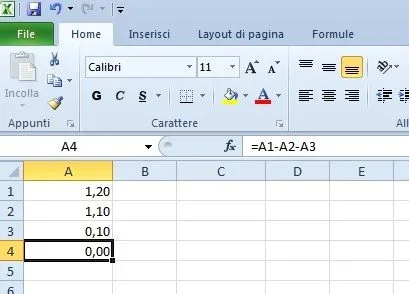
Comme je l'ai mentionné plus haut, le problème excel est le stockage de toutes les variables au format de données unique, les virgules mobiles 64 bits (le « double » des langages de programmation). afin d'éviter que, dans les calculs comptables (travaux des feuilles de calcul), la représentation dans les virgules mobiles crée des nombres "pas complets", chaque cellule contient un système de représentation arrondi distinct, qui satisfait l'œil du comptable.
il va sans dire que ce système de calcul et de visualisation très peu s'adapte au calcul scientifique, mais plus semble l'ignorer. tous les langages de programmation, et les programmes de calcul purement scientifiques (voir matlab ci-dessus), permettent plutôt le choix du type de variable selon son utilisation. Le choix qui reste en charge du programmeur qui, bien sûr, doit savoir ce qu'il fait.
excel cache ces "questions" en simplifiant l'approche du calcul numérique, un peu comme l'arduino cache tous les problèmes du design "encastré", ce qui permet à tout le monde de stupéfier les amis et les proches avec quelques effets spéciaux.
microsoft ne cache pas les limites de l'excel, en effet, écrit des articles avec des titres complètement sans équivoque
"l'arithmétique en points flottants peut donner des résultats inexacts en excellent".
articles dans lesquels il admet également que leur système de stockage mobile suit les spécifications iee 754 "presque entièrement". dans ses documents décrit également comment certains chiffres sont "adaptés" en ce moment pour réduire (à leur avis...) les erreurs les plus évidentes.
Il faut dire que le problème de base (pas les "adaptations" ci-dessus) n'est pas la faute d'excel, mais c'est un comportement prévisible du système d'encodage dans les virgules mobiles. un calcul exécuté avec excel ou avec un programme différent qui stocke des données sur des variables avec un codage identique, donnera les mêmes résultats. le "colpa" est de ne pas avoir d'autres codifiches (entier, décimal, etc.) et de cacher ce besoin à l'utilisateur qui croit être inutile (voir commentaires précédents).
Faisons un exemple : si nous évaluons l'expression
(a + b + c )
avec
= 1,2
b = 1.1.1
= -0,1
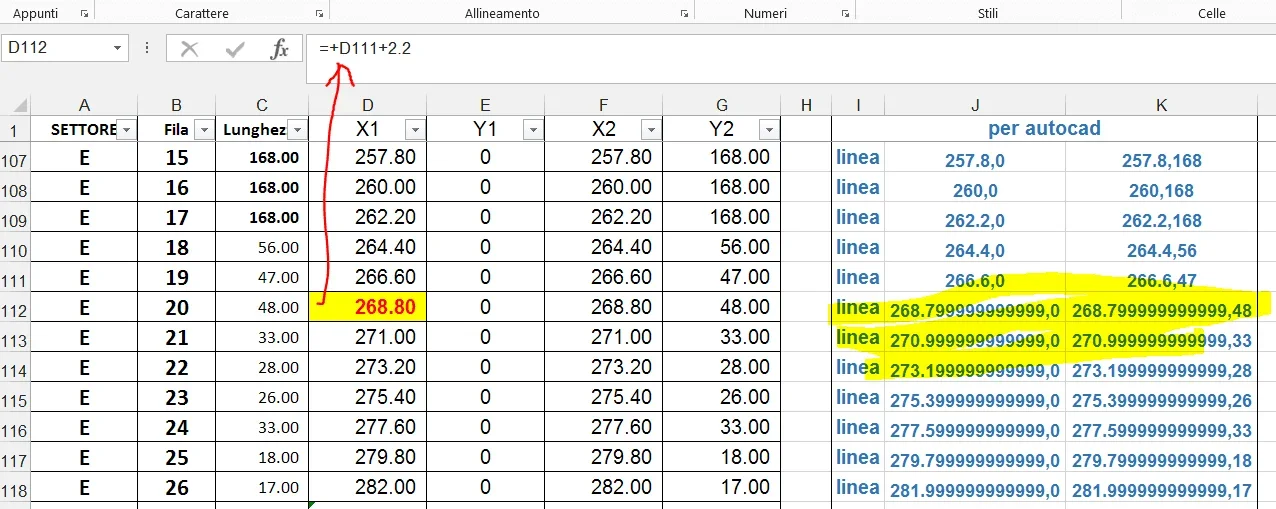
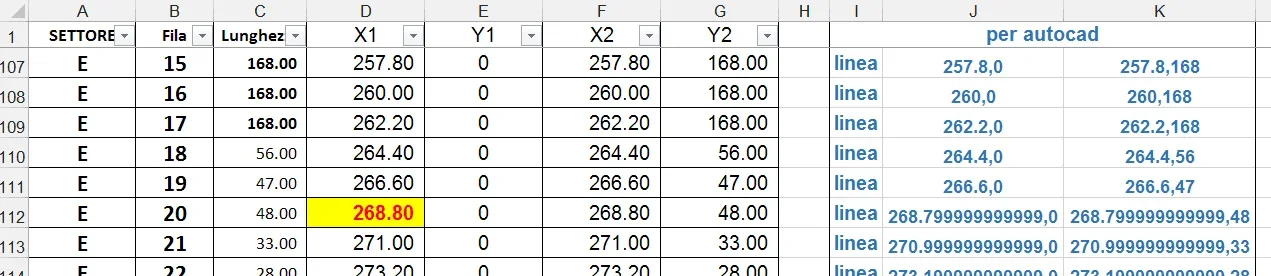
il est facile de faire le calcul "en tête" et d'affirmer que le résultat est zéro. Essayons avec excel
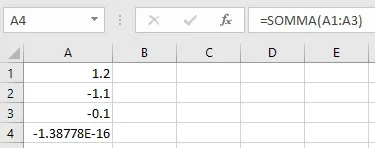
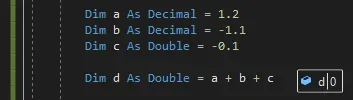
L'erreur est évidente. nous essayons la même chose dans vb.net
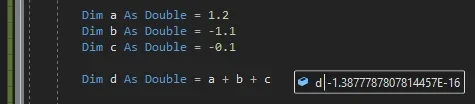
utilisant le même type de variables (double), le résultat est le même.
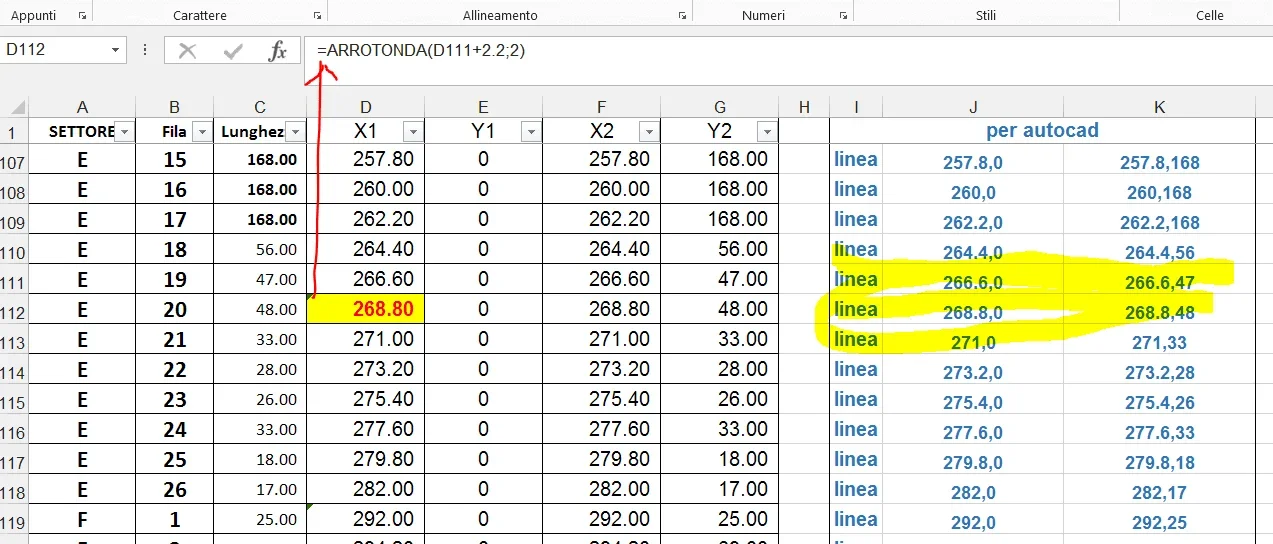
Il suffit, cependant, d'utiliser un type différent de variable (décimale) pour les nombres... incriminés, et le résultat devient ce que vous devez attendre.
un avant-dernier commentaire pour ceux qui diront que d'une erreur de 10^-16 ils se soucient parce qu'il est petit: l'erreur doit être évaluée par rapport à la vraie valeur, pas en termes absolus. Si d'une opération j'attends une valeur de 2x10^-16 et je me trouve une erreur de 1x10^-16, l'erreur est 50%.
un dernier commentaire pour ceux qui diront qu'ils travaillent avec des compteurs et des kilogrammes et celui de petites valeurs ne sont pas intéressants: si le résultat d'une de ces opérations doit être multiplié par le nombre d'avogadro (6.022x10^22) ou divisé par la charge de l'électron (1.602x10^-19), l'erreur ne serait plus si insignifiante. . . .
Je conclus en soulignant que tout ce qui précède ne signifie pas que l'excel ne doit pas être utilisé, mais que ses limites doivent être connues avant de se confier comme si c'était le nirvana du calcul automatique, parce qu'il ne l'est pas. se demande pourquoi dans les cellules apparaissent "magiquement" des nombres inattendus est une indication de ne pas avoir clair les limites d'utilisation de cet outil. C'est ce que je pense être mal, pas son utilisation.