Surface et vitesse inclinées

[Fulvio Romano]

J'ai besoin d'aide, mais j'ai honte.

Nous avons une balle sur une surface en pente. Si le plan est clair, je vais prendre du temps. Si la surface est courbée, je la mettrai ? Encore ? Moins ? et la friction avec l'air comment cela affecte-t-il la chose?

Intuitivement, j'ai supposé que, compte tenu de la friction avec l'air, le plan incliné est la route la plus courte parce que celle qui maintient une vitesse moyenne inférieure et donc globalement moins d'énergie gaspillée.
J'ai essayé de calculer mathématiquement l'équation horaire selon la surface, mais je me suis perdu dans les calculs.
J'ai essayé de calculer mathématiquement l'équation de l'énergie, mais rien ne sort.
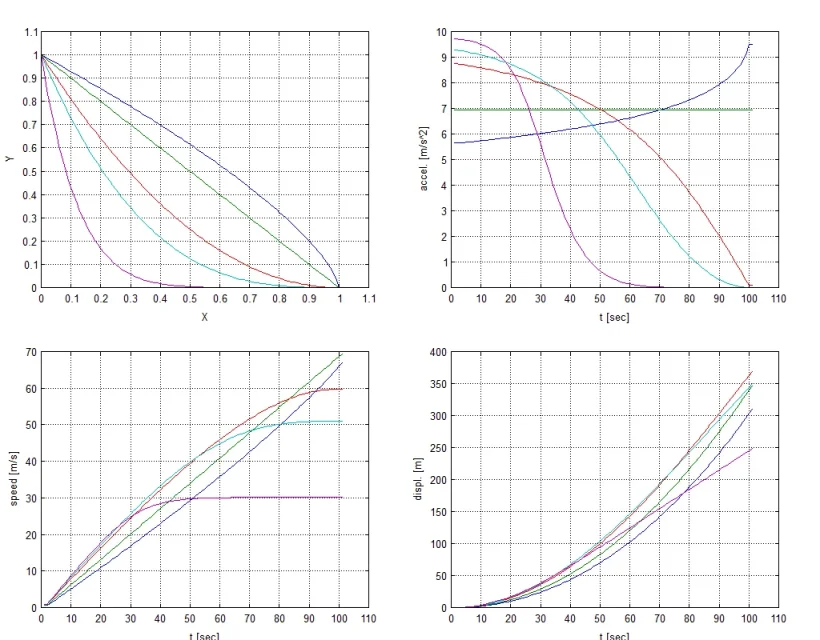
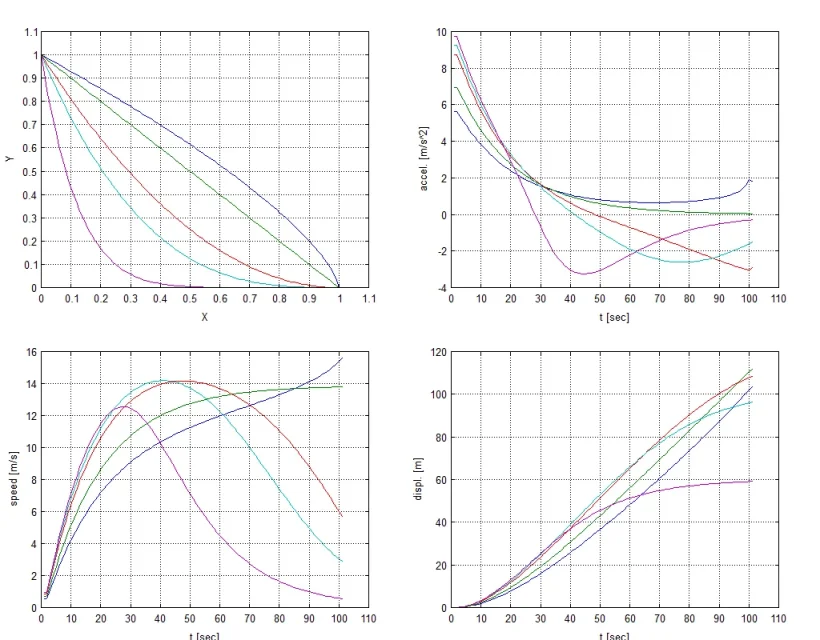
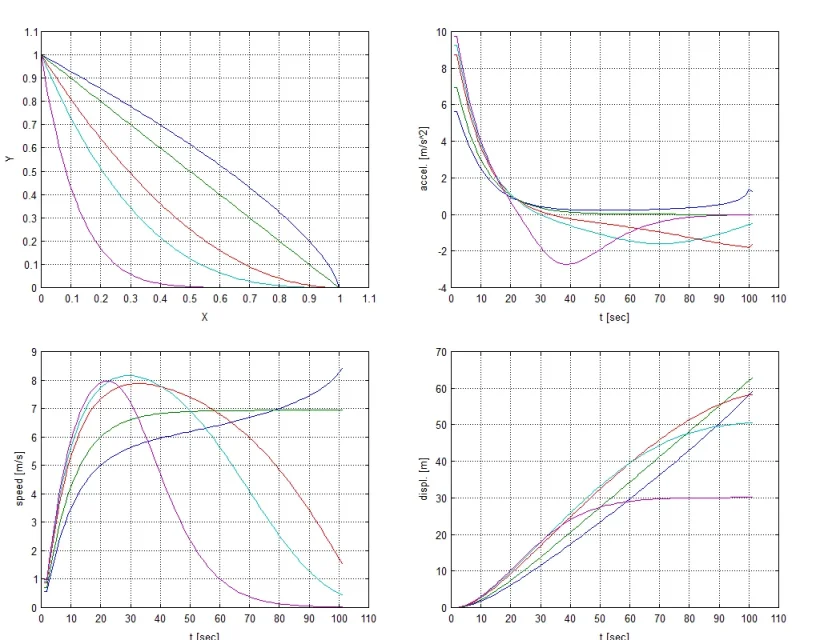
Finalement, en tant que moyeu mécanique, j'ai fait une simulation en matlab. Je confirme que par un coefficient de viscosité élevé la meilleure façon est droite, mais avec la viscosité rien n'existe plus vite lorsque la surface commence à courber, puis retourne désavantageux.

vous voyez les simulations avec sigma égal à 0, 5 et 10. dans chaque diagramme, vous pouvez voir la surface coulissante, l'accélération, la vitesse et la position.

Qui m'aide à mieux comprendre ce phénomène ?

 

[ceschi1959]

Ciao _ ,

alors...

brachistocrone

 

[Fulvio Romano]

Ciao _ ,

alors...

brachistocrone

Ecoute, mec, je t'ai dit de résoudre mon problème, pas en créer un autre !! !

:

 

[Stan9411]

Il est clair que le plan incliné est la route la plus courte, mais c'est aussi celle qui offre un angle sans fin à la seule source d'accélération ou de gravité. au contraire une surface très raide au départ qui se redresse horizontalement très près du sol, permettra à la balle d'atteindre une grande vitesse de pointe, mais affectera une route plus longue et par conséquent viendra de toute façon après. Le compromis est au milieu. il y aura une trajectoire assez courte mais en même temps assez encline à minimiser le temps de déplacement.

Il semble assez intuitif.. et si vous l'avez simulé, vous devez l'avoir compris. Sinon, quel modèle mathématique avez-vous écrit ?

 

[cacciatorino]

peut-être la variable non considérée est l'énergie cinétique stockée par la sphère sous le signe de la rotation autour de son axe baricentrique.

 

[Fulvio Romano]

Il est clair que le plan incliné est la route la plus courte, mais c'est aussi celle qui offre un angle sans fin à la seule source d'accélération ou de gravité. au contraire une surface très raide au départ qui se redresse horizontalement très près du sol, permettra à la balle d'atteindre une grande vitesse de pointe, mais affectera une route plus longue et par conséquent viendra de toute façon après. Le compromis est au milieu. il y aura une trajectoire assez courte mais en même temps assez encline à minimiser le temps de déplacement.

Il semble assez intuitif.. et si vous l'avez simulé, vous devez l'avoir compris. Sinon, quel modèle mathématique avez-vous écrit ?

une simulation n'est pas un modèle mathématique. C'est une simulation. J'ai fait des trajectoires paraboliques, que se passe-t-il avec des trajectoires circulaires ? et elliptique ? un modèle mathématique répond à cette question, une simulation non.

Ce n'est pas intuitif de toute façon. le plan incliné ne présente pas un "angle inférieur". l'angle moyen est le même, sinon il ne viendra pas au même point. aussi dans un domaine conservateur ce que vous dites est très contre-intuitif, rien d'autre!

peut-être la variable non considérée est l'énergie cinétique stockée par la sphère sous le signe de la rotation autour de son axe baricentrique.

Ma simulation considère un point matériel. Vous avez raison, mais le phénomène est observé de la même façon.

 

[cacciatorino]

Ma simulation considère un point matériel. Vous avez raison, mais le phénomène est observé de la même façon.

considérer qu'à la fin du plan vous avez que l'énergie potentielle initiale est égale à l'énergie cinétique finale, énergie cinétique qui est la somme de cette linéaire et celle de la rotation. Votre logiciel nécessite-t-il le diamètre de la boule comme paramètre, ou considérez-vous l'objet point?

 

[mamobono]

"Si le plan est clair, je vais prendre du temps. Si la surface est courbée, je la mettrai ? Plus ? Moins ? "
à ces questions la réponse est:
la propriété de la brachistochrine cycloide
... Johann bernoulli a proposé un défi à tous les mathématiciens européens, y compris les suivants
problème: sont donnés deux points dans un plan vertical a et b, avec plus de b, mais pas sur
verticale de b, et un fil de fer mince sur lequel une perles peut couler sans friction. trouver quelle forme donner au fil de fer pour que la perle utilise le moins de temps possible pour passer de à b sous l'action de la gravité.
en d'autres termes, la forme à donner au fil de fer correspond à la trajectoire que doit suivre le corps (à ce lien sans friction) pour employer le moins de temps entre a et b sous l'action du
la gravité. à cette trajectoire nous donnons le nom de brachistocrone. . voir le pdf

alors si nous considérons la friction en faisant le budget énergétique, nous pouvons évaluer la vitesse de sortie dans les cas droit et cycloid

mais je ne me débarrasse pas de + je suis trop vieux et rouillé

Bonjour.

 

[Fulvio Romano]

considérer qu'à la fin du plan vous avez que l'énergie potentielle initiale est égale à l'énergie cinétique finale, énergie cinétique qui est la somme de cette linéaire et celle de la rotation. Votre logiciel nécessite-t-il le diamètre de la boule comme paramètre, ou considérez-vous l'objet point?

Je l'ai écrit, c'est un point important. Des points.

... Johann bernoulli a proposé un défi à tous les mathématiciens européens, y compris les suivants
problème:

Tu as pris ma journée. Donc je ne suis pas le con, c'est le problème qui est complexe.

Frappe !

 

[Fulvio Romano]

Je lis des pdf avec passion. C'est magnifique.

et démontre d'ailleurs une des définitions de l'ingénieur comme "celui qui a oublié plus de mathématiques que vous n'avez jamais connu"

 

[Stan9411]

une simulation n'est pas un modèle mathématique. C'est une simulation. J'ai fait des trajectoires paraboliques, que se passe-t-il avec des trajectoires circulaires ? et elliptique ? un modèle mathématique répond à cette question, une simulation non.

Désolé, mais comment avez-vous obtenu les cartes de position, la vitesse et l'accélération pour différentes pistes si vous n'avez pas écrit le modèle mathématique?

Ce n'est pas intuitif de toute façon. le plan incliné ne présente pas un "angle inférieur". l'angle moyen est le même, sinon il ne viendra pas au même point

mais l'allégation que la balle reçoit va avec la petite chose de l'angle d'inclinaison ... si vous lui donnez un plan presque vertical tout au long de la première partie de la trajectoire change tout le profil de vitesse ... que l'angle moyen est le même n'a rien à voir avec elle. Je pense que vous avez quitté la trajectoire et vous êtes retourné à la vitesse et à l'accélération, mais ce n'est pas vrai. est un système d'accélération (variable) imposé.

Si je peux, ce soir, j'essaie d'écrire en matlab les équations qui, à mon avis, régissent ce phénomène.

Je suis désolé d'avoir été pris comme un gars qui écrit des conneries... Peut-être que je te le dis vraiment... quand j'ai un moment j'essaie de me soutenir moi-même avec des chiffres.

 

[Fulvio Romano]

Désolé, mais comment avez-vous obtenu les cartes de position, la vitesse et l'accélération pour différentes pistes si vous n'avez pas écrit le modèle mathématique?

le modèle mathématique est une formule, une équation, une fonctionnelle qui décrit le phénomène. une simulation est faite au moyen d'un processus itératif qui calcule pour chaque instant la valeur de la prochaine habitation. à la fin de la simulation vous n'avez pas le modèle mathématique du phénomène, mais seulement sa représentation graphique dans les conditions dans lesquelles la simulation a été lancée.

mais l'allégation que la balle reçoit va avec la petite chose de l'angle d'inclinaison ... si vous lui donnez un plan presque vertical pour toute la première partie de la trajectoire change tout le profil de la vitesse

Regarde mes cartes. De toute évidence, cela change le profil de vitesse.