Mello Dessi
Guest
Salut, je suis nouveau, et je voudrais remercier ceux qui me répondront.
Ma question est la suivante :
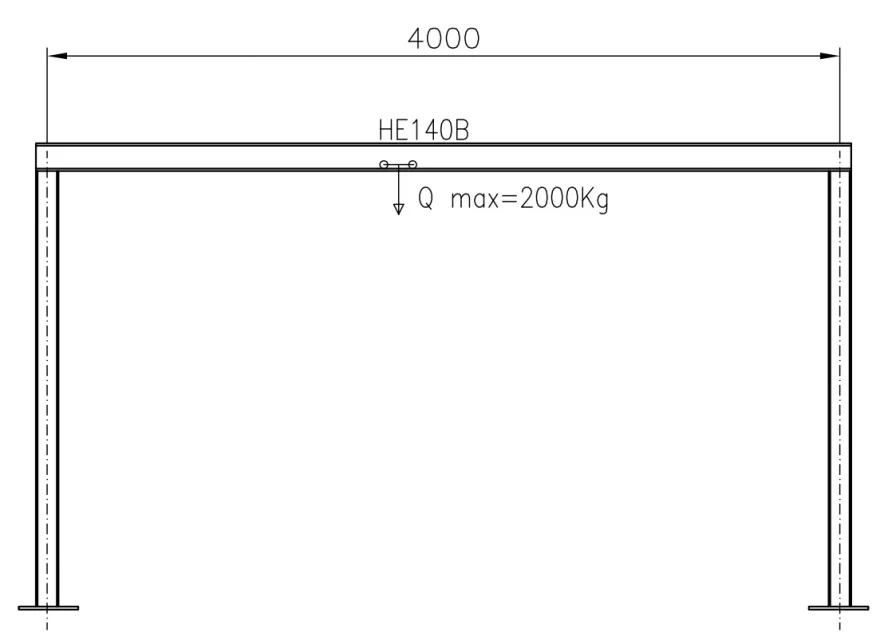
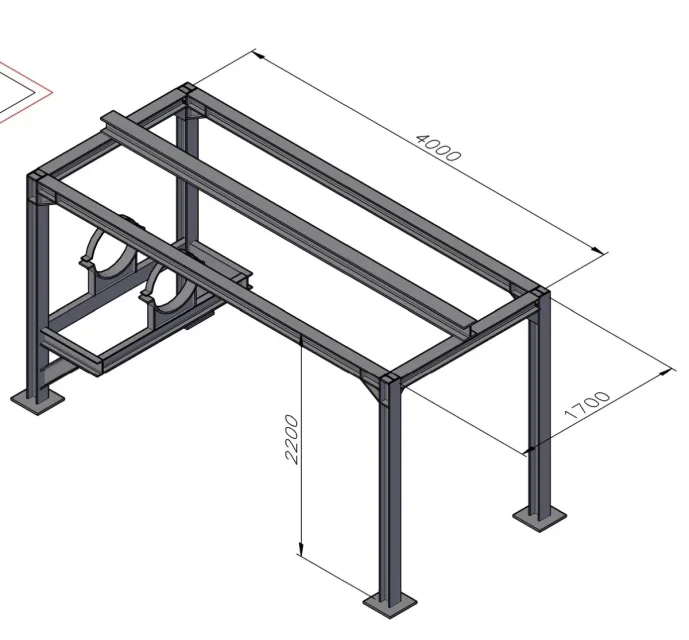
Je dois vérifier la portée d'un matériau de poutre heb140 s235, les 2 supports sont soudés à une distance de 4mt, sur 2 installations.
ce palan avec roues, il doit être monté et coule sur l'aile inférieure de l'héb140.
le palan a une capacité de 2 tonnes.
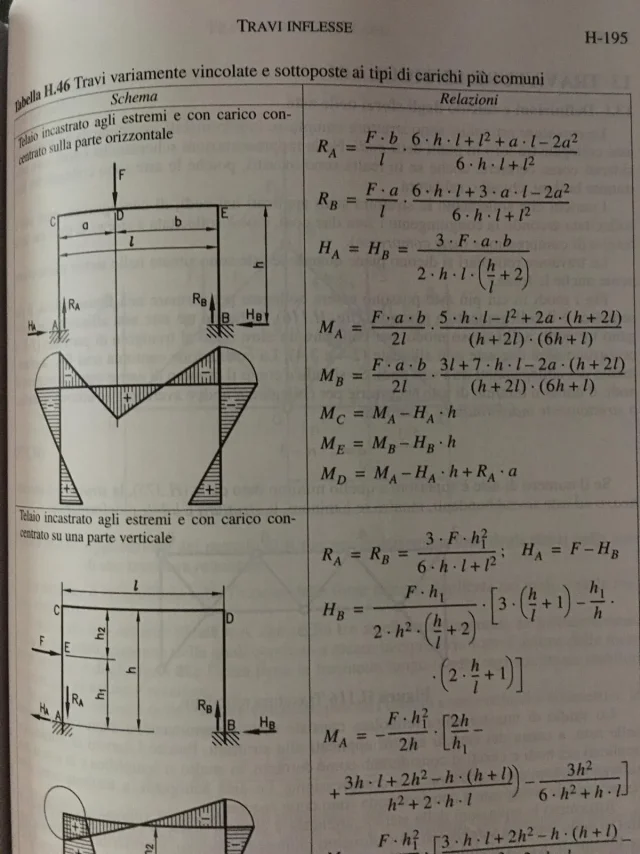
Je voulais savoir si vous deviez calculer la taille de l'aile seule (comment?) ou simplement calculer la poutre de la manière classique de "trave doublement coincé avec la charge concentrée"? - Oui.
pour mieux comprendre, j'attache la photo:
Merci d'avance.
salutations
Ma question est la suivante :
Je dois vérifier la portée d'un matériau de poutre heb140 s235, les 2 supports sont soudés à une distance de 4mt, sur 2 installations.
ce palan avec roues, il doit être monté et coule sur l'aile inférieure de l'héb140.
le palan a une capacité de 2 tonnes.
Je voulais savoir si vous deviez calculer la taille de l'aile seule (comment?) ou simplement calculer la poutre de la manière classique de "trave doublement coincé avec la charge concentrée"? - Oui.
pour mieux comprendre, j'attache la photo:
Merci d'avance.
salutations