انضم إلى منتدى المصممين
خبرتك ضرورية للمجتمع. انضم إلينا وساهم بمعرفتك
انضم إلى المنتدى الآنشارك وتعلّم وتقدّم مع أفضل المحترفين في هذا المجال
مفارقة المكثفين هي تجربة فكرية استفزازية تم إعدادها لكشف بعض القيود المفروضة على نمذجة الدوائر الكهربائية، وقد تم ابتكار العديد من الطرق المختلفة لحل المفارقة. سأضيف حلاً للمزيج الذي يمكن تصميمه في COMSOL Multiphysics® ثم نتوسع فيه لطرح سؤال أكثر استفزازًا والإجابة عليه: هل توجد السعة والتحريض؟ دعونا الغوص في!
مفارقة المكثفين
عادةً ما يتم تقديم هذه التجربة الفكرية على النحو التالي: لنفترض جهازًا يتكون من مكثفين متكافئين، بسعة، ج، متصلين بالتوازي مع وجود مفتاح مفتوح بينهما. جميع الأسلاك والمكثفات مصنوعة من مواد مثالية خالية من المقاومة ولا تفقد. أحد المكثفات مشحون بجهد كهربائي السادس، وبالتالي فإن الشحنة المخزنة هي س = CV_i. لا يوجد فرق جهد على المكثف الآخر، لذلك لا يحتوي على شحنة مخزنة. ماذا يحدث عند إغلاق المفتاح؟

رسم تخطيطي لمفارقة المكثفين. مكثف واحد لديه فرق محتمل بين اللوحات. ماذا يحدث عند إغلاق المفتاح؟
بعض العروض التقديمية لهذه التجربة الفكرية ستلقي ذريعة وتدعي أن الشحنة الموجودة في المكثف الأول سوف تتدفق إلى المكثف الثاني، مما يقلل فرق الجهد في الأول ويزيده في الثاني حتى يتم الوصول إلى حالة مستقرة – عند هذه النقطة فرق الجهد هو نفسه في كل من المكثفات ونصف السادس، منذ نفس التهمة، س، منتشر الآن عبر مكثفين مكافئين. ومع ذلك، يؤدي هذا على الفور إلى مفارقة، لأن الطاقة الموجودة في كل مكثف W_C = \frac{1}{2} C \Delta V^2. إذا كانت الطاقة الأولية \frac{1}{2} C V_i^2 والطاقة النهائية هي 2 \frac{1}{2} C\left( V_i/2 \right)^2 = \frac{1}{4} C V_i^2أين ذهب النصف الآخر من الطاقة؟
هناك العديد من الحلول المتاحة التي تستدعي كل شيء بدءًا من ميكانيكا الكم وحتى الديناميكا الحرارية. من المحتمل أن تكون جميع هذه الحلول صالحة من وجهة نظر تعليمية. ومع ذلك، فإن العديد منهم يلجأون ضمنيًا إلى الواقع بالقول إن الأسلاك والمكثفات يجب أن تتمتع ببساطة ببعض المقاومة أو يجب أن يكون لها بعض الحث. لكن لماذا؟ على الأقل في سياق التجربة الفكرية، قد يكون من المعقول افتراض وجود مواد غير قابلة للضياع تمامًا، وبالتالي إهمال المقاومة. ولكن ماذا عن الحث؟ في سياق هذه التجربة الفكرية، هل يمكننا إهمال الحث؟ دعونا نتبع هذا السؤال ونرى ما إذا كان يقدم إجابة مثيرة للاهتمام …
حل بسيط للمفارقة
يتكون جهازنا من مكثفين مثاليين بدون فقدان. لكن حتى المكثف المثالي يجب أن يفصل شحناته مكانيًا. وهذا يعني أن المكثف يجب أن يكون له حجم معين. وإذا كان لكل مكثف حجم، فلا بد من فصله بمسافة غير صفرية عن المكثف الآخر. لذا، إذا أعدنا رسم المخطط قليلًا، فسنرى أن لدينا مكثفين وحلقتين نصفيتين بقطر محدود من سلك عديم الضياع، يمكن أن يتدفق عبرهما تيار متغير بمرور الوقت. ولكن ماذا نسمي مثل هذا الهيكل؟ مغو!
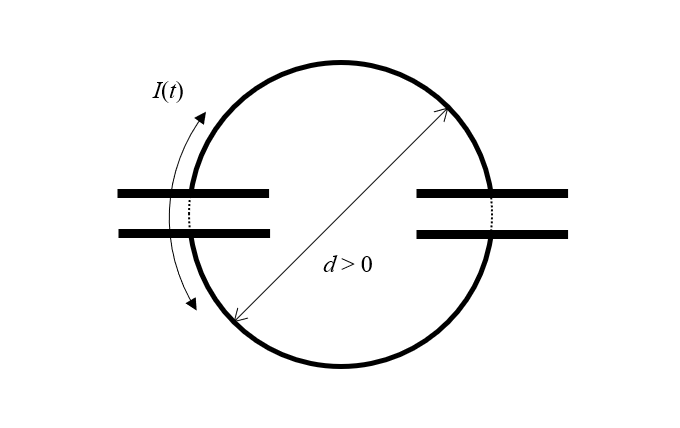
يمكن حل المفارقة من خلال إدراك أن البنية يجب أن يكون حجمها غير صفري، مع تدفق تيار حول حلقة ذات مساحة محدودة، وبالتالي فهي أيضًا مغوِّية.
يجب أن يكون للبنية التي رسمناها هنا حجم محدود، وبالتالي يجب أن يكون لها أيضًا محاثة، طالما أنها موجودة داخل كوننا، حيث يتمتع الفضاء الحر بنفاذية مغناطيسية. إذن ببساطة، نتيجة لوجود مكثف في الدائرة، لا بد أن يكون هناك أيضًا ملف حث في الدائرة. في الواقع، يصبح الأمر أفضل: إذا كان لدينا ملف حث، حتى لو كان بدون فقدان، فإن أي تيار متغير بمرور الوقت يتدفق عبره سيؤدي إلى مجال كهربائي موجود بين لفات المحرِّض، وبالتالي أي ملف حث نضيفه إلى هذا تعمل الدائرة أيضًا كمكثف! يمكننا أن نتبع هذا التسلسل المنطقي إلى ما لا نهاية، ولكن لأغراضنا يكفي مجرد تعديل دائرتنا باستخدام ملف حث واحد له محاثة، ل.
لدينا الآن إل سي الدائرة، ولها حل تحليلي يزيل المفارقة على الفور: سوف يتدفق التيار ذهابًا وإيابًا بين المكثفات وعلى طول الأسلاك ذات الطول المحدود، ويتأرجح عند تردد محدد بواسطة: f=1/\sqrt{2\pi LC}. لن يكون هناك أبدًا حل للحالة المستقرة، لذلك لا يمكننا أبدًا تقييم الطاقة الكهروستاتيكية وحدها. علينا أيضًا أن نأخذ في الاعتبار الطاقة الناتجة عن الشحنات المتحركة، أي تدفق التيار، أنا، وهذا يعطى من خلال: W_L = \frac{1}{2} LI^2. مجموع هذه الطاقة الكهربائية والمغناطيسية (\frac{1}{2} LI^2 + \frac{1}{2} CV^2) لن يتغير مع مرور الوقت.
التحقق في COMSOL Multiphysics® برمجة
من السهل إنشاء نموذج يتحقق من هذا الموقف باستخدام COMSOL Multiphysics® ووحدة الترددات اللاسلكية. سنفعل ذلك باستخدام الموجات الكهرومغناطيسية، العابرة واجهة جنبا إلى جنب مع الكهرباء الساكنة واجهة لحساب الشروط الأولية. سنقوم بتصميم منطقة صغيرة من الفراغ المثالي مع وجود المكثفات والأسلاك بداخلها. يتم التعامل مع ألواح المكثفات والأسلاك والمساحة المحيطة بالحجم على أنها موصلات كهربائية مثالية، مما يعني أن المجالات الكهرومغناطيسية لن تخترق أي حدود. يوجد دليل لإعداد نماذج التفريغ السعوي في مقالة مركز التعلم لدينا: “نمذجة التفريغ السعوي”.
حل نموذج المجال الزمني هذا وتقييم إجمالي الطاقة الكهربائية والمغناطيسية يوضح السلوك التذبذبي المتوقع. من الممكن أيضًا تقسيم مجال النمذجة إلى مناطق مختلفة لتقييم إجمالي الطاقة في المناطق المحيطة بالمكثفين وكذلك في الفضاء المحيط. توضح هذه المؤامرة كيف تتأرجح الطاقة في المكان والزمان.
رسم متحرك يوضح التيارات الموجودة على سطح ألواح وأسلاك المكثف بالإضافة إلى المجال المغناطيسي الموجود بينهما.
يتأرجح إجمالي الطاقة الكهربائية والمغناطيسية مع مرور الوقت؛ لا يتغير المجموع في هذا الجهاز الخالي من الضياع.
يظهر مجموع الطاقة الكهربائية والمغناطيسية في المجالات المختلفة أن الطاقة تتأرجح في الزمان والمكان.
يمكننا أن نلاحظ أن هذه المؤامرات ليست جيبية تمامًا من حيث الزمن، ويجب أن نتساءل عن سبب ذلك. من أين يأتي هذا المحتوى عالي التردد، أي التموجات في الطاقة بمرور الوقت؟ أنها تنشأ من الهيكل. من الواضح تمامًا أن اللوحتين لهما سعة محددة جيدًا، ولكن هناك أيضًا فصل للشحنات بسبب الأسلاك، وكل هذا الهيكل يقع داخل تجويف أسطواني له تردد رنين. كل هذه الأجزاء المختلفة من الجهاز لها بعض المساهمة في السلوك الكهرومغناطيسي. قد تكون كل مساهمة صغيرة جدًا، ولكنها موجودة دائمًا عندما ننظر إلى هيكل محدود الحجم.
طرح المزيد من الأسئلة: هل توجد سعة ومحاثة؟
لقد حان الوقت الآن لطرح سؤال أكثر استفزازًا حول هذا الجهاز الكهرومغناطيسي (أو أي جهاز آخر): هل لديه سعة أم محاثة؟ لقد رأينا بوضوح أن هذا الجهاز بالذات يحتوي على كليهما. ولكن ماذا لو قمنا بتعديله بإضافة مادة عازلة قوية جداً بين ألواح المكثف؟ وهذا من شأنه أن يجعل السعة أكبر بكثير لكنه يترك الحث دون تغيير. وإذا جعلنا السعة أكبر بكثير، فهل يمكننا القول أن التحريض لا يهم؟
باختصار: لا، لا ينبغي لنا أبدًا أن نفكر في الجهاز الكهروديناميكي باعتباره سعويًا بحتًا أو حثيًا بحتًا. في الأجهزة الكهروديناميكية، ستكون هناك دائمًا طاقة كهربائية بسبب الفصل المكاني للشحنات وطاقة مغناطيسية بسبب حركة الشحنات. على الرغم من أنه يمكننا في بعض الأحيان بناء مواقف افتراضية حيث يمكن تجاهل أحدهما أو الآخر، إلا أنه يتعين علينا دائمًا أن نتذكر أننا نقوم بتبسيط عقلي.
علاوة على ذلك، تتمتع جميع المواد الحقيقية أيضًا ببعض المقاومة المحدودة، لذا، لكي نكون أكثر واقعية، يجب أن نتحدث عن كل شيء على أنه يحتوي على ممانعة – وهذا هو المكان الذي نضع أنفسنا فيه في بعض الأحيان في المزيد من المشاكل. عند التعامل مع نموذج مجال التردد، يوجد تعبير مألوف جدًا لممانعة جهاز كهربائي:
Z = R + j\omega L -j\frac{1}{\omega C}
المقاومة، ر، في هذا التعبير مقياس لكيفية تحويل الطاقة الحركية للشحنات المتحركة، أي التيار، إلى طاقة حرارية.
يمكن التعرف على هذه المعادلة على الفور على أنها تتعلق بمذبذب توافقي مخمد بدرجة واحدة من الحرية، وهي واحدة من أكثر المشاكل المدروسة جيدًا في الهندسة والفيزياء. نحن نعلم أنه يمكننا أن نحسب من هذا التعبير تردد الرنين وعامل الجودة لمثل هذا المذبذب، ونعلم أن الأجهزة الحقيقية لها عامل رنين وجودة أساسي. وهذا يغرينا بمساواة الاثنين ومحاولة اختزال جهاز كهربائي محدود الحجم في العالم الحقيقي إلى مقاومة وسعة ومحاثة واحدة. يعد هذا خطأً مفاهيميًا وغير صالح أبدًا لأن التعبير أعلاه للممانعة ينطبق فقط على الجهاز الذي له حجم متناهٍ في الصغر.
أي جهاز حقيقي له حجم محدود، وعندما يعمل بالرنين فإن الطاقة الكهربائية والمغناطيسية تختلف في المكان والزمان، كما رأينا من المخططات أعلاه. لذلك، يتطلب نموذج الدائرة المكافئة ثلاث عقد على الأقل (ثلاث عقد على الأقل)، على الرغم من أنه في بعض الأحيان أكثر من ذلك بكثير. بالعودة بأفكارنا مرة أخرى إلى نموذجنا الفيزيائي للمكثفين وافتراض أن لوحة كل مكثف ممثلة بعقدة في الدائرة الكهربائية، يمكننا أن نرى أن نموذج الدائرة المكافئة يجب أن يكون على الأقل معقدًا مثل الدائرة الموضحة أدناه، مع أربع العقد. لاحظ أنه تمت إضافة سعة صغيرة بالتوازي مع محاثة الأسلاك نظرًا لوجود فصل للشحنات على طول الأسلاك أيضًا.
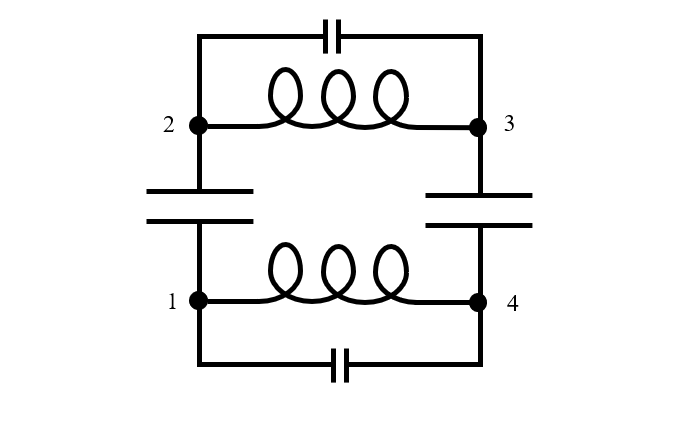
نموذج دائرة مكافئة مكونة من مكثفين محدودي الحجم عديمي الضياع متصلين على التوالي.
نأمل أن نرى من هذا المثال أن بناء نموذج دائرة مكافئ صالح بالقرب من الرنين يمكن أن يصبح سريعًا أمرًا معقدًا للغاية، ويتطلب رؤية فيزيائية، وقليلًا من الخبرة مع الأجهزة المماثلة، والنمذجة الرقمية.
وبالعودة إلى السؤال الأصلي، يمكن القول بأن السعة، والتحريض، وحتى المقاومة هي مفاهيم لا توجد بمفردها، بل إنها موجودة فقط مع بعضها البعض. على الرغم من أننا نستطيع في بعض الأحيان تقليل ممانعة الجهاز المعتمدة على التردد وصولاً إلى مقاومة و/أو سعة و/أو محاثة واحدة، إلا أن مثل هذه التبسيطات صالحة فقط عند الترددات الأقل من رنين الجهاز. إن وضع ذلك في الاعتبار يساعدنا على تجنب جميع أنواع المزالق، بدءًا من مفارقة المكثفين المسلية هذه إلى مشاكل العالم الحقيقي الأكثر إحباطًا.
الملاحظات الختامية
لقد استخدمنا هنا تجربة فكرية كلاسيكية لفهم لماذا لا يمكن تحليل ممانعة جهاز كهرومغناطيسي يعمل بالقرب من الرنين إلى مقاومة واحدة مكافئة، وهي السعة والمحاثة. تعتبر التجارب الفكرية مثل مفارقة المكثفين ذات قيمة لتوسيع فهمنا للكهرومغناطيسية وتفسير نتائج نماذجنا الحسابية.
قراءة متعمقة
هل أنت مهتم بمعرفة كيفية استخدام النمذجة والمحاكاة لحل الألغاز الذهنية الأخرى؟ تحقق من بعض الأمثلة الأخرى على مدونة COMSOL:
انضم إلى منتدى المصممين
خبرتك ضرورية للمجتمع. انضم إلينا وساهم بمعرفتك
انضم إلى المنتدى الآنشارك وتعلّم وتقدّم مع أفضل المحترفين في هذا المجال


