在流程编辑器中可用作适配器驱动程序的技术非常棒。 它们是数值方法深入研究的结果。 最突出的技术是 DOE、优化、近似、六西格码。 我们在之前的博客中详细讨论了 DOE。 在这篇博客中,我们将深入探讨优化。 我们不要忘记,我们是在进行流程设计,因此优化是参数化的,主要由几何或物理参数驱动。
经典优化定义
你在围栏场地的某个地方有一个球。 你有一个起点。 您需要在不越过栅栏的情况下移动最短距离来找到球。 您有传感器可以提供帮助。 球是目标函数。 栅栏是限制。 传感器是所使用的优化技术。

实验设计和优化之间的区别
两者之间的区别就像“更好”和“最好”之间的区别一样。 实验设计是一种以有效的方式从现有点集中挑选最合适的设计点的方法。 该集合可以由用户定义,也可以由 DOE 本身定义。 优化技术从单个初始设计点开始,并在设计空间中迭代导航以达到最优或最佳设计点。 根据问题的不同,DOE 可以成为优化的先驱。
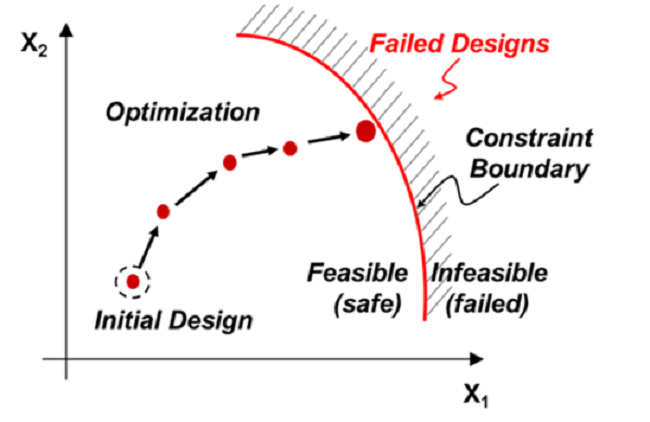
优化技术的类型
根据目标函数的定义方式和合适的设计空间的类型,有不同的方法对它们进行分类。
受限技术: 他们使用单独的功能来操作,一个用于目标,另一个用于约束。 我们都在工程课程中在某种程度上见过这种技术。 它们是最常见的。
在 x1>x>x2 中最小化/最大化 F(x)
满足:h(x)>a1; g(x)>a2; f(x)=0 等
无约束技术: 他们仅使用一种函数来实现目标和约束。 用户仍然定义与目标分开的约束,但在内部受约束的问题被转换为无约束的问题。
根据不同类型的设计空间的应用,优化方法可以分为基于梯度的、直接的或探索性的。 下图中显示的缩写是各个类别中方法的名称。
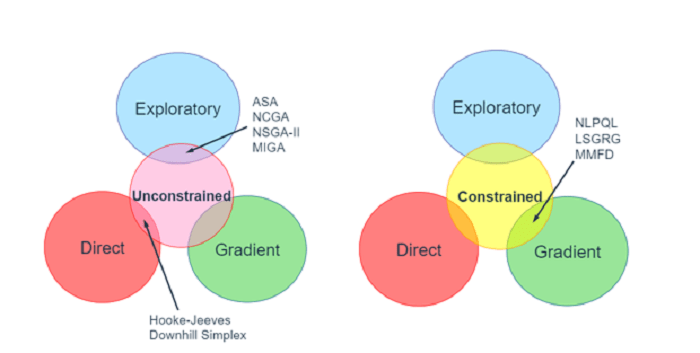
梯度法: 它们是最古老的,并且在行业中经过了充分的测试。 它们的工作原理是最小能量或最大稳定性。 你轻轻地将一个球扔进山谷,它会沿着最陡峭的下降路径滑动,直到到达附近的最低点。 这些方法在具有 C0 和 C1 连续性的连续设计空间中工作。 它们可能会陷入局部最小值,因此应仔细选择初始点。

直接方法: 直接搜索算法从基点开始。 它搜索周围的一组点,寻找目标函数值低于当前点的点。 该算法跳转到该点作为新的基点,并在其周围搜索一组新的点。 人们可以发现这种方法计算效率很高,因为不需要梯度计算。 它更加通用,因为不需要 C0 和 C1 连续性。 最常见的是胡克吉夫斯和下坡单纯形。
胡克吉夫斯方法跟踪其行进方向。 如果行进方向上存在较低点,则它不会每一步都改变方向。

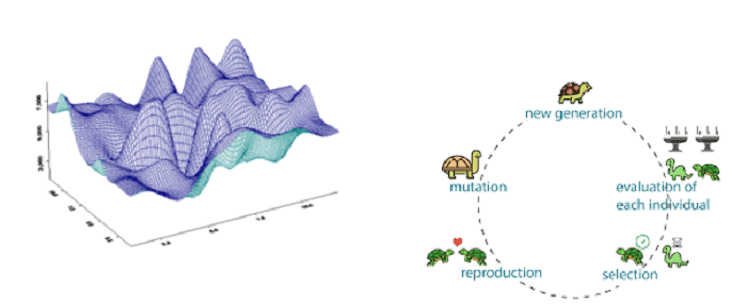
探索性方法:这些方法基于称为父项的一个点数据集之间的交叉或变异技术,以生成称为子项的另一点数据集。 新的数据集随着每次突变而演变,并且越来越接近最优解。 这是一种高保真度方案,适用于各种目标函数:不连续、不可微、随机、混合整数类型以及具有多个峰和谷的高度非线性,如下所示。 然而,就计算费用而言,它是最昂贵的优化方案。 最常见的方法是遗传算法、粒子群算法和自适应模拟退火。
基于指针的方法:这是一种混合搭配方法,以防用户不知道哪种类型的技术最适合以合理的精度解决问题。 当用户遇到不熟悉且难以可视化的设计空间类型时,指针方法可能会有所帮助。 指针方法可以利用最多三种优化方案,最好是每个篮子中一种:梯度、直接和探索性。 随着优化的进行,算法会跟踪每种方法的功效并使用最适合给定问题的方法。

