概括
使用多体动力学 (MBD) 时,建立一个不需要太长时间求解的模型非常重要。 使用刚体是实现这一目标的最佳方法。 在 Ansys Motion 中,当需要一些柔性零件时,有两种方法可以计算主体中的应力:节点方法(利用完整的有限元公式)和模态方法(采用模态线性展开)。 本博客对这两种方法进行了比较,以确定压力结果的差异。
模态和节点分析。
使用节点方法,求解器将执行完整的 FEA 计算,涉及模型内的最大自由度 (DOF) 和矩阵大小。 另一方面,模态方法假设变形向量 你 通过线性组合一组振型来表示。
![]()
比例因子或幅度 A 称为模态坐标, Ψ 是一组振型。
我们可以看到变形可以构建为:

然后,求解器将首先计算柔性零件的模态分析,并使用计算出的模态来求解模型。 在这种情况下,自由度的数量将大大减少。 该方法仅适用于线性模型。
运动模型。
在此示例中,使用各种关节和运动功能来模拟液压挖掘机组件以复制液压执行器。 将负载施加到铲斗上以模拟其承载的重量。 该模型使用不同的方法进行求解。 最初,使用刚体来建立基本求解时间。 随后,第二个模型涉及使用节点方法的 5 个柔性体。 最后,最后一个模型也利用柔性体,但采用模态解决方案而不是完整的 FEA 节点计算。
对于刚体模型,计算时间不到一秒。 然而,该模型不会产生任何应力或应变结果。

当采用节点方法时,需要超过 47k 个自由度和 271 秒才能获得解决方案。
![]()

使用模态柔性体,分析大约有 200 个自由度,大约需要 5 秒。 这是与完整 FEA 计算的重要区别。
![]()
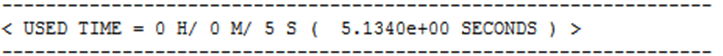
压力结果。
两个模型中不同时间步长期间的等效应力基本相同。 节点模型(右侧)在 6.80 秒时达到的最大值为 112.08MPa,模态模型在 6.72 秒时达到的最大值为 111.96。 应力差为0.107%。
附加说明
您可以控制用于每个实体模态扩展的最大模态数量,并查看如何抑制第一个模态形状以提高解决方案的质量。
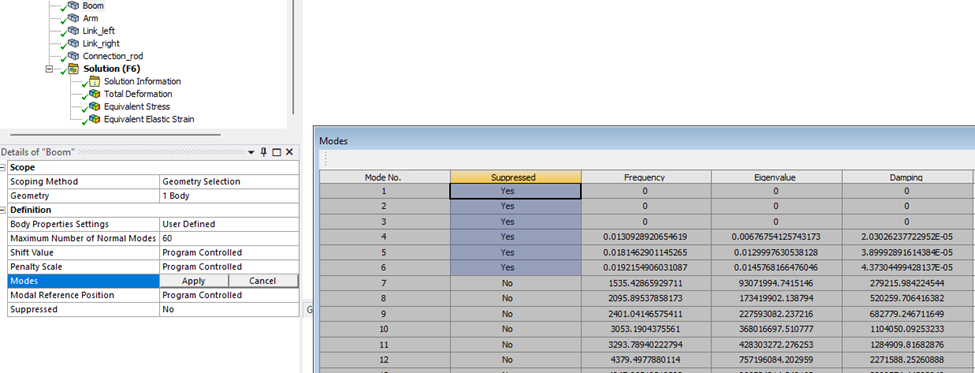
建议
不可能对模态体使用非线性材料。 仅当应用小变形和线性材料假设时才使用此技术,这一点很重要。
结论
模态体方法对于快速找到解决方案和验证一般应力状态非常有用。 一旦确定线性材料是否适用于每种特定情况,用户可以根据需要切换到节点分析。
在初步设计阶段,使用这种方法节省的时间可能至关重要。 用户可以测试各种场景,然后在确定最有希望的场景后过渡到完整的节点模型。

