摘要
在本讨论系列的第一部分中,我探讨并验证了手工计算与物体跌落到刚性表面上的随时间变化的响应之间的关系,以及在冲击期间会发生哪些偏转和应力。 下面讨论的概念对于理解如何使用 ANSYS Mechanical 设置和解决瞬态结构分析至关重要。
图 1:撞击过程中的杆件(挠度比例夸大)。
图 1 展示了我们的示例杆在跌落后的情况,并显示了冲击期间发生的情况。 本文其余部分将探讨如何设置和分析此类系统,并将我们的进展与普通手工计算进行比较。
以下是本讨论涉及的主题列表(按出现顺序排列):
- 势能
- 弹性能
- 方向刚度
- 静态结构分析
- 平均压缩力
- 动能
- 冲击速度
- 撞击周期
- 自然频率
- 模态有效质量
- 瞬态结构分析
- 分析持续时间
- 时间步频
- 复杂瞬态位移和应力结果
- 平均压缩应力
详细信息
我开始探索手工计算与动态事件(如一个物体撞击另一个物体)产生的最大挠度和应力结果之间的关系。 我使用 ANSYS Mechanical 来验证假设,并提供这些动态事件的更多细节。 我对有限元方法充满信心,并期待着与大家分享我的研究成果。
我从一个简单的圆柱形棒材掉落到刚性表面的例子开始探索。 在这种情况下,以及与本讨论相关的所有情况下,我假定材料具有弹性行为,并且所有载荷都不会导致塑性或损坏。 这意味着几何体内部存在能量守恒。
在此过程中,我做出了一系列假设,并进行了有限元分析,以验证或质疑这些假设。 在这个过程中,我提出了更多的问题,进行了更多的分析,得到了更多的答案。 最后,我能够自信地描述这一动态事件的许多方面,我将尽可能简洁地介绍所有这些方面。
让我们从最简单的想法开始。
第一个例子探讨的是圆柱形棒材掉落到坚硬表面的情况。 圆棒直径为 25.4 毫米,长度为 254 毫米,质量密度为 7.85e-06 [kg/mm³]. 这根棒将从距底面 1 米处落下。
图 2:圆柱形棒材
在这种情况下,势能必须等于弹性能。
势能:

弹性能

让我们将下落圆柱体的势能等同于它的弹性能,以了解我们能否准确预测偏转。
让我们假设圆柱体将沿负 Y 方向下落。 因此,第一步将是确定我们的几何体在 Y 方向上的刚度。
对于我们的模型,可以从理论上推导出这一刚度,也可以使用有限元方法,即施加已知载荷并将该载荷除以计算出的 Y 方向挠度。 这将使我们能够将有限元估算结果与理论推导值进行比较,并对我们的方法产生信心。
让我们来推导理论刚度。 对于 Y 轴方向,适用以下公式:

现在,让我们通过两种不同的有限元分析方法来计算几何刚度,以便了解不同类型的载荷所涉及的不同考虑因素。
在这里,我们考虑一个固定的底座,同时在圆柱体的远端施加一个力,使底座上的反作用力与圆柱体顶部的外力大小相等、符号相反。 只要我们的材料属性是线性的,并且不考虑几何非线性(大变形),那么这个压缩载荷的大小并不重要。
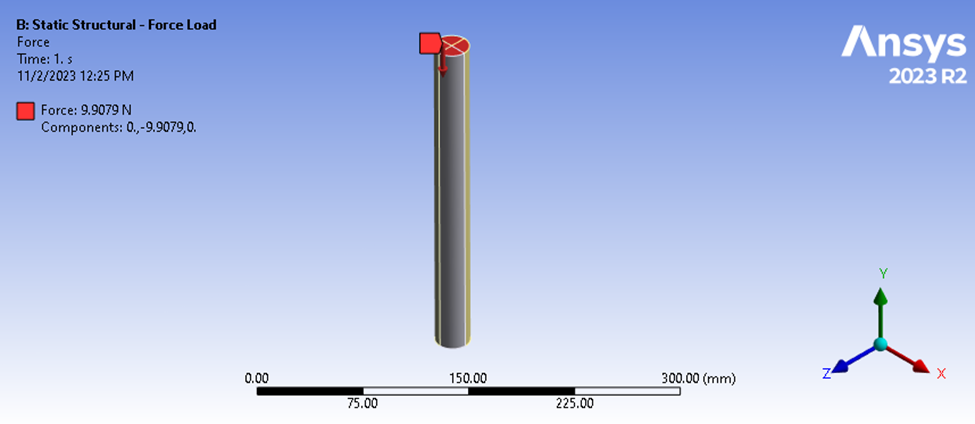
图 3:从顶部加载并在底部支撑的杆的静态结构分析。
在这种情况下,顶部表面承受 9.9079 N 的载荷,而底部表面则固定在 Y 位移上。 该载荷的大小稍后会更清楚。
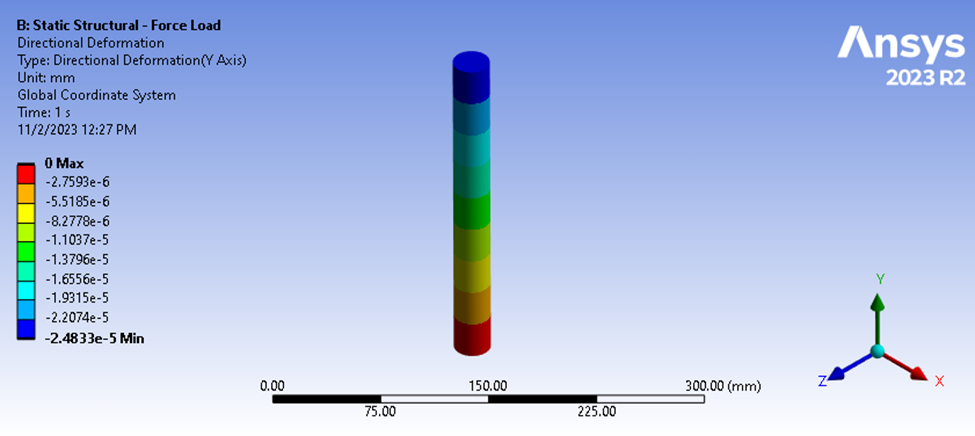
图 4:静态结构挠度结果
静态结构分析的求解结果表明,压缩挠度的最大值为 2.4833e-5 mm。 根据 9.9079 N 的荷载,我们可以计算出以下平均刚度。
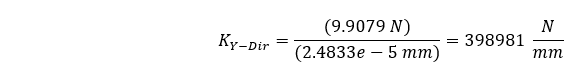
可以看出,有限元方法与理论方法的差异仅为 0.00125%。 这让我们感觉良好 😊
接下来,让我们考虑另一种类型的加载,例如重力加载。 在这种情况下,上表面的力被移除,但下表面仍然受到约束,重力的作用力为 9806.6 毫米/秒^2。 底部的反作用力为 9.9079 牛,但作用在顶面的力绝对为零。 挠度结果显示不同的挠度大小为 1.2421e-5 毫米。
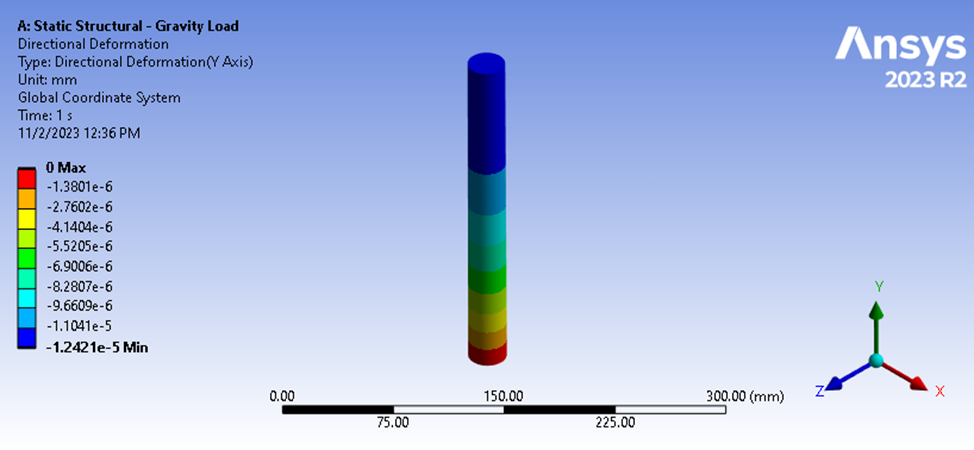
图 5:静态结构分析挠度结果
如果我们试图用上述方程的相同形式来计算刚度,我们会得出错误的值,因为我们没有考虑作用在我们几何体上的平均压缩力。 在这种情况下,我们可以很容易地估算出平均压缩力,因为我们的几何体具有恒定的横截面,而且我们估算出的平均刚度可以计算如下。
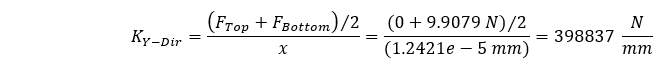
这个估计值与我们的理论计算值相差 0.0348%。 因此,通过两种不同的加载方法,我们可以可靠地估算出几何方向的刚度。
将我们估算的方向刚度与我们的模型和材料特性相结合,我们可以估算出最大挠度如下。
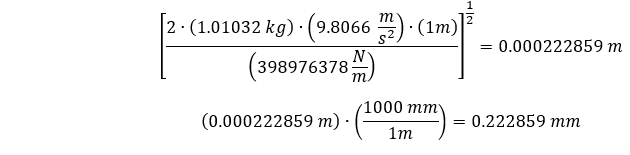
约为 0.223 毫米。 现在,我们需要一个瞬态结构模型来模拟圆柱形钢筋撞击地面时和撞击后的挠度。

图 6:瞬态结构分析模型和约束条件
我们的模型假定棒材以 4428 毫米/秒的速度沿负 Y 方向移动。 我们可以通过将轴的势能等同于撞击瞬间的动能来计算。
动能:
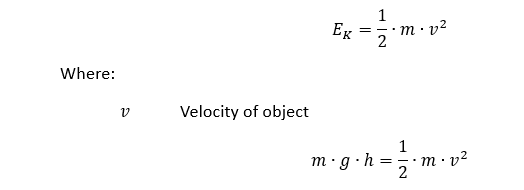
因此

添加约束条件以保持几何体的垂直高度,同时在底座上添加一个仅用于压缩的支撑。 定义分析持续时间(稍后详述)以及用于收集结果的频繁捕获率。
分析结果比较复杂,因为在撞击后横杆顶部向下偏转时,横杆底部可能会由于与纯压缩支撑相关的刚度而受到轻微压缩。 正是这两个表面之间的偏转差值描述了横梁的整体压缩情况。
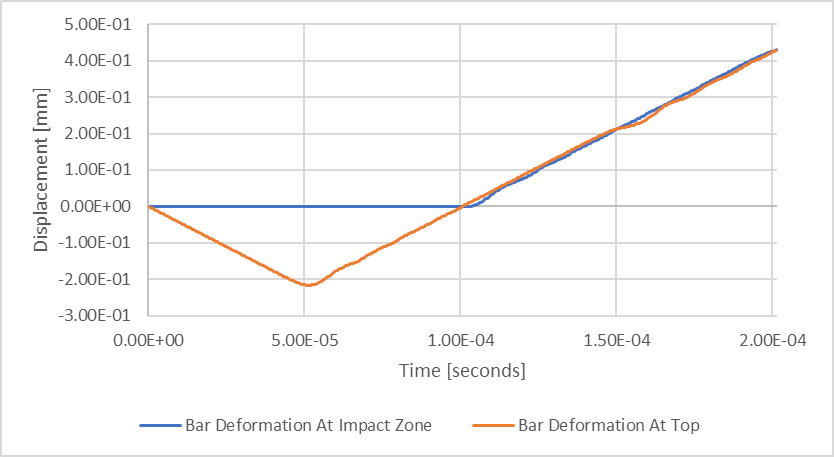
图 7:瞬态结构挠度结果
蓝色线条 “撞击区的杆件变形 “的平缓周期显示了底部发生接触的周期,或者说是与撞击相关的停留时间。 如果我们重新绘制数据,将重点放在这一时期,我们就可以更容易地观察到几个问题。
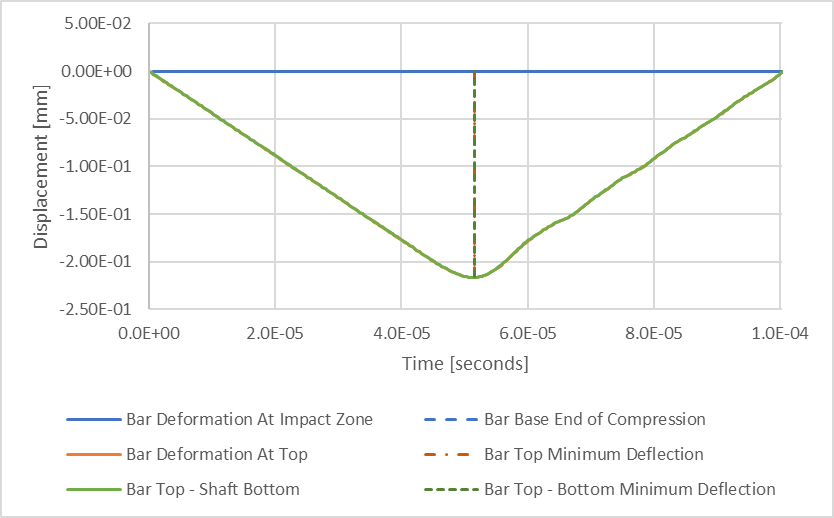
图 8:瞬态结构压缩挠度结果
我添加了一条绿线,表示钢筋顶部和底部表面挠度的差值,从而得出钢筋的总压缩量与时间的函数关系。 两条垂直虚线代表与橙色和绿色线最小结果相关的时间间隔。 我们可以看到,横杆的最小压缩量与横杆顶部的最小压缩量同时出现。 由此,我们可以估计棒材的最大压缩量为 0.216 毫米,比我们估计的最大挠度 0.223 毫米小 3%。
不过,从这个例子及其结果中我们还可以探索和学习到更多。
现在让我们来看看建立瞬态结构分析的方面,特别是与我们的事件相关的时间周期,并确定我们如何为任何几何体估算这个周期。
如果我们看一下蓝线从负位移变为正位移的时间(0.00010026 秒),这相当于与轴压缩相关的周期。
我们的轴可以看作是一个反弹的弹簧。 冲击的持续时间反映了其压缩方向上固有频率周期的 ½。 因此,以下情况应该是正确的。

现在,让我们来探讨是否可以支持这一理论,以及如何估算出这一几何体的固有频率,以及我们希望将来分析的任何几何体的固有频率。
我们可以改变对上述测试模型施加的 “仅压缩 “支撑,在这些相同的表面上施加 Y 方向约束,并在 ANSYS 中直接求解纵向振动频率。
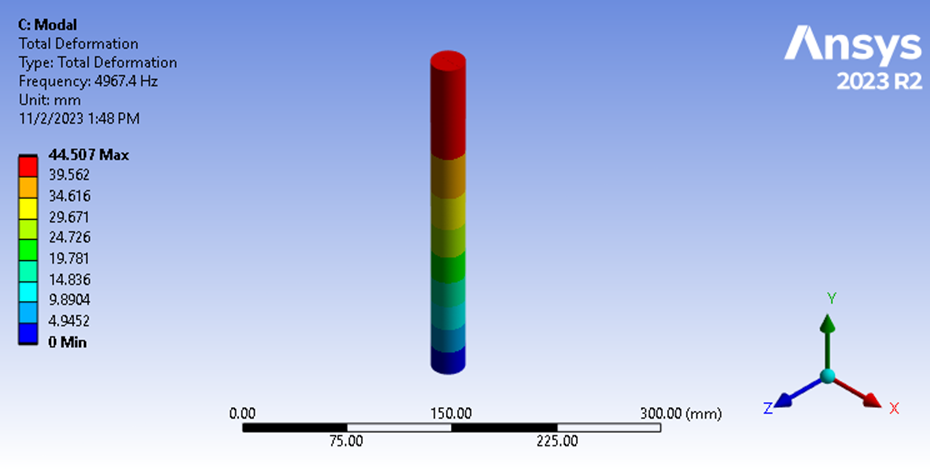
图 9:模态分析基频
这里我们可以看到纵向振动频率为 4967.4 赫兹。 这表明,我们根据瞬态结构位移结果对固有频率的估算精确度在 0.4% 以内。 这一结果证实了我们的理论,即对于两个撞击物体的软体,撞击持续时间等于基频周期的 1/2。
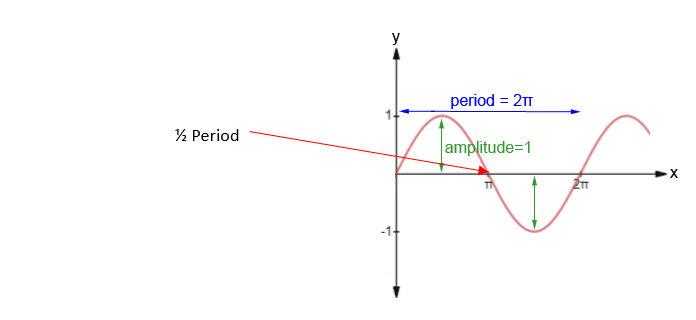
图 10:撞击周期
在我们的分析示例中,我们只有一个部分,并且我们假定只有压缩垂直支撑代表另一个非常坚硬的物体。 因此,我们的轴是这两个冲击伙伴中较为灵活的一个。 我们的瞬态结构分析被定义为分析持续时间等于该固有频率的周期,我们预计撞击发生在该周期的前 1/2。
但是,如果我们要进行瞬态结构分析,该如何计算这个固有频率呢?
我们可以像我刚才演示的那样,对几何体进行模态分析,同时使用约束条件保持冲击姿态,并直接求解冲击压缩的模态振型。 但是否有一种分析方法可以实现同样的目的?
为了探讨这个问题,我们需要计算几何体在冲击方向上的固有频率,计算公式如下。

我们已经探讨了如何估算方向刚度,现在让我们举几个例子来更好地理解模态有效质量。
我们系统的总质量为
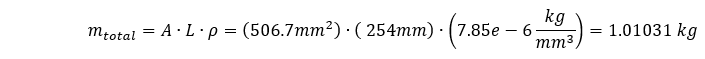
由于几何体的一端受到约束,我们系统的有效质量将小于总质量。 根据几何形状的复杂程度和用于固定几何形状的约束条件,可能很难估算出参与质量的大小。 在我们的案例中,几何形状非常简单,对于一端固定的挤压截面,通常推导出有效质量等于系统总质量的 1/3。 如果是这种情况,那么以下就是我们的基频:
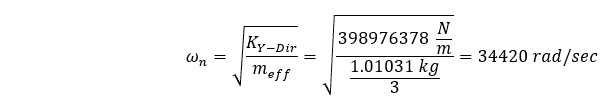
可以更清楚地表述为
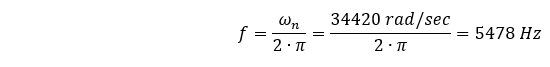
这个值(5478 Hz)比我们用有限元法计算的固有频率(4967.4 Hz)大 10%以上……为什么?
答案与模态有效质量的估算有关。 如果我们对纵向刚度的计算有信心(……我们确实有信心……),那么我们就可以改变模型设置,从而更容易地验证基频的计算结果。
我们将模型材料的质量密度设为零,然后在几何体的远端增加 1.01031 千克的质量,这将产生以下固有频率。
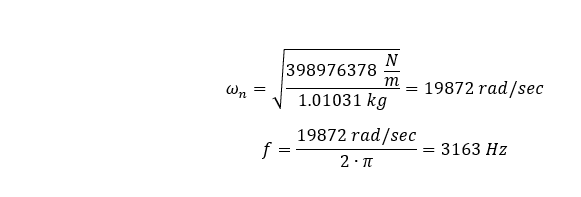
运行有限元分析后,我们可以看到基本纵向频率为 3154.6 赫兹。
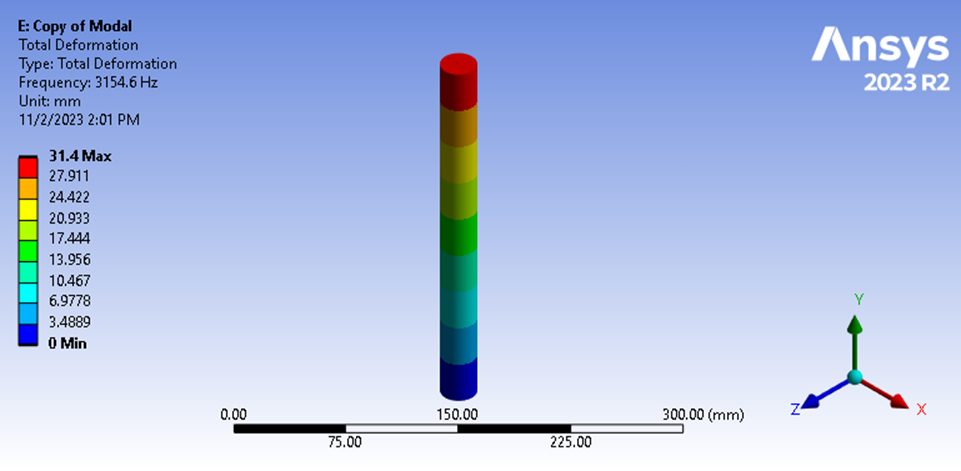
图 11:模态分析基频
这表明与我们的手工计算结果相差 0.27%。 因此,我们对有限元方法有了更多的信心,同时也发现了手工计算中使用的有效质量估算的弱点,即利用整个几何体的分布质量。
通过重新排列方程,我们可以通过考虑 ANSYS 计算的固有频率来求解有效质量,同时考虑分布质量,如下所示:
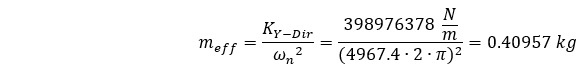
我们发现该有效质量为系统总质量的 0.405。
因此,对于其他更复杂的几何结构,我们可以预期这个质量分数是唯一的,并且具有理论推导的挑战性,我们可以使用有限元方法可靠地求解固有频率。
既然我们已经了解了如何确定给定几何形状的固有频率,我们就需要确定在瞬态分析过程中应在什么频率下收集分析结果。
为此,我们应从两个不同的角度考虑分析步长对分析的影响。 一个角度是对非线性响应(如正弦波)进行片断线性描述时的预期。 另一个角度是实际分析结果如何随捕获率频率的变化而变化。 由于我们考虑的是冲击问题,并且假设冲击周期与挠性组件的基本振动有关,因此有必要探讨步长之间的关系以及步长如何影响正弦曲线的精度。
为了评估这种关系,我们将正弦曲线前半部分的幅度加权平均值与相同跨度的理论平均值进行比较,后者等于:
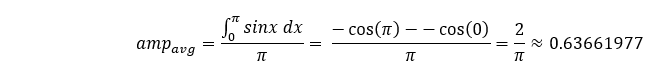
现在,我们通过使用不同的步数来探索如何准确地表示这条正弦曲线,然后使用梯形法则计算前半部分的曲线下面积,再用该面积除以该跨度的周期。
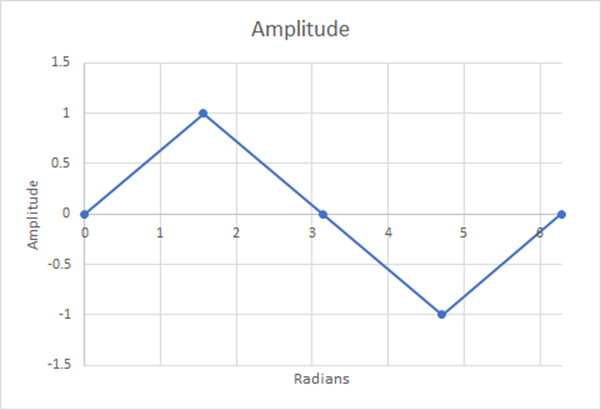
图 12:4 个台阶;估计加权平均值=0.5;21.46% 的差异
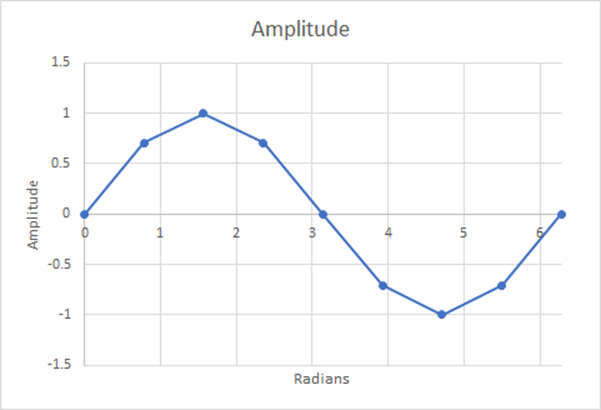
图 13:8 个步骤;估计加权平均值=0.60536;5.19% 差异
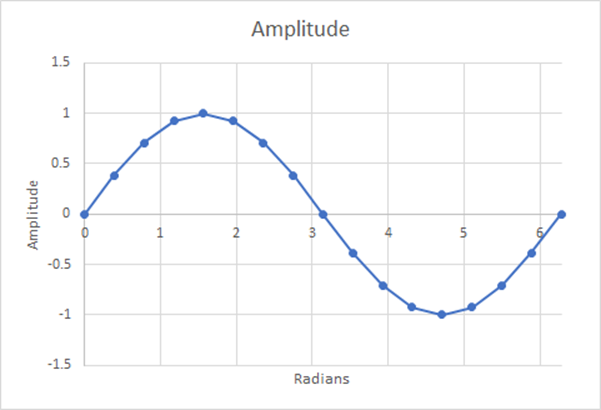
图 14:16 个步骤;估计加权平均值=0.6284;1.29% 差异
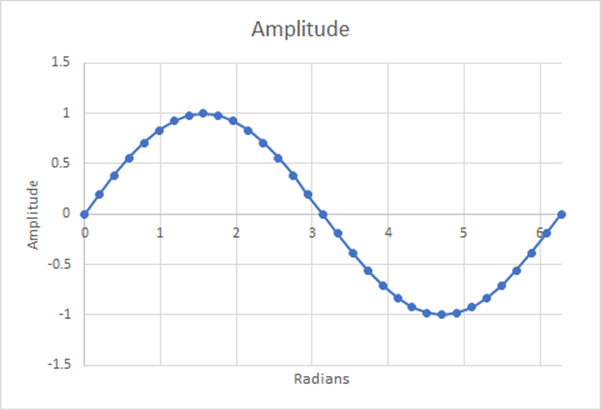
图 15:32 个步骤;估计加权平均值=0.6346;0.32% 差异
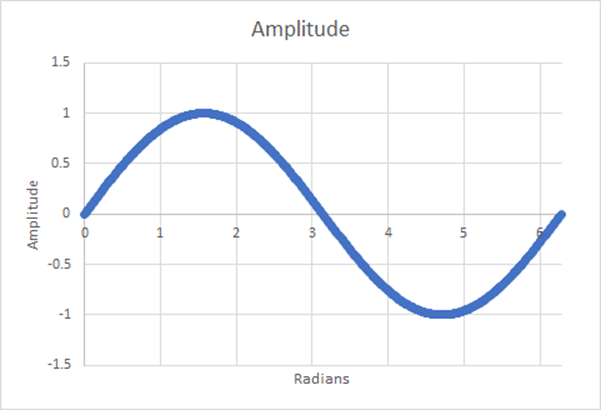
图 16:512 个步骤;估计加权平均值=0.6366;0.001% 差异
事实上,我们从未达到与理论值完全一致的程度,我们可以绘制出随着时间步数的增加,精确度的变化情况,如下图所示。
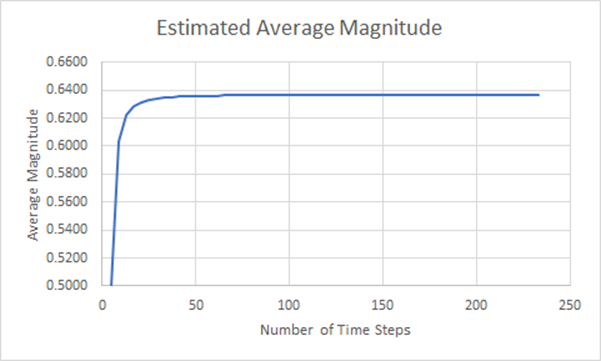
图 17:估计平均振幅收敛图
从图中我们可以看出,随着近似计算步数的增加,精确度也在迅速提高。 但这并没有考虑随着时间步数的增加,结果会如何发展。
为了探讨对分析结果的影响,我们将绘制最大杆压缩结果与时间的函数关系图,同时考虑解法中定义的不同时间步数。
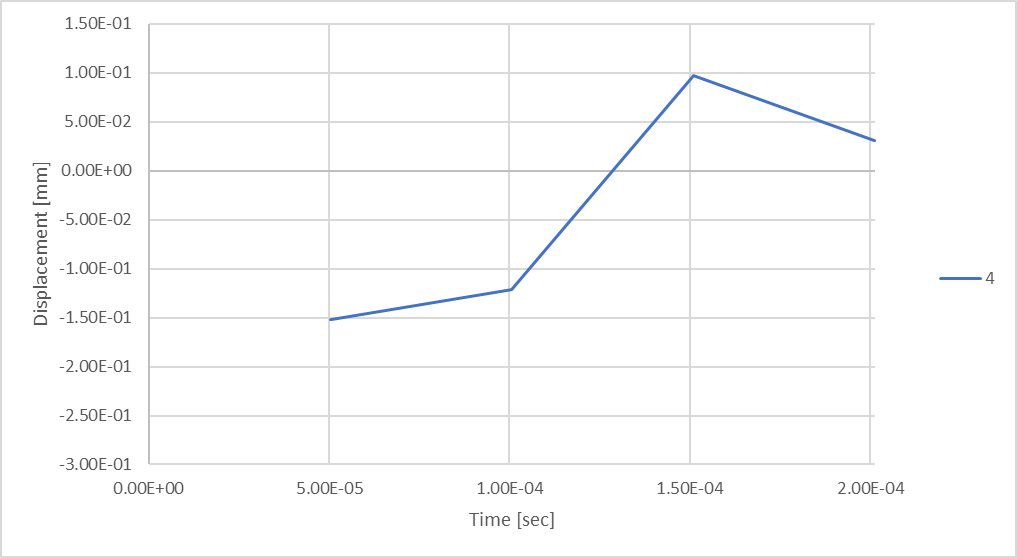
图 18:考虑 4 个时间步长时的杆位移。
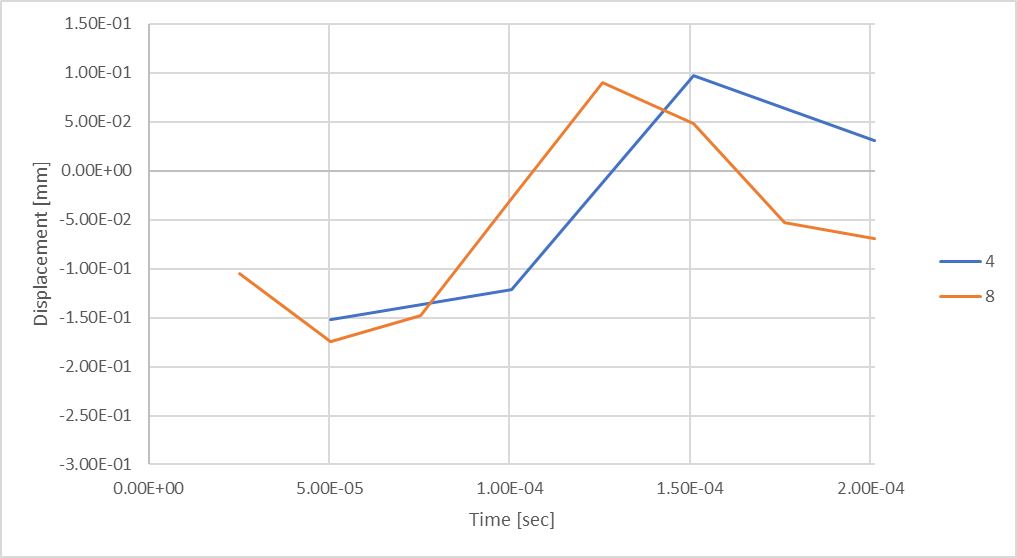
图 19:考虑 8 个时间步长时的杆位移。
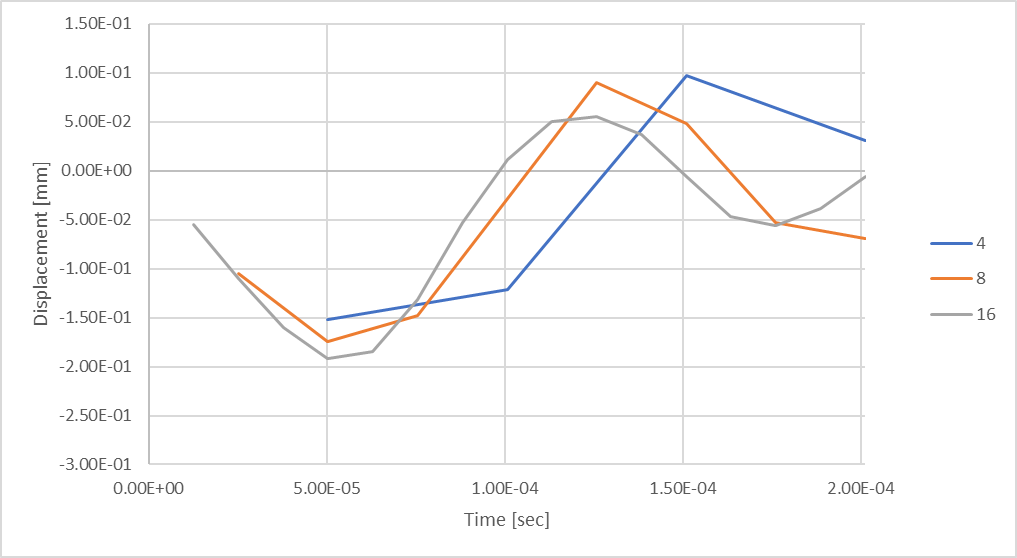
图 20:采用 16 个时间步长时,我们可以看到更大的杆压缩位移。
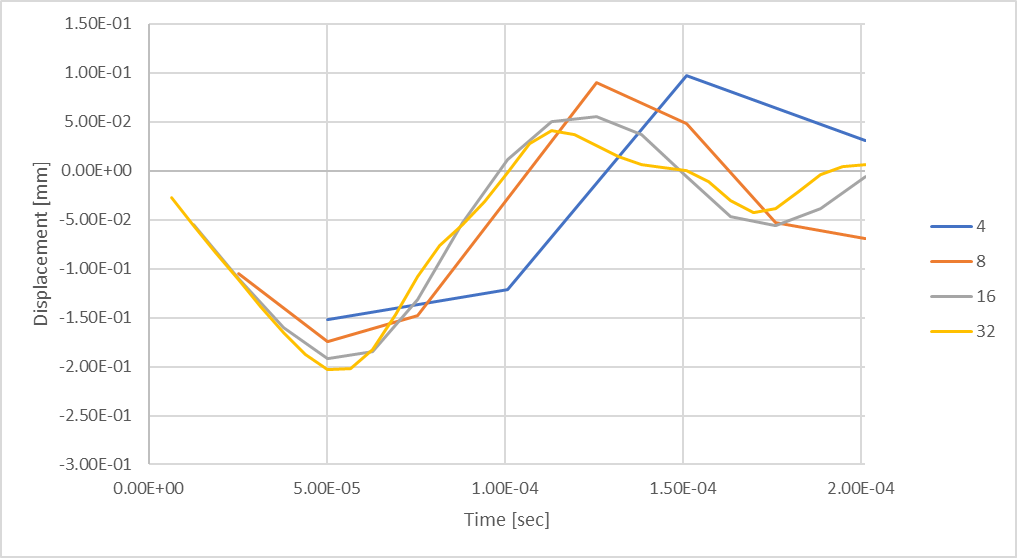
图 21:采用 32 个时间步长的瞬态最大杆挠度。
根据我们之前计算正弦波平均幅度的分析,我们发现,考虑 32 步,我们应该预计与理论结果最多相差 0.32%。 但是,我们可以看到,与之前的时间步长探索相比,我们的杆件压缩位移响应仍在形成中。 如果我们考虑更多的时间步长,会发生什么情况呢?
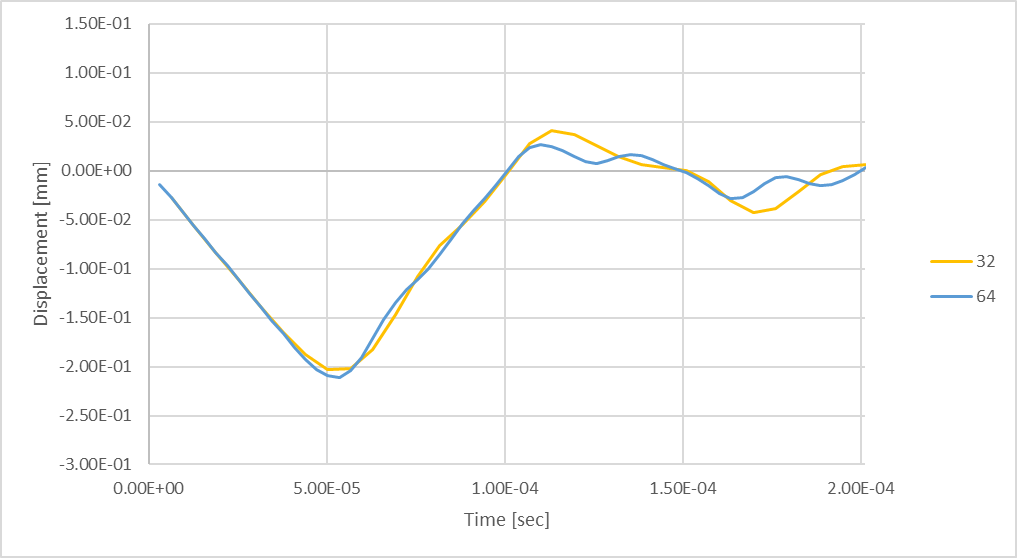
图 22:使用 64 个时间步长的瞬态最大杆挠度。
64 个时间步长产生的杆件最大压缩挠度稍大,但基本相似,不过在杆件回弹过程中出现了频率较高的振荡。
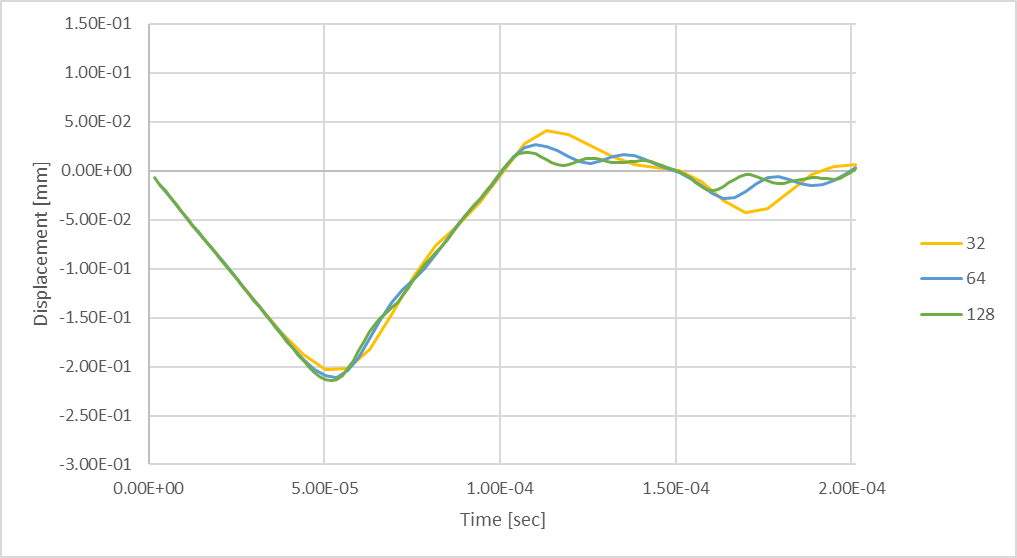
图 23:使用 128 个时间步长的瞬态最大杆挠度。
考虑 128 个时间步长时,轴的峰值压缩比考虑较少时间步长时大。 最大压缩挠度比 32 个时间步长时产生的挠度大 6%。
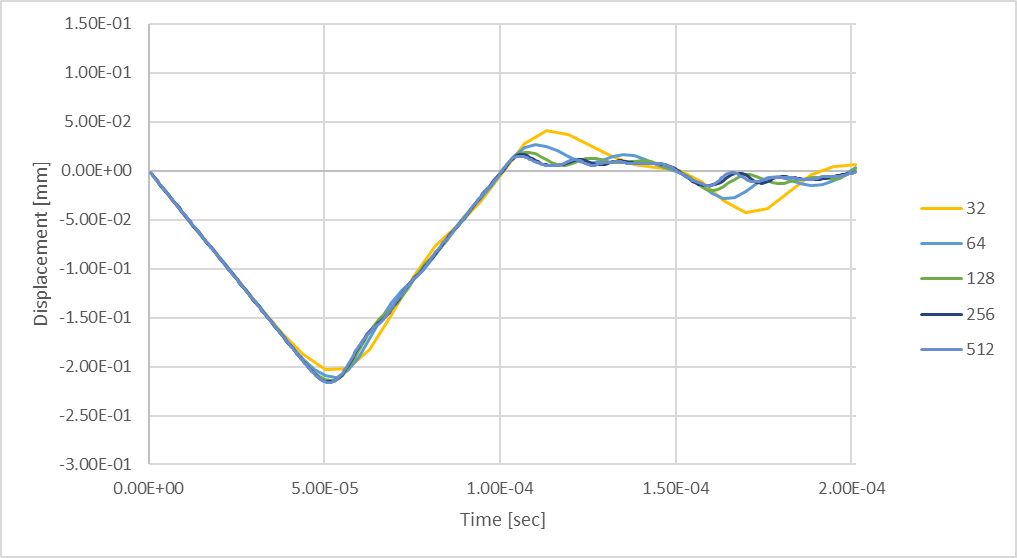
图 24:使用最多 512 个时间步长的瞬态最大杆挠度。
将 256 个时间步长的分析结果与 512 个时间步长的分析结果进行比较后发现,通过考虑更多的时间步长,可以计算出更高的动态响应分辨率。 下图说明了在瞬态结构分析中,最大杆件压缩挠度将如何随时间步数的变化而变化。
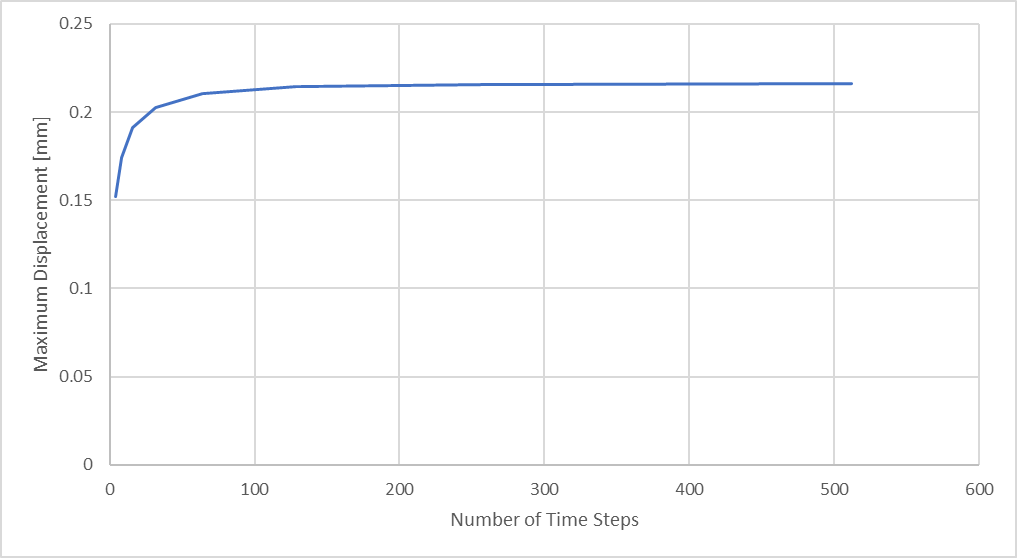
图 25:最大杆压缩位移与分析时间步数的关系
最终,对于给定的网格尺寸,我们会达到一个收益递减点……在这个点上,延长分析时间和增加结果文件所涉及的工作量并不能证明结果大小的显著变化是合理的。
基于这两点考虑,我们可以看到,通过使用 32 个时间步长,我们可以预期正弦曲线的特性最多相差 0.32%,但与使用 512 个时间步长的相同分析相比,位移结果的精度可能只有 94%,而与我们的理论最大挠度相比,精度也只有 91%。 我们可以从下图中看到最大杆压缩结果与理论最大值的比较。
| 子步骤数 | 最大压缩量 | 理论最大值 | 差异百分比 |
| 4 | 0.152139 | 0.222859 | 31.73% |
| 8 | 0.174023 | 0.222859 | 21.91% |
| 16 | 0.191486 | 0.222859 | 14.08% |
| 32 | 0.202746 | 0.222859 | 9.03% |
| 64 | 0.210712 | 0.222859 | 5.45% |
| 128 | 0.214455 | 0.222859 | 3.77% |
| 256 | 0.215752 | 0.222859 | 3.19% |
| 512 | 0.216232 | 0.222859 | 2.97% |
图 26:最大杆压缩位移 vs 分析时间步长
随着时间步数的增加,有限元分析结果与理论推导值之间的一致性也在增加。
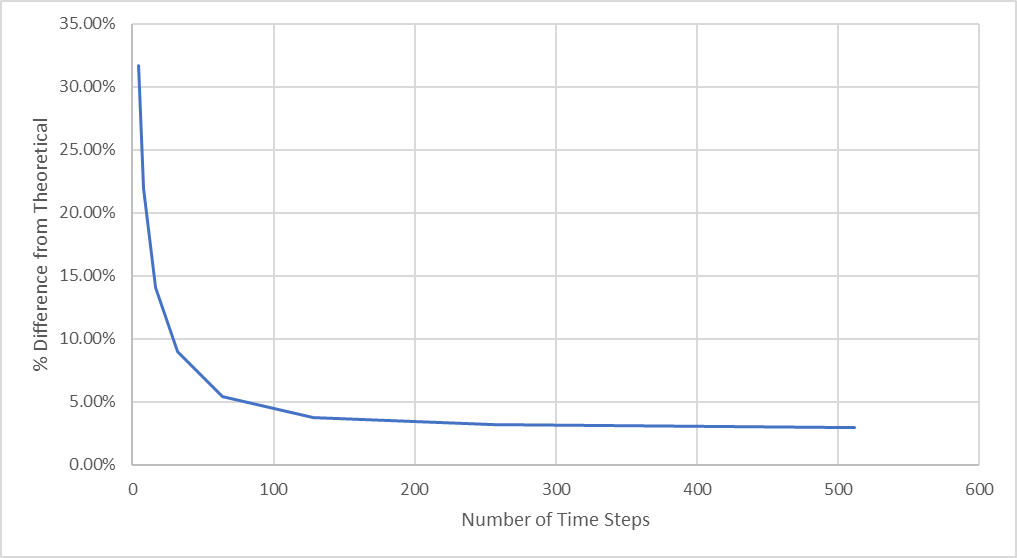
图 27:与理论最大挠度的百分比差异
从图中我们可以看出,当时间步数在 64 到 128 步之间时,收敛性有了显著提高,但随着时间步数的增加,变化很小。
但是,对于压力等其他结果来说,这些又意味着什么呢?
下面,我将绘制几种分析方案中每段时间的最大 von Mises 应力。
图 28:求解 32 个时间步骤时的 von Mises 应力
图 29:64 个时间步骤求解时的 von Mises 应力
图 30:求解 128 个时间步长时的 von Mises 应力
图 31:求解 256 个时间步长时的 von Mises 应力
图 32:求解 512 个时间步长时的 von Mises 应力
总之,这就是我们在查看应力时看到的情况:
| 子步骤数 | 最大平均应力 | 最大峰值应力 | 平均应力差 |
| 4 | 120.04 | 301.98 | 29.62% |
| 8 | 136.4 | 316.61 | 20.03% |
| 16 | 150.57 | 312.42 | 11.72% |
| 32 | 159.15 | 301.68 | 6.69% |
| 64 | 165.4 | 283.51 | 3.03% |
| 128 | 168.84 | 303.99 | 1.01% |
| 256 | 170.05 | 354.35 | 0.30% |
| 512 | 170.56 | 442.08 | 0.00% |
图 33:最大杆压缩位移与分析时间步数的关系
我们可以看到,随着时间步数的增加,冲击应力峰值也会变大,在冲击开始时显示出最大值,然后在整个过程中逐渐变小。 杆件中的平均应力确实从零上升到最大压缩时的峰值,然后在冲击结束后回落到零。 我们可以将这些最大平均应力绘制如下。
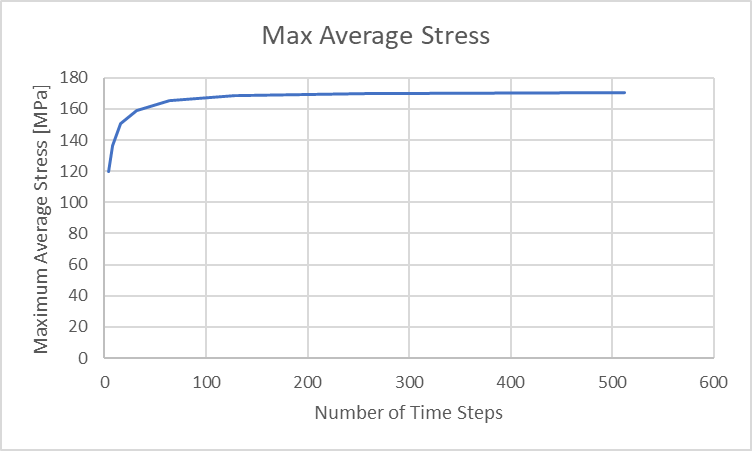
图 34:最大杆压缩位移 vs 分析时间步长
为了正确看待这些最大平均应力,我们可以计算出杆件的理论最大平均应力如下:
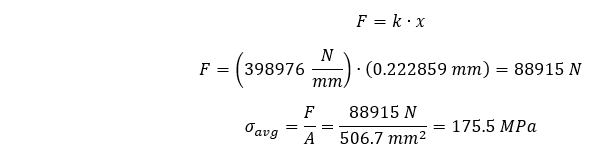
将我们的最大平均应力与理论计算出的最大平均应力进行对比,我们可以总结出以下的百分比差异:
| 子步骤数 | 最大平均应力 | 理论最大平均应力 | 差异百分比 |
| 4 | 120.04 | 175.5 | 31.60% |
| 8 | 136.4 | 175.5 | 22.28% |
| 16 | 150.57 | 175.5 | 14.21% |
| 32 | 159.15 | 175.5 | 9.32% |
| 64 | 165.4 | 175.5 | 5.75% |
| 128 | 168.84 | 175.5 | 3.79% |
| 256 | 170.05 | 175.5 | 3.11% |
| 512 | 170.56 | 175.5 | 2.81% |
图 35:最大杆压缩位移 vs 分析时间步长
与挠度分析一样,我们再次发现,在考虑 64 到 128 个事件时间步长的情况下,最大平均应力与理论计算的最大平均应力的百分比差异有了显著改善。 然而,使用更多的时间步长对我们结果的准确性几乎没有改善。
结论
我们验证了用于估算动态事件(例如弹性物体跌落到坚硬表面上)的最大偏转和平均应力的能量方法可能会产生合理的结果,并且在考虑 64 到 128 个时间步长时,精确度会有最显著的提高,该事件的周期等于我们根据撞击方向计算的撞击物体的固有频率。 我们还发现,逼近该固有频率的最佳方法不是手工计算,而是使用有限元方法进行模态分析,这主要是因为参与模态分析的有效质量可能不容易计算。

