mathematisch... aber in wirklichkeit ist es getan.
ich habe das beispiel für das nichtpräzise drehen gemacht, und es gibt andere beispiele für die verarbeitung von verbundwerkstoffen wie kohlenstoff- und glasfasern oder kunststoff-thermoformen.
es ist klar, dass wir von duktilen materialien sprechen, auf denen wir die verarbeitung durchführen können, ohne dass diese zerrissen oder ausgekratzt werden.
was ist das drehen in der platte?
wenn sie diese aussage nicht gemacht hätten, würde ich sagen, es ist eine schöne und gute ca@ata, aber angesichts der pulpe, aus der die informationen kommen, gehe ich mit den füßen der führung...
ich sage ihnen, was ich weiß, und auf dem ich spielen würde teile des körpers mehrere geliefert (so nur haare, haare, nägel, finger...pa@e no, um uns zu verstehen)
die oberflächen sind in erzielbare und unentwickelbare unterteilt. ausreichender zustand (aber nicht notwendig), so dass eine oberfläche entwickelt werden kann, ist eine einzige krümmung.
entwickelbare oberflächen können für plastische verformung gebaut werden, und der bereich der mittleren oberfläche ändert sich vor und nach der verformung nicht.
unentwickelbare oberflächen müssen eine variation der oberfläche zugeben, wenn sie auf dem boden und dann "richiuse" gebaut werden.
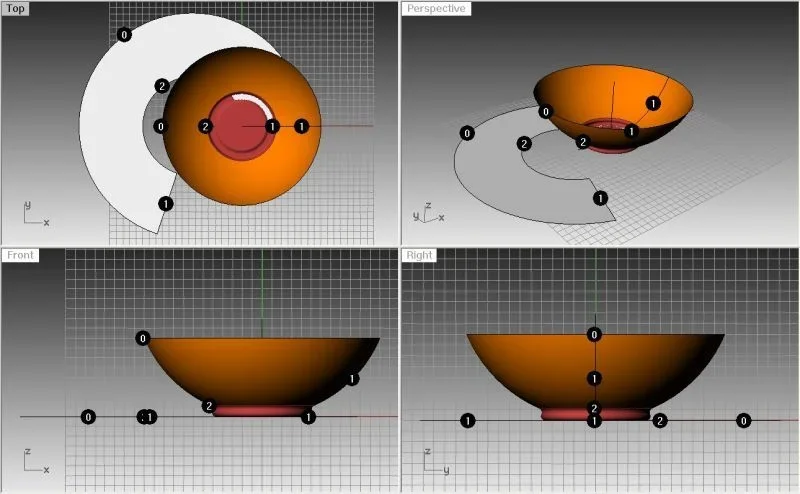
um uns zu sagen, wenn sie ein blatt nehmen und zu einer schüssel gehen, mit der "manischen" können sie einen halben ball tun, aber die halbe ballfläche wird höher als die der platte sein.
wenn du ein blatt papier nimmst, kannst du uns keinen halben ball geben.
das ist mein narr.