Taipan95
Guest
Guten Morgen.
wie aus dem Titel habe ich Zweifel an der Berechnung von Paaren (die dann dienen mir, um die Bäume zu überprüfen) in einem htd 3m Riementrieb, der verschiedene Riemenscheiben verbindet.
die Anwendung ist simil-printing, so haben wir eine Reihe von Bäumen mit gummierten Rollen calettati (die zu Kontrastrollen passen), die zur Bewegung von Papierblättern dienen. Deshalb gab ich an jedem Baum ein Paar "ca" an, das die Reibung zwischen den Gummiwalzen und den Kontrastwalzen wäre. Zusätzlich auf zwei Bäumen gibt es zusätzliche Belastungen (wegen anderer mechanischer Komponenten), die ich als "c1" und "c2"-Paare verwenden. das Antriebspaar des Systems wird "cm" genannt.
Ich stelle ein Bild des Getriebes, mit allen Riemenscheiben, die die gleiche Anzahl von Zähnen haben.
der erste Zweifel, der zu mir kommt, hängt mit der Spannung des Riemens zusammen: In einem zwei Riemenscheibensystem haben wir einen angespannteren Zweig mit der Spannung t1 und einen weniger angespannten Zweig mit der Spannung t2, aber in diesem Fall wie verhält sich die Spannung des Riemens? weil jeder Baum ein anderes Lastteil absorbiert, so denke ich, dass jeder Teil des Gürtels eine andere Spannung hat (die sich seltsam erweist, weil der Gürtel ein einzigartiger Körper ist...). Wenn ich die Spannung kenne, die ich brauche, weil die Spannung einen stechenden Moment auf dem Baum erzeugt, und ich muss es überprüfen. .
Der zweite Zweifel bezieht sich auf die Berechnung von Paaren "ca". durch experimentelle Tests, die wir am Motor gemessen haben, das zur Bewegung des gesamten Systems erforderliche Drehmoment cm, dann lösten wir den Benutzer 1 ab und gemessenen für die Differenz des verwendeten Drehmoments c1 und so auch für den Benutzer c2. Da die gummierten Rollen während der Übertragung gleich sind, würde ich das Paar ca auf den Bäumen tun (cm-c1-c2)/n. ist es korrekt als Verfahren?
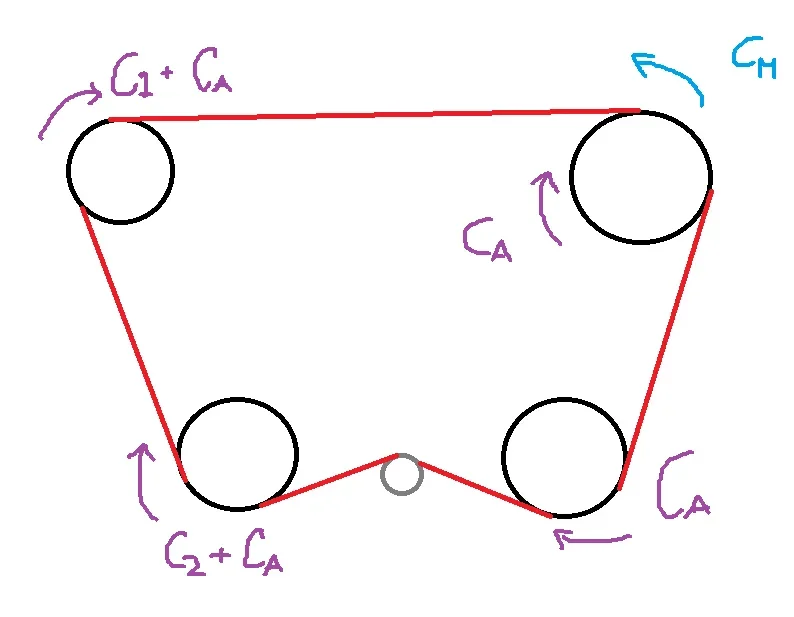
wie aus dem Titel habe ich Zweifel an der Berechnung von Paaren (die dann dienen mir, um die Bäume zu überprüfen) in einem htd 3m Riementrieb, der verschiedene Riemenscheiben verbindet.
die Anwendung ist simil-printing, so haben wir eine Reihe von Bäumen mit gummierten Rollen calettati (die zu Kontrastrollen passen), die zur Bewegung von Papierblättern dienen. Deshalb gab ich an jedem Baum ein Paar "ca" an, das die Reibung zwischen den Gummiwalzen und den Kontrastwalzen wäre. Zusätzlich auf zwei Bäumen gibt es zusätzliche Belastungen (wegen anderer mechanischer Komponenten), die ich als "c1" und "c2"-Paare verwenden. das Antriebspaar des Systems wird "cm" genannt.
Ich stelle ein Bild des Getriebes, mit allen Riemenscheiben, die die gleiche Anzahl von Zähnen haben.
der erste Zweifel, der zu mir kommt, hängt mit der Spannung des Riemens zusammen: In einem zwei Riemenscheibensystem haben wir einen angespannteren Zweig mit der Spannung t1 und einen weniger angespannten Zweig mit der Spannung t2, aber in diesem Fall wie verhält sich die Spannung des Riemens? weil jeder Baum ein anderes Lastteil absorbiert, so denke ich, dass jeder Teil des Gürtels eine andere Spannung hat (die sich seltsam erweist, weil der Gürtel ein einzigartiger Körper ist...). Wenn ich die Spannung kenne, die ich brauche, weil die Spannung einen stechenden Moment auf dem Baum erzeugt, und ich muss es überprüfen. .
Der zweite Zweifel bezieht sich auf die Berechnung von Paaren "ca". durch experimentelle Tests, die wir am Motor gemessen haben, das zur Bewegung des gesamten Systems erforderliche Drehmoment cm, dann lösten wir den Benutzer 1 ab und gemessenen für die Differenz des verwendeten Drehmoments c1 und so auch für den Benutzer c2. Da die gummierten Rollen während der Übertragung gleich sind, würde ich das Paar ca auf den Bäumen tun (cm-c1-c2)/n. ist es korrekt als Verfahren?