brn
Guest
Hallo an alle ich hätte ein triviales Problem mit excel (Ich bin kein Drache):
Ich mache eine Tabellenkalkulation, um die Öffnung eines Deckels mittels Zylindern zu simulieren.
Ich wollte ein Excel-Blatt machen, das die verschiedenen Parameter für jeden Öffnungsgrad des Deckels berechnet (oder für jeden Vorschub des Zylinders korrekter).
Ich stecke auf der Software-Ebene fest:
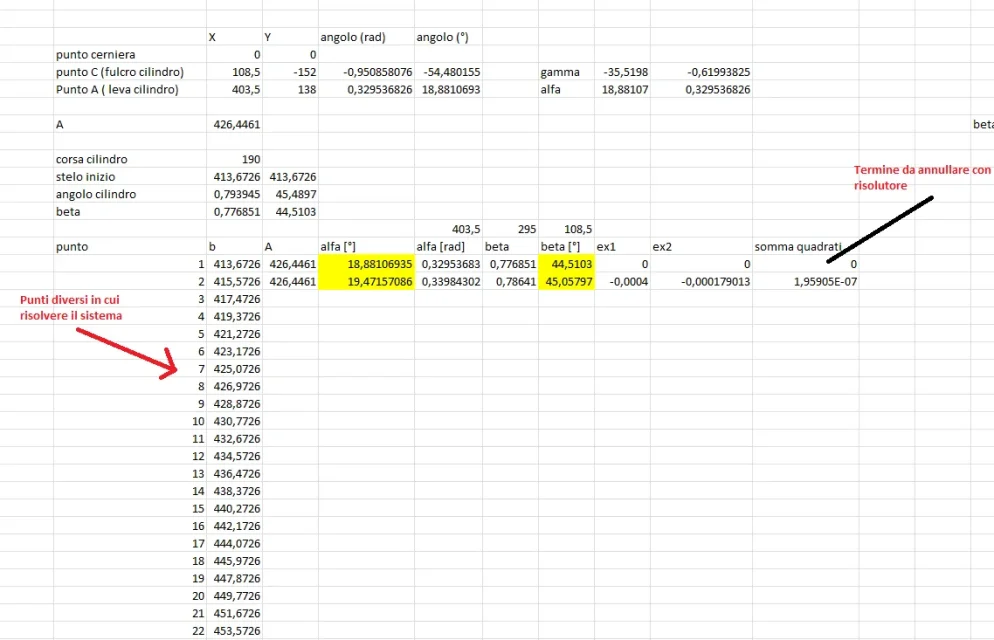
Daten zum Beispiel n Punkte, die das Rennen des Zylinders simulieren, für jeden möchte ich die Position berechnen, die durch das durch die Schließgleichungen gegebene System gegeben wird, dann von hier aus die Kräfte berechnen
a*cos(ANHANG)-b(t)*sen(Beta) = c*cos(gamma)
(a)ANHANG)-b(t)*sen(Beta) = c*sen(gamma)
mit alpha und beta incognite. Ich finde keine analytische Methode, um das System zu lösen (, aber ich bin sehr rustikal) daher wollte ich es Punkt für Punkt auf numerische Weise lösen, durch die Summe der Quadrate ist es trivial zu einem Problem mit dem Solvens gelöst zu kommen.
Aber hier ist das Problem: Wie kann ich in einem Excel-Blatt automatisch nichtlineare Systeme lösen?
wie kann ich vermeiden, den Resolver n-mal einzustellen?
für ein ähnliches Problem hatte ich ein Makro gesetzt, aber waren 5-6 Punkte nicht 100.
mit matlab oder ähnlich wäre ein triviales Problem mit einem Zyklus und einer Funktion, aber mit Excel Ich weiß nicht, wie es zu lösen
Vielen Dank
Ich mache eine Tabellenkalkulation, um die Öffnung eines Deckels mittels Zylindern zu simulieren.
Ich wollte ein Excel-Blatt machen, das die verschiedenen Parameter für jeden Öffnungsgrad des Deckels berechnet (oder für jeden Vorschub des Zylinders korrekter).
Ich stecke auf der Software-Ebene fest:
Daten zum Beispiel n Punkte, die das Rennen des Zylinders simulieren, für jeden möchte ich die Position berechnen, die durch das durch die Schließgleichungen gegebene System gegeben wird, dann von hier aus die Kräfte berechnen
a*cos(ANHANG)-b(t)*sen(Beta) = c*cos(gamma)
(a)ANHANG)-b(t)*sen(Beta) = c*sen(gamma)
mit alpha und beta incognite. Ich finde keine analytische Methode, um das System zu lösen (, aber ich bin sehr rustikal) daher wollte ich es Punkt für Punkt auf numerische Weise lösen, durch die Summe der Quadrate ist es trivial zu einem Problem mit dem Solvens gelöst zu kommen.
Aber hier ist das Problem: Wie kann ich in einem Excel-Blatt automatisch nichtlineare Systeme lösen?
wie kann ich vermeiden, den Resolver n-mal einzustellen?
für ein ähnliches Problem hatte ich ein Makro gesetzt, aber waren 5-6 Punkte nicht 100.
mit matlab oder ähnlich wäre ein triviales Problem mit einem Zyklus und einer Funktion, aber mit Excel Ich weiß nicht, wie es zu lösen
Vielen Dank