Asynchronmotordimensionierung mit Sinuslast

[meccanicamg]

hier ist ein Ansatz, um das Drehmoment an der Kurbel Ihres Biella-Manovella-Mechanismus zu berechnen:
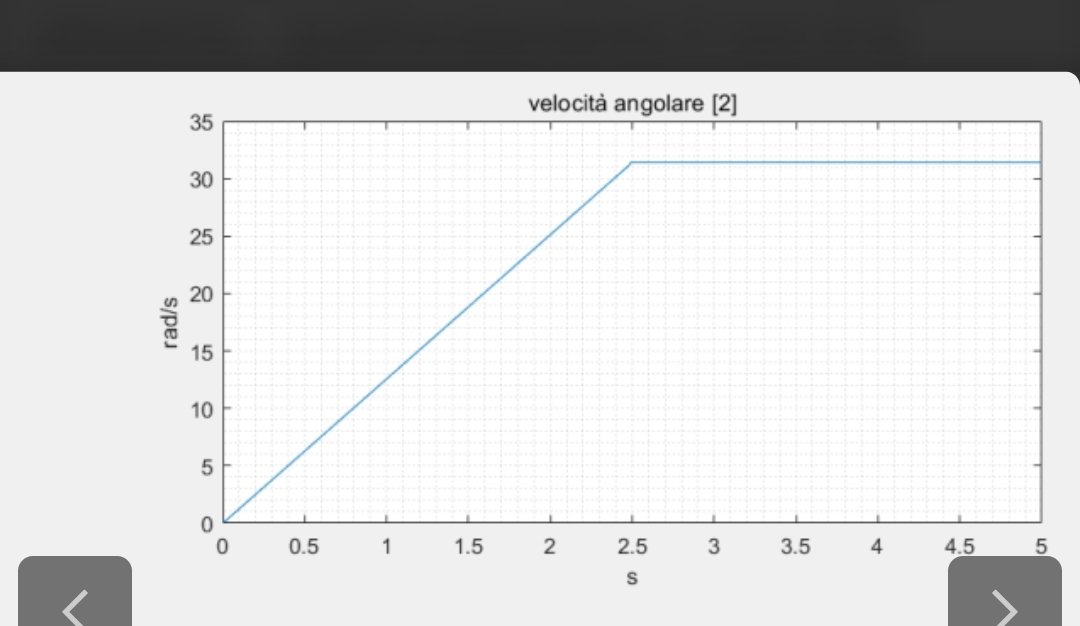
1. Berechnung der Winkelbeschleunigung:* Umwandlung von Windungen pro Minute zu Strahlung pro Sekunde: 1 min/60 s ≈ 31,42 rad/s
* Berechnung der Winkelbeschleunigung: α = ω / t = 31.42 rad/s / 2.5 s ≈ 12.57 rad/s2
2. Kraftberechnung auf den Kolben:* Bestimmung der zur Beschleunigung der Masse erforderlichen Kraft: f = m
* Berechnung der Linearbeschleunigung des Kolbens: Dies ist ein komplexerer Teil, da die Beschleunigung des Kolbens während der Drehung der Kurbel variiert. für eine ungefähre Schätzung können Sie die maximale Beschleunigung des Kolbens betrachten, die auftritt, wenn die Kurbel senkrecht zur Biella ist. Sie können eine detailliertere Filmanalyse für eine genauere Berechnung verwenden.
3. Berechnung der Tangentialkraft am Handgriff:* Verwendung des Übersetzungsverhältnisses: Die Kraft auf den Kolben wird durch die Biella auf die Kurbel übertragen. das Übersetzungsverhältnis zwischen der Kraft auf den Kolben und der Tangentialkraft auf den Handgriff hängt von der Geometrie des Mechanismus (Länge der Biella und des Griffbalkens) ab.
* Tangentiale Kraftberechnung: f_tangenziale = f_pistone * (r_manovella / l_biella)
4. Berechnung des Drehmoments zum Handgriff:* Drehmomentdefinition: Das Paar ist das Produkt der Tangentialkraft für den Kurbelradius.
* Drehmomentberechnung: τ =
zusammenfassende Formeln:
* ω = 2πn / 60
*
* f = m * a
* f_tangenziale = f_pistone * (r_manovella / l_biella)
* τ = f_tangen * r_manovella

Kommentare:
* Näherung: Diese Berechnung liefert eine ungefähre Schätzung des Paares. für ein genaueres Ergebnis ist es erforderlich, die vollständige kinematische Analyse des Biella-Manovella-Mechanismus unter Berücksichtigung der Veränderung der Beschleunigung des Kolbens bei der Drehung der Kurbel zu berücksichtigen.
* Andere Faktoren: Andere Faktoren wie Reibung, Biellamasse und Verluste im Mechanismus können das tatsächliche Drehmoment beeinflussen.

Eine genaue Berechnung der Beschleunigung des Kolbens in einem Biella-Manovella-Mechanismus erfordert eine eingehendere Analyse der Kinematik.

Formeln und Erwägungen:zur Ermittlung der Beschleunigung des Kolbens zu jedem Zeitpunkt ist es erforderlich, die Geometrie des Mechanismus und die Winkelgeschwindigkeit des Handgriffs zu berücksichtigen.* Kolbenstellung:
die Lage des Kolbens (s) gegenüber dem oberen Totpunkt kann nach dem Drehwinkel der Kurbel (θ) und den Längen der Biella (l) und der Kurbel (r) ausgedrückt werden:
(cos(θ) + √(l2 - r2sin2(θ)))

* Kolbengeschwindigkeit:
die Position im Vergleich zur Zeit ermittelt, erhalten Sie die Kolbengeschwindigkeit:
v = ds/dt = ω * r * (sin(θ) + (r * sin(θ) * cos(θ) / √(l2 - r2sin2(θ)))

wobei ω die Winkelgeschwindigkeit der Kurbel ist.
* Kolbenbeschleunigung:
weiter die Geschwindigkeit im Vergleich zur Zeit, erhalten Sie die Beschleunigung des Kolbens:
a = dv/dt = ω2 * r * (cos(θ) + (r * (cos2(θ) - sin2(θ))) / √(l2 - r2sin2(θ))) + (r3 * sin2(θ) * cos(θ)) / (l2 - r2sin2(θ))))^(3/2))

Kommentare:
* Komplexität der Gleichung: Wie Sie sehen können, ist die Beschleunigungsgleichung ziemlich komplex und enthält trigonometrische Begriffe.
* Beschleunigungsvariation: Die Beschleunigung des Kolbens variiert während der Drehung der Kurbel kontinuierlich, erreicht maximale und minimale Werte an bestimmten Positionen.
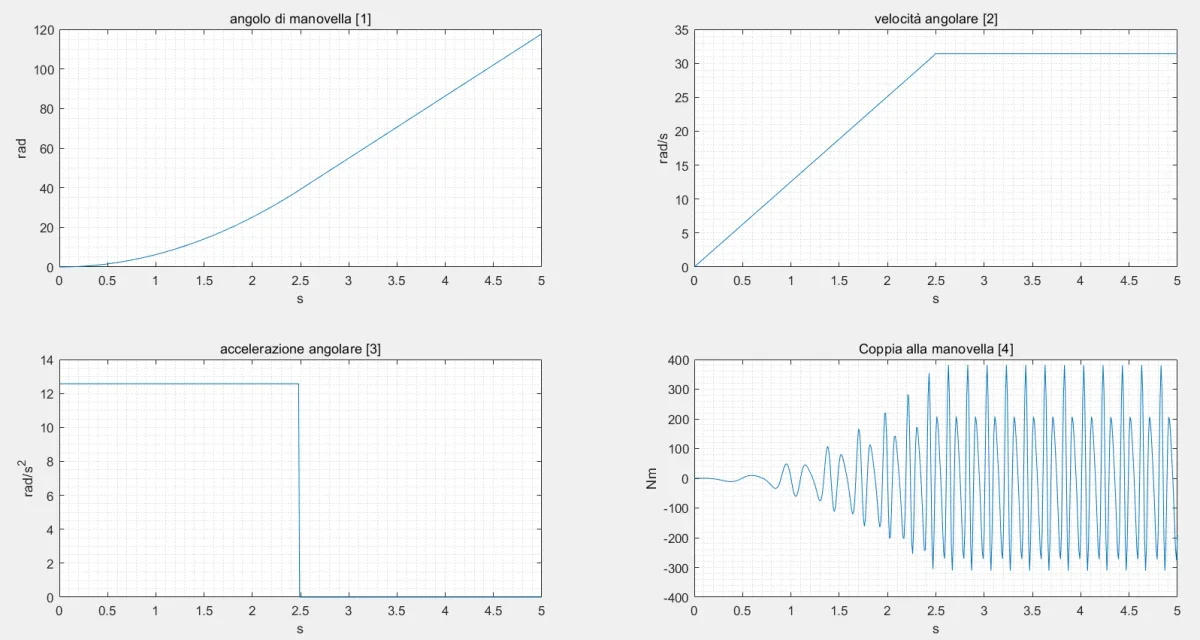
* Grafiken: Um die Beschleunigungsvariation über die Zeit besser anzuzeigen, ist es sinnvoll, die Beschleunigung nach dem Drehwinkel des Handgriffs grafisch darzustellen.

numerische Berechnungen:
um bestimmte Zahlenwerte für Ihren Fall zu erhalten, können Sie:
* Ersetzen Sie Zahlenwerte: setzen Sie r, l, ω und θ Werte in Gleichungen ein.
* Verwenden Sie ein Tabellenblatt: Verwenden Sie ein Programm wie Excel oder ein Online-Tabellenblatt, um Beschleunigung für verschiedene Werte von θ zu berechnen.
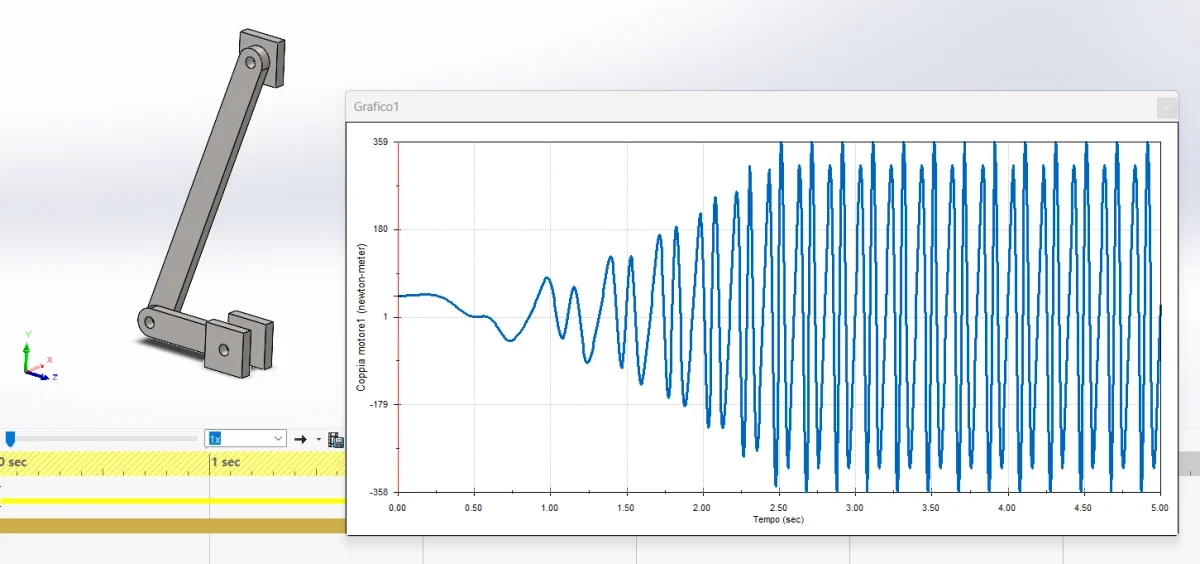
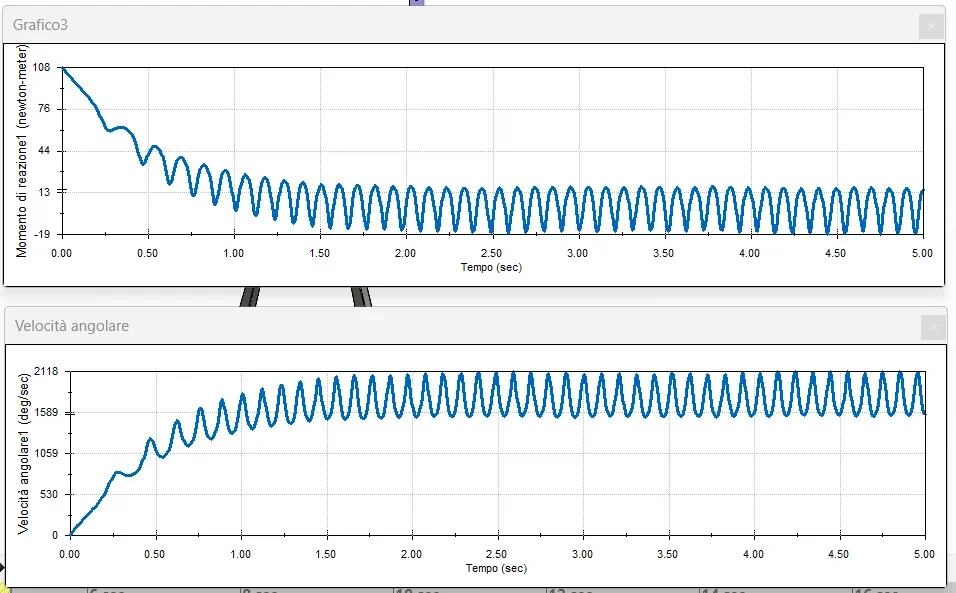
* Verwenden Sie eine Simulationssoftware: Software wie Matlab oder Cad-Programme können verwendet werden, um dynamische Simulationen des Mechanismus durchzuführen und detaillierte Grafiken der Beschleunigung zu erhalten.

Weitere Überlegungen:
* Drehwinkel: θ Winkel kann von 0 bis 2 Strahlung für eine vollständige Drehung der Kurbel variieren.
* Messeinheit: Achten Sie darauf, konsequente Messeinheiten (z.B. Meter für Längen, Strahlmittel für Winkel und Sekunden für Zeit) zu verwenden.
* Näherung: In einigen Fällen können Approximationen verwendet werden, um Berechnungen zu vereinfachen, aber es ist wichtig, die Genauigkeit der Approximationen entsprechend der spezifischen Anwendung zu bewerten.

tun alles mit Excel und Sie werden sehen, dass Sie in der Lage sein, die Diagramme, die Sie benötigen, zu verfolgen und dann von hier überschneiden die Motorkurve Leistung / Drehungen und Drehmoment / Drehungen und Sie werden beurteilen, ob es okay ist oder nicht.

Denken Sie daran, dass Sie je nach Startwinkel immer noch verschiedene Diagramme und Drehmomente erhalten, um unterschiedlich zu starten.

in all dies in der ersten unbeeinflussten Näherung betrachtet wurde: Reibung und Trägheit.

baute das Grundrechnungsblatt, das Sie mit neuen Überlegungen bereichern können.

 

[Taipan95]

Guten Morgen.
Dank für alle Ihre Überlegungen und Beiträge. Ich schuf eine kleine Liste von Matlabs, wo ich ging, um die Gleichungen des Problems (der Allego) einfügen.
Grundsätzlich berechnete ich die vertikale Beschleunigung des Kolbens, der die sekundäre Ableitung seiner Position im Raum durchführt, die auf derta und phi parametriert ist (siehe Abbildung I am Anfang der Post). Ich verhängte das Beschleunigungsprofil und rückwärts bestimmt, numerisch, die Geschwindigkeit und Winkelstellung der Kurbel. auch der phi-Winkel wurde im Vergleich zu theta parametriert, sowie auf numerische Weise wurden seine Derivate bestimmt (Geschwindigkeit und Beschleunigung).

An dieser Stelle schrieb ich die Massengleichung* Beschleunigung = Kolbenkraft, die ich in tangentiale Kraft umgewandelt habe. Das, multipliziert mit Kurbel, gab mir das Paar.

Darstellung der Diagramme: Winkelbeschleunigung der Kurbel (1), Geschwindigkeit (2), kumulativer Winkel (3) [tutte in rad], und schließlich das Fahrpaar (4) [in Nm].

Ich versuchte, in Solidworks ein sehr einfaches System zu modellieren, und mit dem Bewegungsmodul simulierte ich es, indem ich das Geschwindigkeitsprofil von mir wollte (von 0 auf 2,5 s kletterst du auf 300 pm, dann gehst du konstant von 2,5s auf 5s).

Wie Sie sehen können, sind die beiden Trends identisch in Form und sehr ähnlich in Werten (weniger Unterschiede aufgrund von Trägheit, dass in meinen Konten gibt es keine... Reibung ist nicht einmal in Festkörpern).

Und hier gehen wir zurück zu dem, was ich von Anfang an zu erklären versuchte, aber das wegen mir vielleicht nicht gut kam... Wie kommt es, um dieses System von 20kg zu bewegen, brauche ich ein paar in der Größenordnung von 400nm? klar ist es nicht richtig... Die Antwort, die ich mir gegeben habe, ist wie folgt: weil das System eine oszillierende Dynamik hat, wenn ich einen sofortigen Geschwindigkeitstrend aufzwinge wie in (3) Ich muss ein sehr hohes Drehmoment bereitstellen... dieser Trend gibt es nicht sofort Geschwindigkeit, aber es sollte die mittlere Geschwindigkeit sein, um die ich die Schwingungen habe (und das war, was ich vor der schwarzen Linie und dem roten Sinusoid geschrieben hatte).

 

[meccanicamg]

Guten Morgen.
Dank für alle Ihre Überlegungen und Beiträge. Ich schuf eine kleine Liste von Matlabs, wo ich ging, um die Gleichungen des Problems (der Allego) einfügen.
Grundsätzlich berechnete ich die vertikale Beschleunigung des Kolbens, der die sekundäre Ableitung seiner Position im Raum durchführt, die auf derta und phi parametriert ist (siehe Abbildung I am Anfang der Post). Ich verhängte das Beschleunigungsprofil und rückwärts bestimmt, numerisch, die Geschwindigkeit und Winkelstellung der Kurbel. auch der phi-Winkel wurde im Vergleich zu theta parametriert, sowie auf numerische Weise wurden seine Derivate bestimmt (Geschwindigkeit und Beschleunigung).

An dieser Stelle schrieb ich die Massengleichung* Beschleunigung = Kolbenkraft, die ich in tangentiale Kraft umgewandelt habe. Das, multipliziert mit Kurbel, gab mir das Paar.

Darstellung der Diagramme: Winkelbeschleunigung der Kurbel (1), Geschwindigkeit (2), kumulativer Winkel (3) [tutte in rad], und schließlich das Fahrpaar (4) [in Nm].

Ich versuchte, in Solidworks ein sehr einfaches System zu modellieren, und mit dem Bewegungsmodul simulierte ich es, indem ich das Geschwindigkeitsprofil von mir wollte (von 0 auf 2,5 s kletterst du auf 300 pm, dann gehst du konstant von 2,5s auf 5s).

Wie Sie sehen können, sind die beiden Trends identisch in Form und sehr ähnlich in Werten (weniger Unterschiede aufgrund von Trägheit, dass in meinen Konten gibt es keine... Reibung ist nicht einmal in Festkörpern).

Und hier gehen wir zurück zu dem, was ich von Anfang an zu erklären versuchte, aber das wegen mir vielleicht nicht gut kam... Wie kommt es, um dieses System von 20kg zu bewegen, brauche ich ein paar in der Größenordnung von 400nm? klar ist es nicht richtig... Die Antwort, die ich mir gegeben habe, ist wie folgt: weil das System eine oszillierende Dynamik hat, wenn ich einen sofortigen Geschwindigkeitstrend aufzwinge wie in (3) Ich muss ein sehr hohes Drehmoment bereitstellen... dieser Trend gibt es nicht sofort Geschwindigkeit, aber es sollte die mittlere Geschwindigkeit sein, um die ich die Schwingungen habe (und das war, was ich vor der schwarzen Linie und dem roten Sinusoid geschrieben hatte).

die 400nm sind diejenigen, die der Umkehr der Bewegung entsprechen. In diesem Moment, bei konstanter Kurbelgeschwindigkeit, haben Sie einen Trend weit davon entfernt, die Masse des Kolbens auszuüben. der Kolben geht von vorne auf v max auf Null und plötzlich minus v max.
Ihr Motor oder der Reduzierer muss 400nm liefern.

Reduktionsverhältnis:
= 1400/300 = 4,7

Motor 4 Pole n=1400rpm
Motordrehmoment = 400/4,7 = 85nm
Leistung sterben über wm = 12.5kw

seit 12.5kw gibt es keine 11kw, die Standard ist und wir verwenden es mit den Inversionen über s1. Eigentlich könnten Sie auch eine 7,5kw 4p mit der gleichen Logik verwenden.

Wenn Sie eine Vektor-Engine bevorzugen, können wir eine Basisdrehzahl höher 2000....3000rpm verwenden und dann ein Getriebe mit größerem und einfacherem Lieferverhältnis verwenden.

mit solidworks bewegen den Mechanismus und sehen, welche Positionen den Spitzen von +/-400nm entsprechen und posten das Bild.

 

[meccanicamg]

Dieser angesetzte Getriebemotor stellt beispielsweise einen Standard-Seg-Motor mit Koaxial-Reduktionsgerät mit einem 4 Polmotor und ein Reduktionsverhältnis dar, das die gleiche Abtriebsdrehzahl bewirkt.

 

[Taipan95]

Ich stelle Ihnen einen Screenshot eines sehr ähnlichen Mechanismus (sofern die Trägheit nicht, aber jetzt lassen wir sie ignorieren), der während des Kurses gezeigt wurde, den ich verfolgte.

wie Sie sehen, simuliert in Solidworks Bewegung, ist der durchschnittliche Geschwindigkeitstrend genau das, was Sie wollen, aber sofort dreht es um diesen Wert (im Bereich zwischen 2100 und 1500, dessen Durchschnitt ist 1800 [gradi al secondo] das sind nur 300 rpm) anstatt linear und genau wie die Trends, die ich vor in matlab veröffentlicht.

wenn bekannt, das benötigte Paar ist oszillierend, aber es erreicht maximal 20nm (unterlassen des Punktwertes, konzentrieren sich nur auf das Regime)... Wie ist es möglich? die Einstellung mit Inverter erlaubt mir dies zu tun?

Ich kann nicht verstehen, wie es möglich ist, dass Sie eine so hohe Drehmomentdiskretion erhalten (400nm mit einem linearen Geschwindigkeitsprofil gegen 20nm eines Oszillators, von dem der Durchschnitt ist, was mich interessiert, aber nicht der momentane Wert... In der Tat ist das durchschnittliche Geschwindigkeitsprofil genau wie die, die ich wollte, es bringt uns etwa 2s zu Regime und von dort geht... Ich akzeptiere, dass es sofort Schwingungen gibt, es ist der Durchschnitt in der Zeit, die mir wichtig ist.

und dies rechtfertigt die Tatsache, dass der Asynchronmotor, der mit Inveter, dieser in Wirklichkeit realisierten Anwendung, ist Gips bis 1kw der Leistung, die sich von der 12kw unterscheidet, die wir mit den "manuellen" Konten finden.

 

[meccanicamg]

Ich fürchte, ich verstehe nicht.
mit dem Wechselrichter, wenn es Meister ist, verhängen Sie, was es tun muss und wenn es in seinem Strom ist, tut er. Hier können Sie einen Positionierer als Achse einstellen und steuern.
Wenn es Sklave eine Grenze hat und natürlich das System selbst ausgleicht, aber s1 nicht überschreitet, wird langsam die Trägheit gewinnen und flach wird zum Regime kommen.
Schauen Sie, dass die Trägheit des Kolbens das ist, was die Drehmomentbelastung des Motors....so vernachlässigbar ist nicht.
Dann wiederhole ich die Frage, die du nicht beantwortet hast: Sinus ist die Umkehr der Bewegung, wenn die Last am Boden der Extreme ankommt?
Wenn du... Die Inversionsbeschleunigung ist praktisch doppelt. und aber eine schöne Kurbel hat die Beschleunigungen des nichtlinearen Kolbens und nicht konstant, wenn der Motor mit konstanter Geschwindigkeit dreht.

 

[meccanicamg]

Lineares Profil? oszillierendes Profil? Was?
Ich glaube, du verwirrst Dinge oder ich bekomme nichts mehr.

 

[Taipan95]

Ich versuche, mich besser zu erklären: In früheren Beiträgen habe ich zwei Geschwindigkeitsprofile gesetzt, beides ähnlich, weil von 0 bis 2,5s beleuchtet und dann von 2,5s gehe ich zum Regime... Der einzige Unterschied ist, dass einer von ihnen momentane Schwingungen hat, aber sein Durchschnittswert folgt immer noch diesem Trend. hatte, der gleiche Mechanismus, aber vorbehaltlich dieser beiden Gesetze hat sehr unterschiedliche bewegte Paarwerte. Wie kommt's?

 

[Taipan95]

Konkret beziehe ich mich auf diese beiden Geschwindigkeitsprofile... bei Regime sind beide 300rpm, nur einer ist Durchschnittswert, weil sofort Swings hat, während der andere ist 300 pünktliche roms

 

[Taipan95]

Stellen wir uns vor, dass sie uns diese beiden Geschwindigkeitstrends zeigen... in unserer Anwendung ist es nicht wichtig, dass Sie eine super präzise Kontrolle über Geschwindigkeit haben, solange der Durchschnitt den gewünschten Trend respektiert (0 2,5s accelero, dann nehme ich an Regime). vor diesem kleinen Detail, das ist die Tatsache, dass ich den Durchschnitt habe, der den Trend respektiert und nicht die momentanen pünktlichen Werte, das erforderliche Paar fällt drastisch, so dass der Motor zu verwenden ist viel kleiner. Wie ist es möglich, dass Sie nur einige Schwungen im Geschwindigkeitsprofil haben, um das Paar so viel zu senken?

 

[meccanicamg]

Heute schaffte ich es, Simulationen mit Siemen-Größer zu machen. wir haben zwei Szenarien, aber immer mit der gleichen mechanischen Anwendung: biella Griff mit 20 kg vertikal. Geometrie, die Sie mir 175mm Kurbel und 517mm Biella geliefert.
2,5s von einem Anschlag zu erreichen 300rpm an der Kurbel 31,4rad/s und Rampen mit 12,5m/s2.
Motoriduttor Servo mit hochdichtem bürstenlosen Drehmomentmotor, automatisch von Computer 1,82kw-3000rpm und i=10,53 Reduzierer gewählt.
wie Sie sehen, mit niedrigen Trägheit und Drehmoment übertrieben sogar 4 mal den nominellen Sie tun, was Sie mit Spitzen wollen.
Drehstrom-Asynchronmotoren ein Eichhörnchenkäfig. mehr Trägheit und weniger müssen sich paaren zu verwenden. der Wähler wählte ein 7,5kw -1308rpm und Reduzierer i=4,36. praktisch die Lösung, die ich Ihnen von Hand gab.
wie Sie sehen, nutzt er es auch über s1 um die Starterspitzen zu verwalten.
wir haben zwei Spitzen für jedes Erreichen des Endes des Kolbens, dann eine halbe Periode der Kolbenbewegung.

wie Sie sehen, die Theorie ist immer, aber es hängt davon ab, welche Motor Sie zur Verfügung haben, um die durchschnittliche Leistung der ich denke, die Aktion zu verwalten.

 

[meccanicamg]

Heute schaffte ich es, Simulationen mit Siemen-Größer zu machen. wir haben zwei Szenarien, aber immer mit der gleichen mechanischen Anwendung: biella Griff mit 20 kg vertikal. Geometrie, die Sie mir 175mm Kurbel und 517mm Biella geliefert.
2,5s von einem Anschlag zu erreichen 300rpm an der Kurbel 31,4rad/s und Rampen mit 12,5 m/s2.

Motor Servomotor mit hochdichtem bürstenlosen Drehmomentmotor, automatisch von Computer 1,82kw-3000rpm und i=10,53 Reduzierer gewählt.
Anhang anzeigen 72165wie Sie sehen, mit niedrigen Trägheit und Drehmoment übertrieben sogar 4 mal den nominellen Sie tun, was Sie mit Spitzen wollen.
Drehstrom-Asynchronmotoren ein Eichhörnchenkäfig. mehr Trägheit und weniger müssen sich paaren zu verwenden. der Wähler wählte ein 7,5kw -1308rpm und Reduzierer i=4,36. praktisch die Lösung, die ich Ihnen von Hand gab.
Anhang anzeigen 72166wie Sie sehen, nutzt er es auch über s1 um die Starterspitzen zu verwalten.
Anhang anzeigen 72167wir haben zwei Spitzen für jedes Erreichen des Endes des Kolbens, dann eine halbe Periode der Kolbenbewegung.

wie Sie sehen, die Theorie ist immer, aber es hängt davon ab, welchen Motor Sie zur Verfügung haben, um die durchschnittliche Leistung zu verwalten Ich glaube die Aktion.

falscher Kurier für Beschleunigung... es ist nicht m/s2 aber Rad/s2.

ist nicht "Ich glaube, die Aktion" sondern "Leistung".

Es tut mir leid. Ich schrieb im Regen, der das Telefon brach.

 

[Taipan95]

Kann ich Sie fragen, wo ich die Version von Siemen Größer finden Sie verwenden? Ich versuchte, es im Internet zu suchen, aber von dem, was ich sah, war es in eine Art neues Werkzeug von Siemen integriert, die, obwohl ich versuchte, herunterzuladen, aber es scheint wirklich unverständlich. . Ich möchte versuchen, Ihre Simulationen zu replizieren

einmal mache ich das, vielleicht höre ich auf und es geht ihnen gut.

Danke.

 

[meccanicamg]

Sie finden qui. nach Registrierung. Version 3.23.

 

[Esselle]

Sie finden qui. nach Registrierung. Version 3.23.

Ich habe überall gesucht, aber der Link zum Download ist nicht gefunden....

 

[Taipan95]

auf der Seite steht, dass es in das Tia-Tool der Siemen integriert wurde... und es gibt den Link, der Sie auf die Tia-Tool-Seite verbindet.

das Problem ist, dass ich Werkzeug ist nicht intuitiv zu bedienen, es scheint ziemlich kompliziert

 

[Esselle]

auf der Seite steht, dass es in das Tia-Tool der Siemen integriert wurde... und es gibt den Link, der Sie auf die Tia-Tool-Seite verbindet.

das Problem ist, dass ich Werkzeug ist nicht intuitiv zu bedienen, es scheint ziemlich kompliziert

Okay, danke, dass ich da bin, aber ich sah siemens Größer ich wurde verwirrt. Es gibt tatsächlich so viele Funktionen, es muss zuerst mit jemandem verwendet werden, der Sie leiten kann, denke ich.

 

[Taipan95]

innerhalb des tia-Tools gibt es einen Teil des "Größe-Laufwerks mit Größer", aber anscheinend ist eine Registrierung im Siemenportal erforderlich... Sie müssen Ihre personenbezogenen Daten eingeben und es sagt, dass, wenn die Analyse der Daten korrekt ist, innerhalb von wenigen Tagen können Sie herunterladen.

Ich warte auf Updates, in der Hoffnung, dass das Verfahren die richtige ist..

 

[Esselle]

Du könntest versuchen, ob Rockwell-Software für dich kongenialer ist.
Rockwell

 

[meccanicamg]

innerhalb des tia-Tools gibt es einen Teil des "Größe-Laufwerks mit Größer", aber anscheinend ist eine Registrierung im Siemenportal erforderlich... Sie müssen Ihre personenbezogenen Daten eingeben und es sagt, dass, wenn die Analyse der Daten korrekt ist, innerhalb von wenigen Tagen können Sie herunterladen.

Ich warte auf Updates, in der Hoffnung, dass das Verfahren die richtige ist..

nie verwendet...in den nächsten Tagen möchte ich wirklich sehen, ob es besser sein kann als das separate Werkzeug, das ich immer verwendet habe.

Natürlich auch der Größer allein....intuitiv für nichts. Man braucht jemanden, der weiß, wie man es benutzt....oder man muss ein elektrischer Agent sein... aber wenn man lernt, dann erkennt man, dass es einfach ist, auch wenn nicht intuitiv.