Der bescheidene Diener

[Fulvio Romano]

SteuerungBisher haben wir über den Manipulator gesprochen. Fangen wir an, über die Hälfte des Roboters zu reden.
der Controller, der zusammen mit dem Manipulator gekauft wird, ist der elektronische Teil, der sich mit Motorleistung, Feedback-Datenmanagement usw. befasst. wir sehen, aus welchen Elementen sie besteht.
KleiderschrankDer Schrank ist die elektrische Platte, die das elektronische Teil enthält. außen hat einen Notfallpilz, einen Schlüsselmodus-Selektor (obligatorisch nach der Norm), oft einen Operationszähler und Steckverbinder für externe Geräte. hat oft einen Ethernet-Sockel und einen USB-Anschluss zum Anschluss von Peripheriegeräten.
innen besteht der Schrank aus folgenden Makroblöcken:
Computerein industrieller PC beschäftigt sich mit der realen Kontrolle des Manipulators. es implementiert die Algorithmen der filmischen Inversion, Kontrolle, der Dolmetscher der Programmiersprache, die Verwaltung der Peripherie, etc. in der Praxis beschäftigt es sich mit der logischen Verwaltung von allem, was den Roboter betrifft, ohne die Sicherheit. Diese werden über Hardware von einer bestimmten Karte bearbeitet.
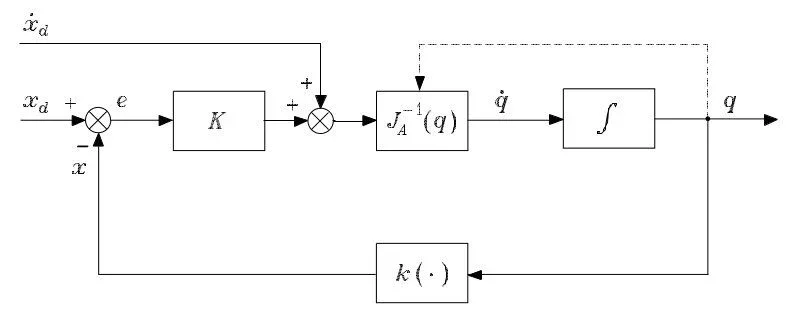
Pappedie Achskarte nimmt die Eingangsreferenzen von Position, Geschwindigkeit und Beschleunigung ein, die der Rechner entscheidet, die Motoren zu haben, und erhält auch die Daten der empfangsfähigen Sensoren des Roboters (Encoder oder Resolver). die Differenz zwischen den beiden ist der sogenannte "Fehler", wonach es notwendig ist, die Motoren zu pilotieren, so dass die Bewegung des Roboters die gewünschte ist, d.h. der Fehler wird innerhalb einer akzeptablen Schwelle gehalten. Eigentlich wird ein Teil der Kontrolle durch den PC durchgeführt, und es beginnt von der Board-Tab, aber für eine detailliertere Beschreibung werde ich versuchen, etwas weiter zu schreiben. es wird nicht einfach sein, ohne Konzepte von Automatisierung und Steuerung, aber der Versuch ist obligatorisch.
AntriebeAntriebe sind die Geräte, die die Motoren physisch speisen. Signale vom Achsbrett empfangen und in Motorleistung übersetzen.

 

[Fulvio Romano]

selettore di modeWie gesetzlich vorgeschrieben, haben Roboter immer einen Schlüssel-Hardware-Modus-Selektor. der Wähler hat hauptsächlich "automatische" und "manuelle" Funktionen, plus andere Zubehör, bequeme Funktionen, aber nicht explizit durch die Gesetzgebung erforderlich.
Automatischer Modus ist derjenige, in dem der Roboter seinen Arbeitszyklus unabhängig, ohne Überwachung durchführt. Es ist die klassische Arbeitsweise.
Der manuelle Modus ist der beim Programmieren verwendete. in dieser Phase muss der Programmierer tatsächlich die Möglichkeit haben, in der Nähe des Roboters sicher zu bleiben. in diesem Modus, um die Roboterarbeit zu machen, ist es notwendig, den Lehranhänger (siehe nach) in Hand zu haben, ist es möglich, mit einem Teil der umgangenen Schutze zu arbeiten, und die maximale Geschwindigkeit des Manipulators wird zur Sicherheit reduziert (geklemmt).

andere Modi können sein:
"100% manuell", in dem auch im manuellen Modus der Roboter mit maximaler Geschwindigkeit fahren kann. kann dies für eine begrenzte Zeitdauer tun und bestimmte Tasten gedrückt halten. Diese Funktion ist nützlich bei Aufgaben, die bei reduzierter Geschwindigkeit unterschiedliche Ergebnisse wie Malerei haben können.

Einige Roboter, die von einem externen Controller überwacht werden sollen, wie z.B. ein plc, müssen in einem bestimmten "supervisioned" Modus platziert werden, der aus Sicht der Gesetzgebung in allem zusammenfällt und für alles mit automatischem Modus.
SicherheitssicherheitIn Bezug auf die Sicherheit bieten Industrieroboter eine Karte mit bestimmten Eingängen. die aktuelle Gesetzgebung verpflichtet den Robotern eine Sicherheit der (Mindest-)Kategorie 3, das ist ein System, das bei einem (Einzel-)Versagen sicher bleibt, und dass es in der Lage ist, solche Fehler automatisch zu diagnostizieren (soweit möglich). Diese Sicherheit wird durch den sogenannten "Doppelkreis" oder zwei physikalisch getrennte Kanäle erreicht, die dieselbe Information bringen. bis die beiden Kanäle synchron bleiben, wird die Information als zuverlässig angesehen, wenn stattdessen die beiden Kanäle im Widerspruch stehen, hört das System auf und signalisiert einen Ausfall der Sicherheitskette.
ein ziemlich einfaches Beispiel kann ein Notfallpilz mit zwei Kontakten sein, die jeweils an der Robotersteuerung ankommen. wenn die beiden Kontakte geschlossen sind (nicht gepresst) ist der Roboter frei zu bedienen. wenn die beiden Kontakte öffnen (verklinkt) der Roboter stoppt. Wenn einer der beiden Kontakte scheitert, sieht der Controller die beiden Kanäle offen und einer geschlossen, versteht, dass es etwas falsch gibt, stoppt den Roboter und meldet den Fehler. zur Wiederherstellung des Fehlers ist es notwendig, die beiden Kontakte gleichzeitig zu öffnen und zu schließen, den Controller zu "demonstrate" das Problem gelöst zu haben. Wenn Sie dann beide Kabel schneiden, ist der Controller nicht in der Lage, den Ausfall zu diagnostizieren, aber in jedem Fall endet er in einem sicheren Zustand, weil es den Ausfall mit dem Pilzzustand verwirrt gedrückt. Deshalb müssen die Kontakte geöffnet werden. wenn es das Gegenteil wäre, würde der Controller im Falle des Schneidens der Kabel den Fehler mit "nicht gedrücktem Rauch" interpretieren und würde im unsicheren Zustand enden, im Gegensatz zu den Anforderungen der Kategorie 3 Sicherheit.

die Robotersteuerkarte genau das tut. nimmt eine Reihe von Sicherheitssignalen ein und entscheidet, ob die Motorleistung geschnitten werden soll. die Entscheidung erfolgt über Hardware, weil die Zuverlässigkeit größer ist als wenn sie über Software gemacht wurde.

zwei Arten von Notfall werden zur Verfügung gestellt. die sogenannte "Nothaltestelle" und "Autostop".
der Notanschlag, typischerweise, aber nicht notwendig, mit einem Pilz verbunden, schneidet die Leistung der Motoren unabhängig vom Zustand des Roboters. der automatische Stopp verhält sich stattdessen wie der Notfall nur, wenn der Roboter im "automatischen" Modus ist. Im "manuellen" Modus ignoriert der Roboter diese Art von Notfall. Es ist beispielsweise der Fall von Zutrittstüren zu einem abgegrenzten Bereich, wo der Programmierer den Roboter in manuellen sogar offenen Türen bedienen kann.

wie gesetzlich vorgeschrieben, wenn ein Stopp in Betrieb kommt, um den Roboter neu zu starten ist es notwendig, die Ursache des Notfalls zu entfernen (Löschen Sie den Pilz, schließen Sie die Zugriffe, etc.) und dann setzen Sie den Fehler freiwillig zurück.
Sonstigeandere Steuerelemente sind Leistungsanschlüsse, Eingangstransformator usw.

 

[Fulvio Romano]

lehren pendandt"Teach-Anhänger" ist der gemeinsame Name, mit dem auf die Programmiertastatur Bezug genommen wird. jeder Hersteller verwendet dann seinen eigenen Namen "flex pendant" oder "kcp" etc.
der Teachpendant dient der Programmierung des Roboters. Obwohl besonders komplexe Software häufig mit spezieller Software auf den PC geschrieben und getestet wird, ist der Teach-Anhänger jedoch für Veränderungen im Feld, für die manuelle Handhabung des Roboters, für die Betriebsprüfung von Programmen usw. unverzichtbar.

abhängig von der Kostrukturgestaltung kann sich stark ändern, aber im Prinzip besteht es aus folgenden Teilen:
Bildschirmder Teach-Anhänger entspricht einem Display, auf dem Sie den Programmcode sehen und zwischen den Menüs navigieren können. Einige Hersteller haben ein sehr komfortables und robustes Touchscreen-Display, speziell für die industrielle Umgebung.
Notfallnotfallder Teach-Anhänger hält immer an Bord eines Notpilzs. Dies wird durch die Rechtsvorschriften verhängt, die an jedem Arbeitsplatz einen Pilz verschreiben, und die tp stellt einen mobilen Arbeitsplatz dar.
Einige Hersteller haben den Schlüsselmodus-Auswahl oder lehren Anhänger. Leider hat es nicht jeder, während er extrem komfortabel ist, vor allem wenn die Arbeit in der Nähe des Roboters auf dem Feld und der Controller ist im Platz, vielleicht im oberen oder unteren Stock. wenn der Wähler auf dem Bild ist, Schalten aus dem automatischen Modus in manuell und umgekehrt bedeutet Treppen, Treppen und noch Treppen.
Joystick oder Bewegungstastender Roboter kann durch die Durchführung des Programms bewegt werden, aber offensichtlich muss es möglich sein, es auch manuell zu bewegen, um es in die gewünschte Position zu nehmen, und vielleicht dann im Programm solche Position aufzunehmen. dazu gibt es eine Reihe von Tasten, und sehr oft auch einen Jostick. Es gibt mehrere Bewegungsmodi, z.B. im Gelenkraum, dann "Bewegungsachse 1" oder "Bewegungsachse 2", oder im Arbeitsraum, z.B. "Langer Vorschub x", "Langer Anstieg z", etc. Sie wählen den Modus der Zeit bequemer.
Tastierawenn der Bildschirm nicht Touchscreen ist, hat der Teach-Anhänger eine echte qwerty-Tastatur. für diejenigen statt mit dem Touchscreen wird überwacht, und die physischen Tasten beschränken sich auf das "Spiel" des Programms, auf die "Stop", auf die "Pause", auf die Funktionstasten, etc.
nutzlos zu sagen, dass ich persönlich finde die mit dem Touchscreen viel bequemer.
Halte-zu-Laufist der wichtigste Knopf an Bord eines Flex-Anhängers. Wenn der Roboter im manuellen Modus bewegt wird, ist es von entscheidender Bedeutung, dass der Programmierer innerhalb der Risikozone des Roboters sein kann, bewusst bleibt und jederzeit sofort auf den Roboter eingreifen kann. während der Bewegung des Roboters, durch die Durchführung des Programms oder der Bewegung mit dem Joystick ist es notwendig, dass der Programmierer den Teach-Anhänger in der Hand hat, um den Roboter bei Bedarf ständig eingreifen und stoppen zu können. Er muss dann den Halt halten, um Knopf zu laufen (auch "tot man") in der Mitte seines Rennens. Wenn Sie den Teach-Anhänger legen, oder Sie es per Hand laufen, oder stolpern, oder schwach, wird der Halt zum Laufen Taste freigegeben und der Roboter stoppt sofort. wenn es angefärbt wird und die Tetanisierung der Muskeln der Hand machen es Vertrag, wird die Taste nach unten gedrückt, stoppen Sie den Roboter in jedem Fall.
Verbindung zum Controllerder Teach-Anhänger muss natürlich mit dem Controller verbunden sein. Typischerweise wird die Verbindung durch ein Ethernet-Kabel für das Display gebildet (was eigentlich ein kleiner indusrial pc ist), und eine Reihe von Cordern für den Notfallpilz, den Modal Selektor usw.
Es gibt nur einen Fall eines bekannten italienischen Roboterherstellers, der einen Teach Anhänger Wireless bietet. Es gibt diejenigen, die gut sprechen, und diejenigen, die schlecht sprechen. Sicher ist es unleugbar den Komfort, nicht Kabel zwischen den Füßen zu haben, die mit Staub verdrehen und füllen, aber es muss auch negative Aspekte berücksichtigen. vor allem das Gewicht. Arbeit für Stunden mit einem Teach-Anhänger, die doppelt so viel wie ein verkabelt Ich versichere Ihnen, dass auch Schulter und Ellbogen macht. und dann werden die Batterien entladen und wieder aufgeladen. Natürlich, die Batterien letzte 8h (bei Kauf!), d.h. eine Drehung, und dann gibt es die Ersatzpackung. Kamerabatterien dauern noch mehr, aber wie oft haben Sie sie Entladungen gefunden, wenn Sie sie brauchten? und in diesem Fall, wenn Sie die Batterien herunterladen, der Notfallpilz ist praktisch "premute", Stoppen des Roboters.

 

[Fulvio Romano]

KalibrierungIn Post #66 habe ich das Konzept der "Kalibrierung" eines Roboters vorgestellt und gesagt, dass es in Wirklichkeit drei Arten von Kalibrierungen gibt. die drei Typen haben tatsächlich verschiedene Zwecke und sie tun anders.
Fälschungenist die einfachste Kalibrierung, die normalerweise mehrmals während der Lebensdauer des Roboters durchgeführt wird, auch nicht durch Beschädigungen. Wie oben erwähnt, weisen die Gelenke sehr hohe Reduktionsverhältnisse auf, so dass auch für einige Stufen der Kupplung, des Motors und damit der Encoder/Resolver mehrere Windungen machen kann. um die Position des Gelenks zu kennen, ist es daher nicht nur erforderlich, die Position innerhalb der Runde, mit dem Encoder oder dem Resolver zu kennen, sondern auch die Anzahl der Windungen in der einen oder anderen Weise zu berücksichtigen. der Roboter verfügt über eine spezielle elektronische Karte, deren Aufgabe es ist, die Anzahl der Windungen jedes Motors genau zu erfassen und zu speichern.
Manchmal kann es jedoch vorkommen, dass der Roboter einen Treffer bekommt oder durch externe Kräfte mit übermäßiger Geschwindigkeit geschleppt wird, oder wenn er vom Controller getrennt wird oder der Controller ausgeschaltet ist. In diesen Fällen ist die Steuerung "die Kenntnis der Position des Manipulators nicht mehr ausreichend genau. dann, um zu vermeiden, dass sich der Roboter auf falschen Positionen bewegt oder sogar an den mechanischen Enden abstürzt, verliert der Controller die Zähler.
an dieser Stelle kann sich der Roboter nicht mehr bewegen, wenn nicht manuell mit niedriger Geschwindigkeit. muss erkannt werden.
so ist es genug, den Manipulator "zur Ferse" oder mit allen Gelenken auf Null zu bringen. Es ist keine große Präzision erforderlich, weil es ausreicht, dass das Gelenk auf dem "Null-Spin" liegt, aber es ist nicht notwendig, dass es tatsächlich im Nullwinkel ist, wie in der Runde der Winkel jedoch bekannt ist.
je nach Art des Roboters gibt es verschiedene Techniken, um es in Fersen einzusetzen. Einige Bauherren verwenden einfache Ziele, andere für Taktgeber. In jedem Fall, nach dem Ankleben des Manipulators, geben Sie einen Befehl des Zählerrücksetzens, und der Roboter ist wieder verwendbar.
Kalibrierung von GelenkenDiese Art der Kalibrierung wird erforderlich, wenn sie ersetzt wird, oder aber einen Motor, einen Reduzierer, einen Resolver usw. zerlegt wird, d.h. wenn die Referenz des Koppelwinkels (und nicht nur die aktuelle Runde) verloren geht. dies zu tun sind notwendige externe Geräte, da eine größere Genauigkeit erforderlich ist als die Kalibrierung am vorherigen Punkt. eine der Methoden ist die folgende. Bei manchen Robotern ist an jedem Arm eine maschinenbearbeitete Steigung ausgebildet, deren Ebene in enger Toleranz mit der Bezugsebene des Arms selbst steht, beispielsweise die Passage für die Achsen der Gelenke an ihren Enden. Es wird ein Differenzinkometer verwendet, d.h. eine Maschine aus zwei Inklinometern, die den Winkel zwischen ihnen zurückgibt. beide auf der Steigung des Lenkers 0, d.h. der Basis des Roboters liegen, und das Nullen des Differentials erfolgt. dann wird einer der beiden auf der Steigung des Lenkers 1 getragen und das Gelenk bis zu den Inlineometermarken 0 gedreht, an dieser Stelle der Resolver der Achse 1. und so auf feinkalibrieren alle Achsen.
am Ende dieses Verfahrens wird zusätzlich zu den Zählern die "Null" des Resolvers oder dem System mitgeteilt, was der Winkel ist, der als Null betrachtet werden muss. Diese Kalibrierparameter werden dann in einer Datei innerhalb des Controllers gespeichert.
andere Kalibriertechniken sehen die Verwendung von Tastatoren, die an bestimmten Stellen an den Armen angebracht sind. den "freien" Tastator der Kalibriertaschen, die die zuvor gesehenen Arbeitsteilungen ersetzen. unter Verwendung eines Taktgebers und eines automatischen Verfahrens sucht der Roboter nach Notch und Auto-Resets.
Obwohl diese Methode einfacher erscheint, gibt es mindestens zwei Kontraindikationen. das erste ist, dass der Zähler, wie er realisiert wird, eine Genauigkeit weniger als die des Inlineometers aufweist. das zweite, viel wichtiger ist, dass in diesem Fall die Azeration jedes Gelenks zwischen dem ihm vorgeschalteten Arm und dem darauf folgenden, den Fehler der Messung ansammeln. Bei Verwendung des Differential-Inline-Meters wird stattdessen jeder Arm mit der Basis des Roboters verglichen, das Ausmaß des Fehlers bleibt entlang der Struktur des Manipulators stabil.
Manipulator Kalibrierungdie Kalibrierung des Manipulators erfolgt in der Regel einmalig nur im Leben des Roboters. wird in der Fabrik gemacht, und in der Theorie muss es wiederholt werden, wenn die Fusion eines Arms ersetzt wird, was ziemlich selten ist.
Zweck dieser Kalibrierung ist es, die Parameter der Arme zu erhalten. nach der Vorstellung von Denavit-hartenberg (die ich im nächsten Beitrag erklären werde) hat jeder Arm vier unabhängige Parameter, von denen drei Konstanten und eine Variable. Wird die Größe nach dem eingangs beschriebenen Verfahren kalibriert, so müssen die drei konstanten Parameter mit einer bestimmten Technik ermittelt werden.
zur Durchführung dieser Art der Kalibrierung ist es erforderlich, den Roboter eines spitz zustellbaren Werkzeugs auszurüsten, d.h. dessen Position im Raum (z.B. dimensional) mit einer Auflösung von mindestens einer Größenordnung größer als diejenige, die für den Roboter realisiert werden soll. Es gibt mehrere Methoden zur Identifizierung im Raum dieses Werkzeuges, von der Verwendung von Kameras und bestimmten Zielen auf dem Werkzeug, bis zur Verwendung von realen Theodolyten, optisch oder elektronisch.

18 Positionen derart angeordnet, dass die Wirkung eines Parameters durch andere Parameter "verhitzt" wird. zu verstehen, wenn ich alle Positionen erhalte, die die Bewegung des Gelenks n nicht erfordern, wird die Identifizierung der Parameter der an dieses Gelenk angrenzenden Arme unmöglich oder zumindest nicht genau sein.
Tatsächlich werden viele mehr als 18 Positionen erfasst, es entsteht ein System von übergeordneten Gleichungen, das auf den Mindestquadraten aufgelöst wird.

 

[Fulvio Romano]

Alles klar?
Keiner stellt Fragen? Sind sie extrem klar oder extrem langweilig?
:smile:

 

[Exatem]

Alles klar?
Keiner stellt Fragen? Sind sie extrem klar oder extrem langweilig?
:smile:

langweilig klar oder klar langweilig??? :biggrin:
Ich mache nur Witze.
Weiter. oft lohnt sich die "silente Stille".
Ich sage Ihnen, warum oben und unten... Ich fragte mich oft, ob ich allein rede.
dann die Zahl der Besuche der Diskussion zu sehen, scheint es klar, dass viele lesen, ohne Fragen zu stellen.
Sie schreiben jedoch nicht, etwas zu beweisen, sondern, für die Leidenschaft in dem, was Sie tun (zumindest für mich ist es so und ich glaube auch für Sie).
Ich erneuere Ihre Komplimente öffentlich für Ihre Exposition.

 

[PierArg]

langweilig klar oder klar langweilig??? :biggrin:
Ich mache nur Witze.
Weiter. oft lohnt sich die "silente Stille".
Ich sage Ihnen, warum oben und unten... Ich fragte mich oft, ob ich allein rede.
dann die Zahl der Besuche der Diskussion zu sehen, scheint es klar, dass viele lesen, ohne Fragen zu stellen.
Sie schreiben jedoch nicht, etwas zu beweisen, sondern, für die Leidenschaft in dem, was Sie tun (zumindest für mich ist es so und ich glaube auch für Sie).
Ich erneuere Ihre Komplimente öffentlich für Ihre Exposition.

auch weil Ich habe die "Brauen" bereits mit meinen Fragen gebrochen.:biggrin:

 

[Fulvio Romano]

Es wird nicht leicht sein, über dieses Thema zu sprechen. Ich möchte den Saft der Materie beschreiben können, ohne mich in mathematischen Details zu verlieren. Natürlich, wenn jemand interessiert sein muss, müssen Sie nur fragen.

Ziel dieser Diskussion ist es, die Kinematik eines Manipulators rechnerisch einfach zu beschreiben. in der Praxis wollen Sie sich vom Gelenkraum in den Arbeitsraum (direkte Kinematik) und umgekehrt (inverse Kinematik) bewegen. Der geometrische Ansatz, wie wir sehen werden, ist weder einfach noch mathematisch robust, aber in jedem Fall ist das erste Problem, mit dem wir umzugehen, eine Notation für die Beschreibung der Kinos zu etablieren.

jacques denavit und richard scheunemann hartenberg konfrontiert und löste erstmals auf organische und strukturierte Weise eine Methode zur Behandlung offener und geschlossener Kinoketten, aber ohne mehrere Links. Außerdem arbeitet diese Methode nur bei Dreh- oder Prismengelenken.
Das erste, was zu tun ist, den verschiedenen Armen feste Referenzrahmen zuzuordnen. Obwohl theoretisch möglich ist, diese in irgendeiner Weise orientierten Rahmen zuzuordnen, können Sie mit der Notation von Denavit-hartenberg Terne auf einzigartige Weise etablieren und die nächsten Schritte automatisieren.

- Gelenkachsen identifizieren und nummerieren, deren Richtungen z0, zn sind;
- wählen Sie eine Basis terna [X0, Y0, Z0] fixiert;
- wählen Sie zi giacent entlang der Achse des Gelenks i+1
(ii) der Ursprung des i-ten Terna, der Schnittpunkt von zi mit der normalen Gemeinde (in einem minimalen Abstand) zur Achse zi-1 und zi. wenn die Achsen parallel sind und die Achsen rotieren, positionieren oder d(i) abbrechen (siehe später das, was d(i) ist), während sie prismatisch ist, wählen oder in Übereinstimmung mit einer Referenz des Gelenkhubs, beispielsweise eines Endlaufs;
- wir nennen die Kreuzung der normalen Gemeinde mit zi-1
- die direkte Achsenachse entlang der normalen gemeinsamen Achse zi-1 und zi mit positiver Richtung vom Gelenk i+1 zu fixieren;
- die yi-Achse muss gewählt werden, um eine Levogira terna zu vervollständigen.

und wenn der Mindestabstand nicht definiert ist?
- wenn die Achsen parallel sind, kann der Punkt oi an einer Stelle zur Bitte genommen werden.
- wenn die Achsen Unfälle sind, wird der Punkt am Schnittpunkt gewählt.

Die zweite Sache ist, die sogenannte "denavit-hartenberg-Tabelle" zu kompilieren, d.h. für jeden Link müssen folgende Parameter kompiliert werden:
- Ja. a(i), oder Linklänge: Abstand zwischen oi und o'i.
- Ja. d(i), oder gemeinsame Entfernung: koordiniert von o'i auf zi-1
- Ja. alpha(i), oder Link Drehung: Winkel zwischen zi-1 und zi um xi
- Ja. Tante!, oder Winkel des Gelenks: Winkel zwischen xi-1 und xi-Achse um die zi-1 Achse. bei Drehgelenk ist dieser Winkel die Gelenkgröße.

Sobald die vier Parameter für jeden Link gewonnen werden, ist die Struktur vollständig charakterisiert. Ich werde keine Matrizen schreiben, aber es ist leicht zu erraten, dass ich das terna i mit dem terna i+1 überlappen muss ich translarla von "d" und "a" und drehen es von "teta" und "alpha". Es ist daher möglich, vier Matrizen, zwei Übersetzungen und zwei Rotationen zu schreiben. unter ihnen diese vier Matrizen zu multiplizieren wird eine Matrix zu(i)(i+1) der Rotation erhalten, die es erlaubt, sich vom Gelenk i+1 zu bewegen. an dieser Stelle verstehen Sie den Vorteil der Notation von Denavit-hartenberg. In der Tat hat die Matrix eine feste Struktur, die für jeden Kinoismus bekannt ist. Es ist daher nicht notwendig, sie jedes Mal zu erhalten.

aus der betrieblichen Sicht also, wenn Sie den Tisch von denavit-hartenberg bemerken, Sie nur "zusammen" die verschiedenen Matrizen a.

Durch Multiplizieren der verschiedenen Matrizen zueinander ergibt sich eine Gesamtmatrix des gesamten Manipulators, die die Orientierung des Werkzeugs terna gegenüber der Basisterna beschreibt. Was brauche ich? Stellen wir uns vor, dass der Manipulator "in Hand" ein Objekt hat. Diese Aufgabe wird durch Koordinaten bezüglich des Endorgans identifiziert, fixiert, weil das Objekt solidarisch mit dem Endorgan ist. Wenn ich diese Koordinaten für die Matrix t multipliziere, bekomme ich die Koordinaten des Objekts im Vergleich zur Basis Terna, also zur Welt.

Hier wird also das Problem der Direktkinetik gelöst, d.h. die Gelenkwinkel in die Matrix t einfügen und ich bekomme die Position des Werkzeugs in Bezug auf die Basis.

 

[Fulvio Romano]

Ganz im Gegenteil, direkte Kinofilme sind keine großen Probleme. und wenn die Denavit-hartenberg-Methodik einen sicheren Weg bietet, auf dem Sie sich bewegen können, können Sie immer noch verschiedene Ansätze verwenden, insbesondere für einfache Geometrien, um das Problem zu lösen.
Es ist nicht so für umgekehrte Kinos. die Matrix t ist eine äußerst komplexe trigonometrische Matrix. Es ist daher nicht interessant, die Funktion umzukehren:

x = t(q)

wobei q = (q1, q2, ..., qn) der Vektor der Gelenkvariablen ist und x = [p, fi] = [(x1, x2, x3), fi) è il vettore posa (= posizione + orientamento) nello spazio operativo. Perché non esplicito il vettore orientamento fi? Beh...lo vedremo tra un po', non è così ovvio.

Dunque, se l'equazione scritta sopra è quella che descrive la cinematica diretta, la cinematica inversa può essere scritta così:

q = k(x)

E' un'equazione estremamente complessa, fortemente non lineare, può ammettere soluzioni multiple in talune situazioni, in altre non esistono soluzioni ammissibili. Sebbene quindi in alcuni casi possa risultare intuitiva, essa NON viene ricavata in forma chiusa se non per strutture estremamente semplici, come i manipolatori planari a più bracci.

DifferentialkinematikSehen wir sofort etwas. Wenn ich ein prismatisches Gelenk mit x-Geschwindigkeit habe, bewegt sich sein Ende mit x-Geschwindigkeit. Wenn es sich auf 2x bewegt, bewegt sich das Ende auf 2x. Wenn ich stattdessen ein Drehgelenk habe, das mit der Winkelgeschwindigkeit w rotiert, bewegt sich das Ende mit der Geschwindigkeit w*r. Wenn es auf 2w dreht, bewegt sich das Ende auf 2w*r. Es scheint offensichtlich, aber so einfach ist es der Schlüssel zu Differentialkinetik.
wir wollen die Position des Werkzeugs nach den gemeinsamen Variablen finden, aber wenn wir direkt nach dieser Position suchen, kommen nichtlineare, instabile und komplexe Gleichungen heraus. Wir haben gerade gesehen, dass, wenn wir statt Position die Aufmerksamkeit auf Geschwindigkeiten beheben, das Problem plötzlich linear wird.

dann entscheiden, eine neue Matrix zu schreiben. da diese Matrix Geschwindigkeitsraten enthalten wird, d.h. die Ableitung dessen, was wir wirklich interessieren, d.h. die Position, werden wir es nennen "Jacobiano". wir suchen daher nach einer solchen Matrix, so dass es möglich ist, eine solche Gleichung zu schreiben:

x’ = j(q) * q’

x' = [p', w] ist der Geschwindigkeitsvektor (Geschwindigkeit und Winkelgeschwindigkeit) und j ist der Jacobiano (geometrische). das Symbol <'> die Ableitung der Variablen/Vektorzeit darstellt. Tut mir leid, aber hier auf dem Forum kann ich den Punkt nicht über den Brief setzen..

Durch das Lesen der oben geschriebenen Gleichung verstehen wir, dass jedes Element der Matrix j den Beitrag eines Gelenks darstellt. Wenn wir die mütterliche Entwicklung zum Ausdruck bringen, erhalten wir:

== sync, korrigiert von elderman ==
vy = j21*q1 + j22*q2 + j2n*qn
...

aber wie man einzelne Jab-Elemente schreibt?

Ich schreibe keine Formeln, die ich auf Anfrage veröffentlichen werde, aber das Konzept ist wie folgt:

für eine Prismengelenk jede Gelenke die folgenden Beiträge und damit die entsprechende Jab:
- die Winkelgeschwindigkeit eines Gelenks gegenüber dem vorherigen bleibt gleich;
- die Lineargeschwindigkeit eines Gelenks gegenüber dem vorherigen wird in Richtung der Gelenkachse erhöht.

für eine Drehgelenk anstatt:
- die Winkelgeschwindigkeit eines Gelenks im Vergleich zu den vorherigen Zunahmen von q';
- die lineare Geschwindigkeit eines Gelenks gegenüber dem vorherigen erhöht q' für die Länge des Arms.

die hier geschriebenen Aktien sind relativ zu jedem Gelenk gegenüber dem vorherigen. die direkte filmische Matrix t(q), die wir sahen, bevor es möglich ist, alle diese Elemente wieder an das Terminalorgan zu bringen.
Letztlich haben wir eine j(q)-Matrix mit den verschiedenen Verbindungsraten zu den verschiedenen Geschwindigkeitskomponenten im Betriebsraum gebaut, die im Vergleich zum Endorgan geschrieben wurden.

Gut, aber wir waren an der Position interessiert und nicht an der Geschwindigkeit... also?

 

[Fulvio Romano]

Wir sagen sofort, dass die Tatsache, Differentialkinetik in linearer Form zu schreiben, nicht bedeutet, dass seine Inversion in geschlossener Formel durchgeführt wird. Auch in der Tat ist das Konzept, eine Formel zu haben, Berechnungen zu machen und ein Ergebnis zu erhalten, nicht zu gewinnen. Es gibt sehr robuste und wenig schwere Techniken aus der rechnerischen Sicht.

wir sehen einen interessanten Algorithmus, der auf der Rückseite des jacobiano basiert.
die Formel zu "invert" ist:

♪

Deshalb können wir links beide Mitglieder für die Rückseite von j multiplizieren:

♪

Grundsätzlich ist es möglich, einen Algorithmus zu schreiben, der ausgehend von der aktuellen Position des Manipulators j(q) rückgängig macht, durch x’ multipliziert und q’ erhält.
scheint zu funktionieren, aber es gibt ein Problem. in jedem Schritt des Algorithmus wird der q-Vektor des vorherigen Schrittes und der x-Vektor des aktuellen verwendet. Diese Inkonsistenz führt zu einem Fehler, der lange zu gehen kann eine numerische Drift beginnen und im Regime sinnvoll werden.

um dieses Problem zu überwinden, wird ein anderer Algorithmus angenommen. Zuerst definieren wir den Fehler als Differenz zwischen der gewünschten Position und dem aktuellen:

e = xd – x

aus der Zeit:

e’ = xd’ – x „

Ziel des Algorithmus ist es, den Fehler, zumindest zu Regimen, auf Null zu bringen.

Nehmen Sie an, die folgende Gleichung zu schreiben:

(xd' + k*e)

das, was wir zuvor geschrieben haben, die folgende Gleichung ergibt sich:

= 0

Es bedeutet, dass die Evolution in der Fehlerzeit so ist, dass sie im Regime abbricht, selbstverständlich, wenn die k-Matrix positiv definiert ist, beispielsweise eine Diagonalmatrix.
also, wenn wir einen Algorithmus auf Basis dieser Formel verwenden, vermeiden wir eine Drift von Fehlern und sorgen für asymmetrische Stabilität.

ein Blockschema, das die Implementierung dieses Algorithmus darstellt, ist in der Figur dargestellt. Diese Arten von Systemen sind sehr vertraut denen, die bazzica matlab und simulink, wir versuchen, es zu erklären.

ist nichts anderes als eine grafische Darstellung eines zyklischen Algorithmus. während eines Schrittes der Ausführung, haben wir die xd Größe, das ist der "Set-Punkt", den Verlegewert, den wir wollen, dass der Manipulator zu erreichen. dazu gehen wir, die aktuelle Pose zu entfernen. Dies wird berechnet, indem die Kopplungsvariablen des vorherigen Schrittes (siehe Pfeil "gegen Strom") und durch direkte Kinematik (d.h. durch Multiplikation der Matrix t) die Stromverlegung berechnet wird.
nachdem der Summiererknoten xd - x = und, die Differenz zwischen der Soll-Position und der Ist-Position, das ist der Fehler.
Fehler (der Fehlervektor) wird mit einer k-Matrix multipliziert. Variation der Werte dieser Matrix können Sie das Verhalten des Algorithmus ändern.
dann haben wir den Wert "k*e", der zusammen mit x'd den Summenknoten eingibt, oder die gewünschte Geschwindigkeit. Diese Größe kann einfach über die Zeit von der gewünschten xd-Position abgeleitet werden.
erneut durch die Rückseite des Jacobiano multiplizieren wir endlich die folgende Formel:

♪

Das war die Grundlage des Algorithmus. Wir integrieren das, das heißt, wir setzen es auf das Ergebnis der vorherigen Schritte, und wir bekommen q.

Ich bin fertig. ohne jede Formel umkehren zu müssen, mit einem einfachen wiederkehrenden Algorithmus konnten wir q von xd erhalten, d.h. Wir haben die Reverse-Kinotik gelöst!Dieser q-Wert wird mit direkter Kinematik (Matrix t) verwendet, um das zuzuführende x zum nächsten Zyklus des Algorithmus zu berechnen und auch den Wert von j(q) zu berechnen, der, wie wir gesehen haben, Funktion von q ist.

Leute, ich schwöre, ich habe nur die streng unverzichtbare Mathematik benutzt. Aber es war ein kleines Detail wert, oder?
Diese Methoden der Filterung konvergenter Algorithmen werden in sehr wenigen Fakultäten untersucht, aber, sobald sie gut verstanden sind, sind sie ein grimaldello, die verwendet werden können, um Probleme sonst kompromisslos zu lösen. Ich würde diese Themen unmittelbar nach der Analyse ii studieren und für alle technischen Adressen verbindlich machen.

 

[maxopus]

Hola fulvio, ich muss Zeit finden, um ruhig Ihre letzten Beiträge zu lesen.

es scheint alles sehr schön

 

[PierArg]

... Ich muss Zeit finden, um Ihre letzten Beiträge ruhig zu lesen.

...

auch, weil er uns schlecht gab: Großgrin::Tochter:

 

[Marcos555]

Ruhe ein bisschen mit all diesen Beiträgen.

Schreiben Sie einen schönen Text von Robotik-Elementen oder Mechatronik und machen Sie es frei, für die Benutzer des Forums, das interessiert mich.

 

[africagia]

Mir gefällt es. wie pier sagt: Geben Sie uns in schlecht! :biggrin:

Leute, ich schwöre, ich habe nur die streng unverzichtbare Mathematik benutzt. Aber es war ein kleines Detail wert, oder?

Natürlich, weiter!

Diese Methoden der Filterung konvergenter Algorithmen werden in sehr wenigen Fakultäten untersucht, aber, sobald sie gut verstanden sind, sind sie ein grimaldello, dass
kann verwendet werden, um Probleme sonst unsicher zu lösen. Ich würde diese Themen unmittelbar nach der Analyse ii studieren und sie verpflichtend machen
für alle technischen Adressen.

wäre eine gute Idee, einen fortgeschrittenen Inspektionskurs für alle technischen Adressen zu tun. selbst wenn meiner Meinung nach das übliche Problem bleibt
der italienischen Universität: so viel Theorie, aber wenig Praxis. Vielleicht kann in Zukunft mit der Erfahrung auf dem Gebiet ein Vorteil sein. Vielleicht. Zum Beispiel für mich,
Weil ich diese Dinge noch nicht gesehen habe, ist etwas nicht so klar. Angenommen ich habe meinen schönen Roboter und ich wollte
implementieren Sie den jacobiano Reverse-Algorithmus, den Sie gezeigt haben. Wie mache ich das? wie übersetze ich das Blockdiagramm (oder viele andere, die ich studierte) praktisch? Ich bin immer noch unklar, wie ich sie wirklich erreichen kann.

 

[Fulvio Romano]

Angenommen ich habe meinen schönen Roboter und ich wollte
implementieren Sie den jacobiano Reverse-Algorithmus, den Sie gezeigt haben. Wie mache ich das? wie übersetze ich das Blockdiagramm (oder viele andere, die ich studierte) praktisch? Ich bin immer noch unklar, wie ich sie wirklich erreichen kann.

qui die Beschreibung des Controllers finden.
der Controller beherbergt einen industriellen PC, der sich mit diesen Problemen befasst, die "zentralen" genannt werden, weil sie eine globale Analyse aller Gelenke erfordern.
auf dem pc ist ein Echtzeit-Betriebssystem installiert (= deterministisch), typischerweise Linux, qnx, vxworks, etc., und dreht eine Steuersoftware. die Steuersoftware, ist für die Erstellung des obigen Algorithmus verantwortlich, d.h.:
- nimmt Informationen vom Achslenker
- führt einen Zyklus
- erzeugt Sollwerte für die Achssteuerung.

der Zyklus kann ähnlich dem unten in Metacode geschriebenen sein:

Start

weiterlesen <posizione desiderata=""> von <pianificatore di="" traiettorie="">weiterlesen <giunti attuali=""> von <scheda seriale="">berechnet <velocità desiderata=""> durch <derivazione> von <posizione desiderata="">berechnet <posizione attuale=""> durch <cinematica diretta=""> von <giunti attuali="">berechnet <jacobiano> durch <struttura jacobianto=""> von <giunti attuali="">und <posizione desiderata=""> - Ja. <posizione attuale=""><temp> = k * und + <velocità desiderata=""><setpoint ai="" giunti="" velocità=""> ♪ <temp> * <jacobiano><setpoint giunti="" posizione=""> ♪ <setpoint giunti="" posizione=""> + <setpoint ai="" giunti="" velocità="">Schreiben <setpoint giunti="" posizione=""> auf <scheda assi.="" controllo="">zurück zum Anfang</scheda></setpoint></setpoint></setpoint></setpoint></jacobiano></temp></setpoint></velocità></temp></posizione></posizione></giunti></struttura></jacobiano></giunti></cinematica></posizione></posizione></derivazione></velocità></scheda></giunti></pianificatore></posizione>

 

[africagia]

Okay. Das auf hohem Niveau. Aber wenn der Controller wollte, dass ich es tue? Ich werde es erklären. Angenommen, wir haben nur n (Annahme n = 6) Glieder, die miteinander mit rotierenden oder prismatischen Paaren verbunden sind. Angenommen, ich habe alle Sensoren, die ich brauche, usw. Ich habe mein Kontrollrecht entschieden. Wie erkenne ich es auf niedrigem Niveau? d.h. wie mache ich es elektronisch (oder analog oder digital)? die Begründung, die ich tue, ist die folgende. in siso Systemen (sowohl analog als auch digital) Ich habe ein System, das ich in der Retroaktion steuern will, ich berechnen meine Übertragungsfunktion (oder mit laplace oder z-transformiert), die mir erlaubt, das System wie ich will zu steuern, dann gehe ich zur Realisierung einer Schaltung (oder mit analogen Komponenten oder mit einem Mikro), die die gleiche Übertragungsfunktion hat, die ich gewählt und ich gehe, um es in der Regelschleife zu platzieren, bevor mein System zu steuern. im Falle unseres Roboters (mit nur 6 armen Eisenstücken, die miteinander verbunden sind), was noch ein System ist (obwohl mimo), wie kann ich das alles realisieren?

 

[Fulvio Romano]

Okay. Das auf hohem Niveau. Aber wenn der Controller wollte, dass ich es tue? Ich werde es erklären. Angenommen, wir haben nur n (Annahme n = 6) Glieder, die miteinander mit rotierenden oder prismatischen Paaren verbunden sind. Angenommen, ich habe alle Sensoren, die ich brauche, usw. Ich habe mein Kontrollrecht entschieden. Wie erkenne ich es auf niedrigem Niveau? d.h. wie mache ich es elektronisch (oder analog oder digital)? die Begründung, die ich tue, ist die folgende. in siso Systemen (sowohl analog als auch digital) Ich habe ein System, das ich in der Retroaktion steuern will, ich berechnen meine Übertragungsfunktion (oder mit laplace oder z-transformiert), die mir erlaubt, das System wie ich will zu steuern, dann gehe ich zur Realisierung einer Schaltung (oder mit analogen Komponenten oder mit einem Mikro), die die gleiche Übertragungsfunktion hat, die ich gewählt und ich gehe, um es in der Regelschleife zu platzieren, bevor mein System zu steuern. im Falle unseres Roboters (mit nur 6 armen Eisenstücken, die miteinander verbunden sind), was noch ein System ist (obwohl mimo), wie kann ich das alles realisieren?

Ich muss noch nicht kontrollieren. Wir sind in der Kinoschau angekommen, wir müssen immer noch über direkte Dynamik, Umkehrdynamik, unabhängige Steuerungen zu den Gelenken sprechen, zentralisiert.... wir bereiten Analysen ii vor und wir kamen in die Algebra...:Ziege:

die Architektur des Controllers ist die oben beschriebene. als Kommandoorgane von dort nicht entkommen, auch weil es mehr oder weniger Standardarchitektur für die gesamte Welt der Bewegungssteuerung ist.

der Algorithmus der filmischen Inversion "absolute" zu einer Kontrolle in der Retroaktion, nicht umsonst, weil es aus dem Geist der Kontrollen geboren wurde. aber es ist keine Kontrolle. in einem Steuerungssystem gibt es ein System zur Steuerung und einen Controller, der Referenzen generiert, hier haben wir nichts zu kontrollieren, aber nur einen Algorithmus zu konvergieren.

Da Sie über Transformation reden, versuchen wir, in ein wenig mathematischeres Detail zu kommen. Ich schlage vor, dass wir in der Theorie laplace verwenden können, um das Modell zu vereinfachen und seine Stabilität zu analysieren, aber richtiger würde es immer zeta verwendet werden, weil wir immer mit digitalen Steuerungen zu tun haben, und daher zu einer diskreten Zeit.

Das sagte, ich warf dort ein ziemlich tiefes Konzept, aber ohne es zu sehen. als ich über k sprach, das ist der Multiplikator des Fehlers, sagte ich, es muss eine "positive definierte Matrix" sein. Warum?

Insbesondere brauche ich positive reale Werte, weil aus energiepolitischer Sicht die asymmetrische Stabilität des Algorithmus als Gleichgewichtsfrage betrachtet werden kann. Wir sagten, dass der primäre Zweck der Wahl dieses Algorithmus ist, eine differentielle Gleichung der Evolution des Fehlers im Raum der Zeit zu repräsentieren, die nichts im Regime ist.
Wie Sie sehen können, spreche ich nicht von Polen und Nullen, nur weil wir nicht über ein System der Kontrolle reden, sondern einfach einen evolutionären Algorithmus. die Schönheit dieses Algorithmus ist, dass, wenn es aus der Energiesicht dargestellt ist, muss es dem Theorem von lyapunov gehorchen.
die evolutionäre Funktion des Fehlers ist genau eine Kandidatfunktion von lyapunov und ist k eine konstante und definierte positive Matrix, die Balance ist global attraktiv.

An dieser Stelle sage ich Ihnen auch den Algorithmus mit dem transponierten jacobiano, der noch interessanter ist mathematisch, obwohl es niedrigere Leistungen hat.

 

[Fulvio Romano]

versuchen wir, diesen anderen Algorithmus zu sehen. Ich hatte beschlossen, ihn zu verlassen, aber da jemand interessiert ist, lass uns sehen, wie man ihn beschreibt.
die Verwendung der Rückseite der jacobiano funktioniert im Wesentlichen, weil die Rückseite der Matrix die algebraische Lösung der Inversion der Kinos ist. der vorher gesehene Algorithmus ist eine Methode, um die Konvergenz einer wiederkehrenden Zählung zu gewährleisten.

Stattdessen sehen wir einen einfacheren Algorithmus aus der rechnerischen Sicht, weil er die Umsetzung des Jacobianos ausnutzt. Es geht darum, eine Verbindung zwischen der Geschwindigkeit zu den Gelenken und dem Fehler zu finden, daß die Nullkonvergenz dieser keine Linearisierung erfordert. wie erwähnt, wird die Stabilität des Algorithmus durch das Theorem von lyapunov gewährleistet. Wir wählen eine quadratische Form als Kandidatenfunktion von lyapunov, die eine Art Potential im Raum des Fehlers definiert erinnert:

v(e) = 1/2 und (übersetzt) k und

wobei k eine symmetrische und definierte positive Matrix, beispielsweise Diagonal, ist. differenziert von der Zeit und erinnert daran, dass x' = j(q) q' erhalten wird:

v' = e(transponiert) k xd' - e(transponiert) k j(q) q'

Also, wenn wir wählen

q' = j(transponiert) k und

wir

v' = e(transposed) k xd' - e(transposed) k j(transposed) k und

Ist die Geschwindigkeitsreferenz konstant, so wird xd' = 0, v' negativ definiert, während v positiv definiert wurde, dann ist für den Lyapunov das System asymptotisch stabil.
Sollte stattdessen xd' von Null verschieden sein, kann nichts über das Vorzeichen der ersten Term der vorherigen Gleichung gesagt werden, dann wäre das System grundsätzlich nicht asymptotisch stabil. wahr, aber der Fehler kann klein gehalten werden, die Norm von klein k., nicht null zu Regime, genau aus diesem Grund haben wir gesagt, dass der Algorithmus mit transponiert ist weniger Leistung als die mit umgekehrt.
unter anderem k kann nicht einmal auf Dismistress erhöht werden, weil der Algorithmus in diskreter Zeit umgesetzt wird und Sie die numerische Instabilität riskieren.

 

[Fulvio Romano]

Ich habe eine kurze Klammer in Mathe gemacht. Ich hoffe, ich habe den Leser nicht zu viel gefürchtet, aber ich würde zurückkommen, um die Argumente auf weniger strenge Weise zu behandeln, aber sicherlich intuitiver, die mathematische Formalität zu verlassen, dass, obwohl von lebenswichtiger Bedeutung für diejenigen, die diese Konzepte in der Praxis verwenden müssen, ist statt nur eine Reihe von langweiligen Buchstaben für diejenigen, die mit einem romanischen Geist zu lesen.
Die Forderung nach genaueren Klärungen bleibt jedoch offen für diejenigen, die Neugier haben.

Gehen wir zurück, um über den Jacobiano zu sprechen, denn selbst für diejenigen, die davon überzeugt sind, dass die Matrizen eine Art der Kleidung der Wäsche sind, kann intuitiv sein, was ich zu sagen habe.
wir haben gesagt, dass die jacobiano, j[q(t)] stellt die Verbindung zwischen Geschwindigkeit zu Gelenken und Geschwindigkeit im Arbeitsraum eines Manipulators dar. Diese Matrix ist voller Bedeutung und kondensiert sofort eine Vielzahl von Informationen über den Manipulator selbst und seine sofortige Konfiguration.
jacobiano als Anwendungjacobiano kann als eine "Anwendung" oder eine Art "Funktion" betrachtet werden, die nicht zu viele Ansprüche auf Domain und Codomain hat. Stellen wir uns zwei Sätze vor. das erste, q', ist das Set aller Geschwindigkeiten, die die Gelenke eines Manipulators haben können. wir stellen uns einen planaren Manipulator mit zwei Armen und zwei Gelenken vor, der ein Quadrat in r2 ist. entlang der Riots die q1' Geschwindigkeiten des ersten Gelenks entlang der geordneten q2' des zweiten Gelenks. jeder Punkt innerhalb dieses Quadrats stellt mit seinen Koordinaten ein paar Geschwindigkeit zu den Gelenken dar.
in einem anderen Raum, immer r2, wird es ein weiteres Quadrat, sicherlich mit unterschiedlicher Form, die stattdessen die Geschwindigkeiten des Klemmorgans im Operationsraum darstellt. jeder Punkt des rechten Quadrats ist das Bild eines Punktes des linken Quadrats durch das Jacobiano erhalten.
wir versuchen, diese Quadrate abzustrahieren, bis wir sechsdimensionale Hypercubes bekommen. Die Substanz der Materie ändert sich nicht, aber jetzt können wir beschreiben, was für einen Manipulator bei sechs Mobilitäts- und sechs Freiheitsgrade geschieht.
die jacobiana Matrix kann einen "null" oder einen Subraum der linken Figur haben, deren Bild in den "Null" Punkt der rechten fällt. in der Praxis eine auf die Gelenke eingestellte Geschwindigkeit, die keine Geschwindigkeit im Arbeitsraum beinhaltet. Stellen Sie sich einfach ein kugelförmiges Handgelenk in der Singularität des Handgelenks vor, das heißt mit den Achsen 4 und 6 ausgerichtet ist. Dreht sich die Achse 4 mit einer bestimmten Geschwindigkeit und 6 mit gleicher Geschwindigkeit in entgegengesetzter Richtung, so hat sie, daß das Endorgan fest bleibt. Dieser "Punkt" fällt dann sicher in die Leere des Jacobianos, die für den Anlass (Singularität) ist auch Singular... aber wir sehen es am nächsten Punkt. Wenn es sehr kompliziert ist, intuitiv zu erkennen, was die Geschwindigkeitssätze sind, die nichts im Betriebsraum beinhalten, ist es ziemlich einfach genug, die Theorie der matrischen Berechnung auszunutzen, die Leere des Jacobianos zu identifizieren. Diese Matrix sagt uns also mit strengem mathematischen Formalismus eine sehr interessante erste Sache über den Manipulator.
EinzigartigkeitWir sahen, was die Singularitäten sind. sind Positionen der Achsen eines Manipulators, von dem es nicht möglich ist, eine Verschiebung zum Vergnügen zu erhalten. z.B. im planaren Manipulator zu zwei Armen, wenn diese ausgerichtet sind, haben Sie eine Singularität; Für den Manipulator ist es unmöglich, eine Bewegung entlang der Arme zu machen, während er nur orthogonal zu ihnen bewegen kann.
ein anthropomorpher Manipulator hat zwei Arten von Singularität.
- die Schulter Singularität, wenn sich die Pulsmitte an einem beliebigen Punkt in der Achse 1 befindet; in der Tat kann sich der Manipulator nicht in orthogonaler Richtung auf der Ebene bewegen, die durch die ersten beiden Arme gebildet wird.
- die Handgelenk Singularity , wenn die Achsen 4 und 6 ausgerichtet sind, und wir sahen es vorher.

Was passiert mit dem Jakobian, wenn der Manipulator in Singularität ist? einfach, es absinkt von Rang, und daher seine Bestimmung ist null, und daher ist seine Umkehr nicht definiert, und daher immer noch seine Null-Größe (diese Dimensionen, wie viele Punkte den Rang gefallen hat).
Wieder einmal übersetzt eine kritische Situation des Manipulators in die mathematische Kritik des Jacobianos.

in der Schulter Singularität, wenn ich eine Drehung der Achse 1 habe, bleibt das Handgelenkzentrum fest. jacobiano informiert uns darüber, indem wir alle Achse eins auf Null des Geschwindigkeitsraums zu den Gelenken projizieren.
RedundanzWas passiert, wenn ich einen redundanten Manipulator habe? die jacobiano bezieht die Geschwindigkeiten im Gelenkraum und die im Arbeitsraum. Wenn aber der Manipulator redundant ist, bedeutet dies, dass die Anzahl der Gelenke (j Spalten) größer ist als die Anzahl der Abmessungen des Betriebsraums (j Zeilen), in dem es sich bewegen kann. Stellen Sie sich vor, ein Roboter mit sieben Gelenken (7 Grad der Mobilität und 6 Grad der Freiheit), aber auch ein planarer Manipulator mit vier Armen (4 Grad der Mobilität und 3 Grad der Freiheit im Plan). Welche Form nimmt der Jacobiano? einfach, es ist rechteckig, und das bedeutet verschiedene Dinge.
Erstens ist es nicht möglich, die Umkehr zu berechnen. Was bedeutet das aus physikalischer Sicht? wenn der Jacobin die Geschwindigkeit der Gelenke in der Tatsache projiziert, dass es rechteckig ist, und insbesondere nicht invertierbar, bedeutet, dass es bei strenger Wahl keine Lösung (univocal) des umgekehrten Kinos gibt. In der Praxis ist es bei einer im Betriebsraum eingestellten Geschwindigkeit nicht möglich, die daraus resultierenden Gelenke (univokativ) mit einer Geschwindigkeit zu identifizieren. In der Tat gibt es für redundante Manipulatoren unendliche Geschwindigkeitssätze an die Gelenke, um eine bestimmte Geschwindigkeit im Arbeitsraum zu erhalten (solange dies natürlich innerhalb des Bildes von j liegt).
zum Beispiel stellen wir uns einen vierarmigen Planarmanipulator vor und stellen uns vor, dass wir die Geschwindigkeit im Operationsraum v = [0, 0, 0], d.h. festes Endorgan. offensichtlich gibt es die triviale Lösung q'=[0, 0, 0, 0] mit allen noch gültigen Gelenken auch für nicht redundante Manipulatoren, aber der rechteckige Jacobiano 4x3 erinnert uns daran, dass es für diesen redundanten Manipulator möglich ist, interne Bewegungen an die Struktur zu haben, auch wenn das Klemmorgan fest ist. d.h. es gibt keine eindeutige Geschwindigkeit, um die Gelenke zu geben, so dass das Endorgan noch ist, aber es gibt unendliche.

Offensichtlich bedeutet die Nichtinvertibilität des Jacobin überhaupt nicht, dass das Problem der Umkehrkinetik unlösbar ist. Fügen Sie einfach einige zusätzliche Anleihen hinzu. nicht innerhalb der Details, sondern es ist beispielsweise möglich, Zwänge einzuführen, so dass der Manipulator mit den Armen nicht gegen Hindernisse anschlägt, oder dass die Arme im maximal möglichen Abstand zwischen ihnen gehalten werden, oder sogar, dass die Gelenke weitestgehend von ihren Enden entfernt sind, etc. etc. von "objektiven Funktionen", deren Optimierung eine einzigartige Lösung der Reverse-Kinotics gibt es Bizzeffe. am interessantesten ist jedoch die Zielfunktion, die die Geschwindigkeiten der Gelenke optimiert. wenn wir tatsächlich anstelle der Rückseite des Jacobianos die linke Pseudo-Inverse verwenden:

Pseudoinversasx (j) = [J(trasposto) * J ]^-1 * j(übersetzt)

Wir lösen auf den minimalen Quadraten das unbestimmte Problem der Umkehrkinematik, so dass dadurch die Trajektorie im Raum der Gelenke, die die gewünschte Geschwindigkeit im Arbeitsraum realisiert, mit der gleichen Zeit die Norm von q' kleiner als das Unendliche möglich ist.

 

[Fulvio Romano]

Dualität der CinetostasisAnalyse der elementaren Arbeit, die durch einen Manipulator und seine Gelenke während einer stufenlosen Verschiebung erreicht wird, ist es möglich, folgende Gleichung zu erreichen:

tau = j(übersetzt) * Bereich

wobei tau der Vektor von Paaren zu den Gelenken ist, und die Trägerkraft im Arbeitsraum. ähnelt der Gleichung:

♪

Oder? nur, dass wir im ersten Mitglied die Welt der Gelenke in der zweiten realen Welt haben. Diese Besonderheit wird gerade als "cinetstatische Duktalität" bezeichnet. was für die Kinos wahr ist, ist das Gegenteil ("Inversion der Welten") für statische.
Wir stellen uns den üblichen Planarmanipulator vor, wir stellen uns auch nur zwei Arme vor. wenn die beiden Arme so groß sind, dass der Arm groß ist, haben beide eine große Geschwindigkeit (x') des Endorgans. Daher bedeutet es, dass bei gleicher Geschwindigkeit zu den Gelenken, wenn in dieser Position die Geschwindigkeit groß ist, es bedeutet, dass es groß ist die Norm von j. aber dann wird auch die Norm von j (übersetzt) groß sein. Aber dann, im gleichen Bereich, wird die Tau großartig sein. In dieser Position wird es daher große Paare an die Gelenke nehmen, um auch kleine Kräfte an das Endorgan zu gewinnen.
Im Wesentlichen haben wir entdeckt, was intuitiv ist, was in Positionen, für die der Manipulator große Geschwindigkeiten zu erzeugen hat, kleine Kräfte erzeugen kann, und umgekehrt.
Ellipsoide der ManipulationDie cynetstatische Dualität ist geometrisch mit einem eleganten und interessanten Instrument, d.h. dem Ellipsoid der Manipulation zu sehen. In der Tat die Ellipsoide, sehen wir, warum. Dieses Werkzeug kann sowohl in der Designphase des Roboters verwendet werden, um seine Geschicklichkeit zu bewerten, als auch in der Planungsphase der Trajektorie zu verstehen, ob es in "poco destre" Bereiche geht.

wir sind im Raum der Geschwindigkeit zu Gelenken. Wir stellen uns vor, eine Kugel mit mittlerem Ursprung und einheitlichem Radius zu zeichnen (natürlich sprechen wir von einer Hypersphäre der Größe gleich der Anzahl der Gelenke des Manipulators). wir können die Gleichung dieser Kugel als Standard der Geschwindigkeit gleich einem schreiben:

* q' = 1

aber wie wir wissen, dass v = j(q) q', dann wird die obige Gleichung:

v(übersetzt) * [J * J(trasposto)]* v = 1

d.h. die geometrische Darstellung eines Quadriks, für die Genauigkeit eines im Geschwindigkeitsraum im Arbeitsraum definierten Ellipsoids (in Größe). durch die mechanische Struktur des Manipulators, kurz gesagt, die Kugel "verformt" , "festigen" in die Richtungen, wo es mehr Neigung hat, Geschwindigkeit zu erzeugen, und "contraendosi" in der gegenüberliegenden. Messen des Radius der Ellipse in einer bestimmten Richtung kann gemessen werden, indem der Manipulator in dieser Richtung Geschwindigkeit erzeugen kann. Je mehr Ellipsoid wie eine Kugel aussieht, desto mehr Manipulator ist in der Lage, Geschwindigkeit in isotroper Weise zu erzeugen.
Darüber hinaus das Volumen des Ellipsoids (der bestimmende Faktor des Kerns der quadratischen Form, oder Det[J*J(trasposto)] ) durch ein Maß für die totale "Dextremität" des Manipulators.
wenn der Manipulator in Singularität verliert an Geschicklichkeit, und tatsächlich wird die Bestimmung des Kerns Null, ist das Ellipsoid degeneriert in einem Punkt.

Angenommen, wir tun dasselbe, aber anstelle der Geschwindigkeiten der Gelenke verwenden wir die Paare. Für Ähnlichkeiten werden die beiden Gleichungen:

tau (übersetzt) * tau = 1
Bereich(transponiert) [J * J(trasposto)] Bereich = 1

wenn wir vorher über Ellipsoid der Manipulation in der Geschwindigkeit sprachen, sprechen wir darüber in Kraft. die gleichen Reden vor, mit dem einzigen Unterschied, dass jetzt der Kern der Quadrik ist die Rückseite der vorherigen. das Ellipsoid der Manipulation in Kraft hat dann die größere Achse an der unteren Achse des Ellipsoids der Manipulation in der Geschwindigkeit, und umgekehrt. Wie wir zuvor gesehen hatten, wo es größere Neigung zur Erzeugung von Geschwindigkeit gibt, wird es weniger Neigung, Stärke zu erzeugen.

der Manipulator kann daher als "mechanischer Transformator" von Geschwindigkeit und Kräften aus dem Raum der Gelenke zum Arbeitsraum betrachtet werden.

in den folgenden Zahlen sehen Sie:

1. Vergleich der Ellipsoide der Manipulation in Geschwindigkeit und Stärke für einen planaren Manipulator zu zwei Armen in unterschiedlichen Positionen.

2. Vergleich von Ellipsoiden für einen dreiarmigen Planarmanipulator. Das ähnelt einem menschlichen Arm und man kann die beiden Fälle unterscheiden. Im ersten Fall stellen wir uns vor, auf einem Blatt Papier zu schreiben. Es ist natürlich, den Ellbogen zu unterstützen und das Handgelenk zu bewegen. Manipulative Ellipsoide zeigen, dass bei dieser Ausgestaltung der Manipulator in vertikaler Richtung die untere (oder fast) Kraftachse ellipsoid und in horizontaler Richtung, die in Geschwindigkeit. In der Tat erfordert die Aufgabe eine feine Kontrolle des vertikalen Druckes des Stiftes auf dem Blatt, und horizontale Geschwindigkeit mit guter Rechtschreibung zu schreiben. schlechte Fähigkeit, Stärke oder Geschwindigkeit in einer Richtung zu erzeugen, bedeutet eine größere Kontrolle.
der zweite Fall ist immer der menschliche Arm, der zum Beispiel eine Bowlingkugel werfen muss. hier ist eine vertikale Richtung Kraft und Geschwindigkeit in der horizontalen erforderlich. der so angeordnete Arm hat genau diese Haltung, wie von den Ellipsen sichtbar.