Únase al foro de diseñadores!
Su experiencia es vital para la comunidad. Únase a nosotros y aporte sus conocimientos.
Únase ahora al ForoComparta, aprenda y crezca con los mejores profesionales del sector.
Resumen
En la primera parte de esta serie de discusiones, exploro y verifico la relación entre los cálculos manuales y la respuesta dependiente del tiempo de un objeto que se deja caer sobre una superficie rígida y qué deflexiones y tensiones se producen durante ese periodo de impacto. Los conceptos que se tratan a continuación son imprescindibles para comprender cómo configurar y resolver un análisis estructural transitorio con ANSYS Mechanical.
Figura 1: Barra durante el impacto (con escala de deflexión exagerada).
La figura 1 ilustra nuestra barra de ejemplo después de ser dejada caer y muestra lo que ocurre durante el periodo de impacto. El resto del documento explora cómo podemos configurar y analizar este tipo de sistema y comparar nuestros progresos con los cálculos manuales habituales.
He aquí una lista de los temas que se tratan en esta discusión (por orden de aparición):
- Energía potencial
- Energía elástica
- Rigidez direccional
- Análisis estructural estático
- Fuerza de compresión media
- Energía cinética
- Velocidad de impacto
- Periodo de impacto
- Frecuencia natural
- Masa efectiva modal
- Análisis estructural transitorio
- Análisis Duración
- Frecuencia
- Desplazamiento transitorio complejo y resultados de tensión
- Tensión de compresión media
Detalles
Empecé a explorar la relación entre los cálculos manuales y los resultados de deflexión máxima y tensión producidos por eventos dinámicos, como el impacto de un objeto contra otro. Utilicé ANSYS Mechanical como medio para verificar los supuestos y proporcionar mayores detalles sobre estos eventos dinámicos. Tengo fe en el método de los elementos finitos y espero poder compartir mis hallazgos con ustedes.
Comencé mi exploración con un ejemplo sencillo de una barra cilíndrica que se deja caer sobre una superficie rígida. En este escenario, y en todos los escenarios asociados a esta discusión, asumo que existe un comportamiento elástico del material y que ninguna de las cargas provocaría plasticidad o daños. Esto significa que existe conservación de la energía dentro de la geometría.
Durante este proceso, hice una serie de suposiciones y realicé análisis de elementos finitos para verificar o rebatir esas suposiciones. Este proceso me hizo formular más preguntas, analizar y obtener más respuestas. Al final, soy capaz de describir con confianza muchos aspectos de este evento dinámico, todos los cuales presentaré de la forma más concisa posible.
Empecemos por la idea más sencilla.
Este primer ejemplo explora la caída de una barra cilíndrica sobre una superficie dura. La barra tiene un diámetro de 25,4 mm y una longitud de 254 mm y una densidad de masa de 7,85e-06 [kg/mm³]. Esta barra se dejará caer desde 1 metro de la cara inferior.
Figura 2: Barra cilíndrica
En esta circunstancia, la energía potencial debe ser igual a la energía elástica.
Energía potencial:

Energía Elástica:

Igualemos la Energía Potencial de nuestro cilindro que cae con su Energía Elástica para saber si podemos predecir las deflexiones con exactitud.
Supongamos que la barra se dejará caer de forma que se desplace en la dirección Y negativa. Por lo tanto, el primer paso será determinar la rigidez de nuestra geometría en la dirección Y.
Para nuestro modelo, esta rigidez puede deducirse teóricamente, así como utilizando el método de elementos finitos de aplicar una carga conocida y dividir esta carga por la desviación calculada en la dirección Y. Esto nos permitirá comparar los resultados de nuestra estimación de elementos finitos con el valor derivado teóricamente y desarrollar confianza en nuestra metodología.
Derivemos nuestra rigidez teórica. Para la dirección Y, se aplicará la siguiente fórmula:

Ahora, calculemos también la rigidez de la geometría mediante un análisis de elementos finitos por dos métodos diferentes, para que comprendamos las distintas consideraciones que conllevan los diferentes tipos de cargas.
Aquí consideramos una base fija mientras aplicamos una fuerza al extremo distal de nuestro cilindro tal que la fuerza de reacción en la base es igual en magnitud y opuesta en signo a la fuerza aplicada en la parte superior del cilindro. La magnitud de esta carga de compresión no es crítica, siempre que las propiedades de nuestro material sean lineales y que no estemos considerando la no linealidad de la geometría (gran deformación).
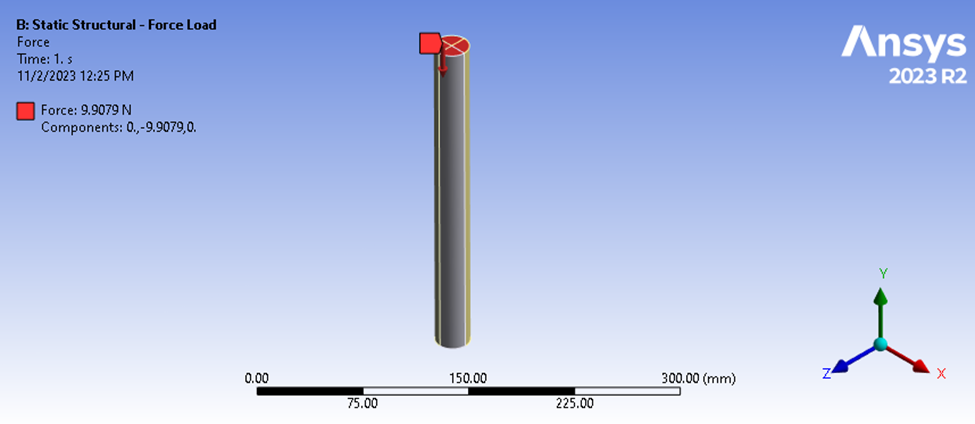
Figura 3: Análisis estructural estático del vástago cargado por su parte superior y apoyado en su parte inferior.
En este escenario, se aplica una carga de 9,9079 N a la superficie superior mientras que la superficie inferior se fija a partir de los desplazamientos Y. La magnitud de esta carga se aclarará más adelante.
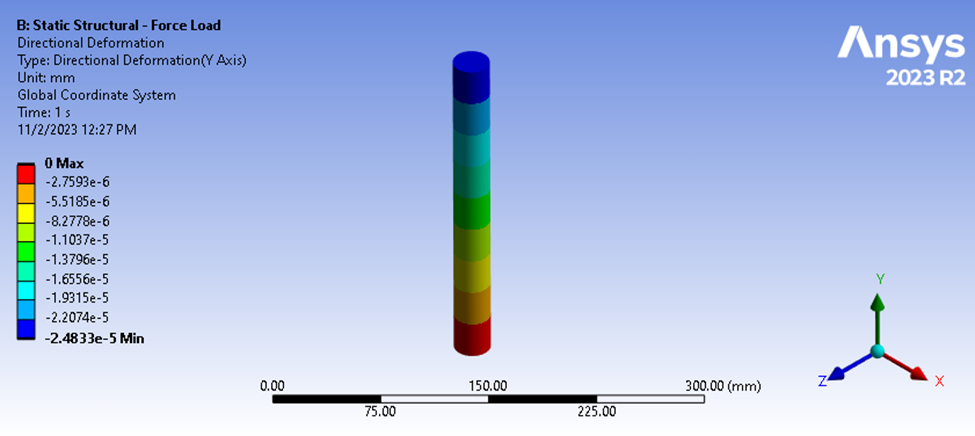
Figura 4: Resultados de la deflexión estructural estática
La resolución del análisis estructural estático muestra una magnitud máxima para nuestra deflexión de compresión de 2,4833e-5 mm. Basándonos en nuestra carga de 9,9079 N, podemos calcular la siguiente rigidez media.
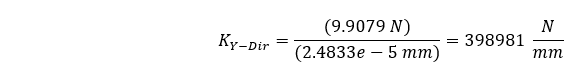
Se puede ver que el enfoque de elementos finitos demuestra sólo un 0,00125% de diferencia con el enfoque teórico. Esto nos hace sentir bien 😊
A continuación, consideremos un tipo diferente de carga, como la carga de gravedad. Aquí, la fuerza se elimina de la superficie superior, pero la superficie inferior permanece constreñida, y la gravedad se aplica a 9806,6 mm/seg^2. La fuerza de reacción en la base es de 9,9079 N, pero la fuerza que actúa sobre la superficie superior es definitivamente cero. Los resultados de la deflexión muestran una magnitud de deflexión diferente de 1,2421e-5 mm.
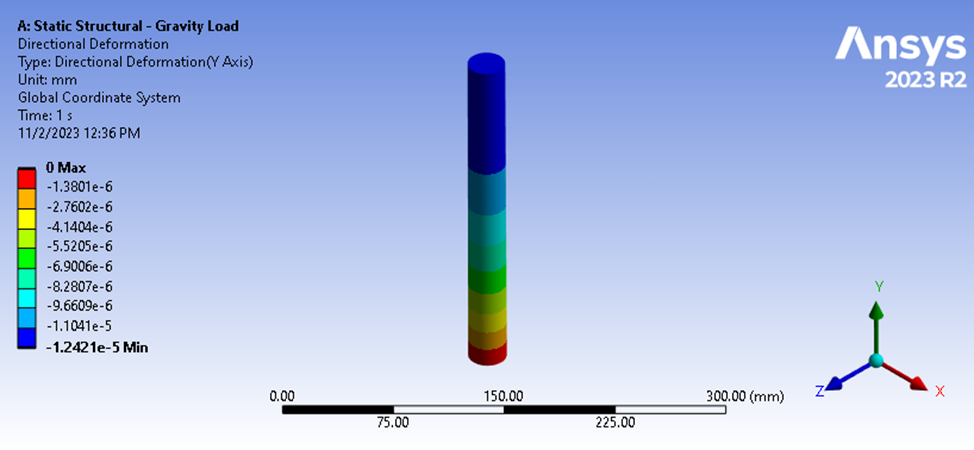
Figura 5: Resultados de la deflexión del análisis estructural estático
Si intentáramos calcular la rigidez mediante la misma forma de la ecuación anterior, llegaríamos a un valor incorrecto porque no estaríamos considerando la fuerza de compresión media que actúa a través de nuestra geometría. En este caso, nuestra fuerza de compresión media puede estimarse fácilmente ya que nuestra geometría tiene una sección transversal constante y nuestra rigidez media estimada puede calcularse como sigue.
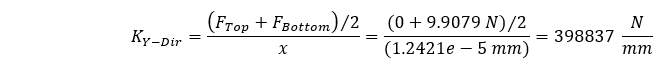
Esta estimación demuestra una diferencia del 0,0348% con respecto a nuestro valor calculado teóricamente. Por lo tanto, mediante dos métodos de carga diferentes, podemos estimar con seguridad la rigidez en la dirección de la geometría.
Sustituyendo nuestra rigidez direccional estimada, junto con nuestro modelo y las propiedades del material, podemos estimar nuestra deflexión máxima a continuación.
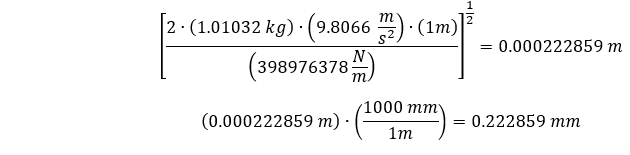
Que es de unos ~0,223 mm. Ahora necesitamos un modelo estructural transitorio para simular las deflexiones en y después del momento del impacto de nuestra barra cilíndrica con el suelo.

Figura 6: Modelo de análisis estructural transitorio y restricciones
Nuestro modelo supone que la barra se mueve a 4428 mm/seg en la dirección Y negativa. Esta es la velocidad que alcanzaría la barra si se dejara caer 1 m. Podemos calcularla igualando la Energía Potencial de la barra con su Energía Cinética en el instante del impacto.
Energía cinética:
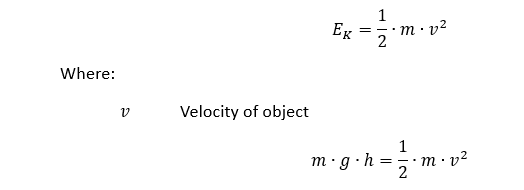
Por lo tanto:

Se añaden restricciones para mantener la estatura vertical de la geometría, mientras que en la base se añade un soporte sólo de compresión. Se define la duración del análisis (más sobre esto más adelante), junto con una tasa de captura frecuente para recoger los resultados.
Los resultados del análisis son complicados, porque a medida que la parte superior de la barra se desvía hacia abajo tras el impacto, la parte inferior de la barra puede comprimirse ligeramente debido a la rigidez asociada al apoyo sólo a compresión. Es la diferencia de deflexión entre estas dos superficies la que describe la compresión global de la barra.
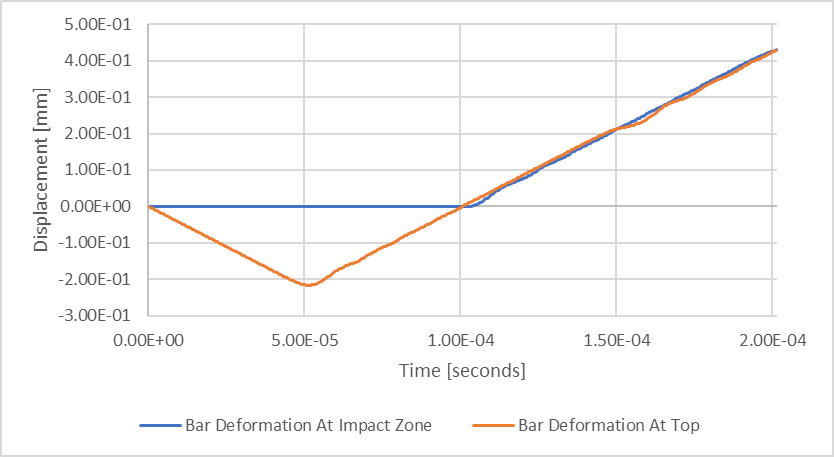
Figura 7: Resultados de la deflexión estructural transitoria
El periodo plano de la línea azul, «Deformación de la barra en la zona de impacto», demuestra ese periodo para el que se produce el contacto en la base, o la permanencia asociada al impacto. Si volvemos a trazar nuestros datos para centrarnos en este periodo, podremos hacer más fácilmente varias observaciones.
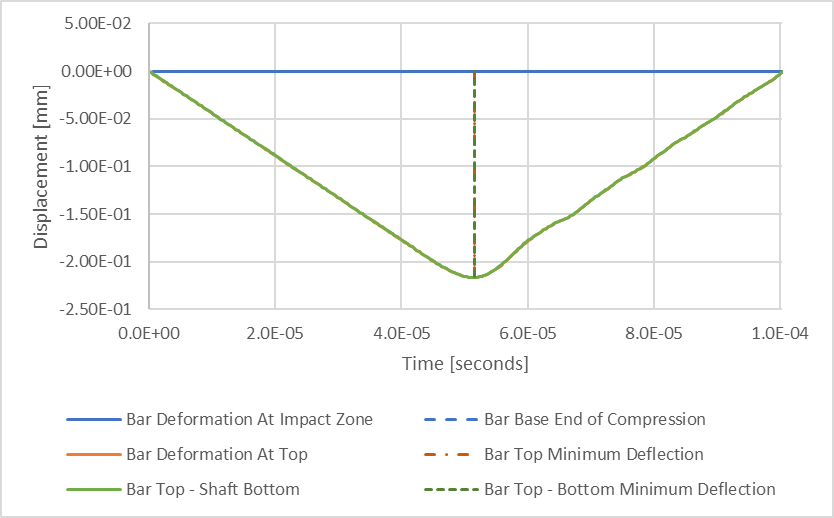
Figura 8: Resultados de la deformación por compresión estructural transitoria
He añadido una línea verde que representa la diferencia entre las deflexiones de la superficie superior e inferior de la barra, lo que resulta en la compresión total de la barra en función del tiempo. Las dos líneas discontinuas verticales representan los intervalos de tiempo asociados a los resultados mínimos de las líneas naranja y verde. Se puede observar que la compresión mínima de la barra se produce al mismo tiempo que la compresión mínima de la parte superior de la barra. A partir de esto, podemos estimar que la compresión máxima de nuestra barra es de 0,216 mm, que es algo menos de un 3% menor que nuestra deflexión máxima estimada de 0,223 mm.
Sin embargo, hay más cosas que explorar y aprender de este ejemplo y sus resultados.
Visitemos ahora el aspecto de la configuración de un análisis estructural transitorio, y abordemos específicamente el periodo de tiempo asociado a nuestro evento y determinemos cómo podemos estimar este periodo para cualquier geometría.
Si nos fijamos en el momento en que la línea azul cruzó del desplazamiento negativo al positivo (0,00010026 segundos), que equivale al periodo asociado a la compresión de nuestro eje.
Nuestro eje puede considerarse un muelle que rebota. La duración del impacto refleja ½ período de su frecuencia natural en la dirección de la compresión. Por lo tanto, lo siguiente debería ser cierto.

Ahora vamos a explorar si podemos apoyar esta teoría, así como la forma de estimar la frecuencia natural para esta, y cualquier geometría que esperemos analizar en el futuro.
Podemos cambiar el soporte «sólo compresión» aplicado al modelo de prueba anterior, con una restricción de dirección Y en esas mismas superficies y resolver directamente para nuestra frecuencia de vibración longitudinal en ANSYS.
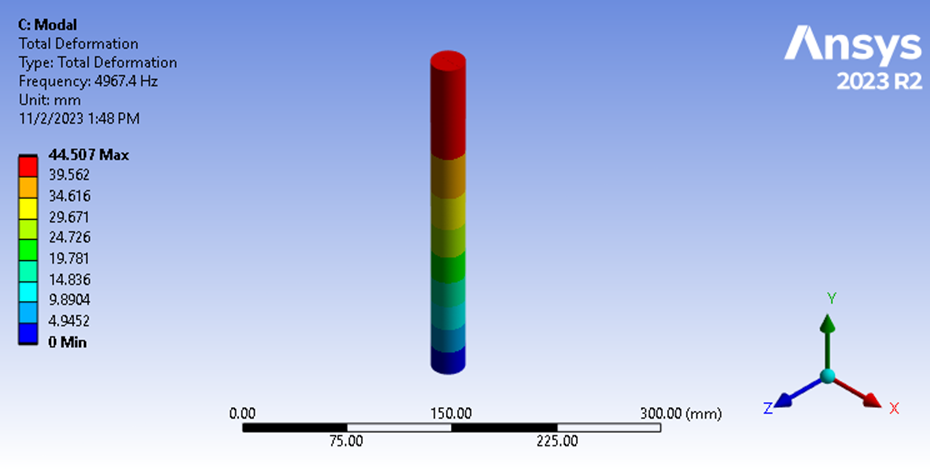
Figura 9: Frecuencia fundamental del análisis modal
Aquí vemos que la frecuencia de vibración longitudinal es de 4967,4 Hz. Esto demuestra que nuestra estimación de la frecuencia natural basada en nuestros resultados de desplazamiento estructural transitorio fue precisa dentro de un 0,4%. Este hallazgo confirma nuestra teoría de que la duración del impacto es igual a ½ del periodo de la frecuencia fundamental para el ablandamiento de dos objetos que impactan.
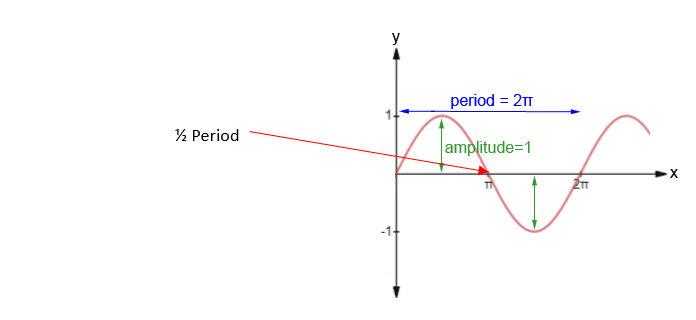
Figura 10: Periodo de impacto
En nuestro ejemplo de análisis, sólo tenemos una parte y suponemos que el soporte vertical sólo a compresión representa otro objeto muy rígido. Por lo tanto, nuestro eje es el más flexible de estos dos socios de impacto. Nuestro análisis estructural transitorio se definió para tener una duración de análisis igual al periodo de esta frecuencia natural, y esperamos que el impacto se produzca durante la primera ½ parte de este periodo.
Pero, ¿cómo calculamos esta frecuencia natural si estamos configurando un análisis estructural transitorio?
Podemos hacer lo que acabo de demostrar, que es realizar un análisis modal de la geometría, mientras utilizamos restricciones para mantener la postura de impacto y resolvemos directamente para la forma modal de compresión de impacto. Pero, ¿hay alguna forma analítica de lograr lo mismo?
Para explorarlo, necesitamos calcular la frecuencia natural de nuestra geometría en la dirección del impacto, que puede calcularse como sigue.

Ya hemos explorado cómo podemos estimar la rigidez direccional, pero ahora consideremos un par de ejemplos para comprender mejor la consideración de la masa efectiva modal.
La masa total de nuestro sistema es
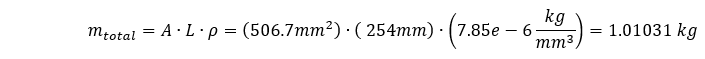
La masa efectiva de nuestro sistema será menor que la masa total, ya que un extremo de nuestra geometría está constreñido. Puede resultar difícil estimar la cantidad de masa que participará en función de la complejidad de nuestra geometría y de las restricciones utilizadas para fijar la geometría. En nuestro caso, la geometría es simple y para las secciones transversales extruidas que están fijadas en un extremo, a menudo se deduce que la masa efectiva es igual a 1/3 de la masa total del sistema. Si este fuera el caso, nuestra frecuencia fundamental sería la siguiente:
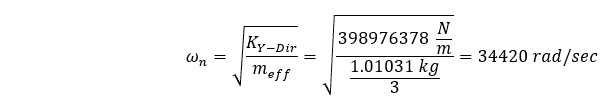
Que puede enunciarse de forma más reconocible como:
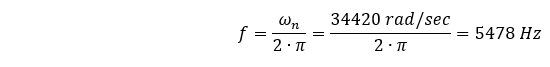
Este valor (5478 Hz) es más de un 10% mayor que nuestra frecuencia natural (4967,4 Hz) calculada por el método de los elementos finitos… ¿por qué?
La respuesta está relacionada con la estimación de la masa efectiva modal. Si nos sentimos seguros del cálculo de la rigidez longitudinal (…lo hacemos…), entonces podemos cambiar la configuración de nuestro modelo para verificar más fácilmente el cálculo de nuestra frecuencia fundamental.
Estableceremos la densidad de masa de nuestro material para nuestro modelo igual a cero, luego añadiremos 1,01031 kg de masa al extremo distal de nuestra geometría, lo que debería producir la siguiente frecuencia natural.
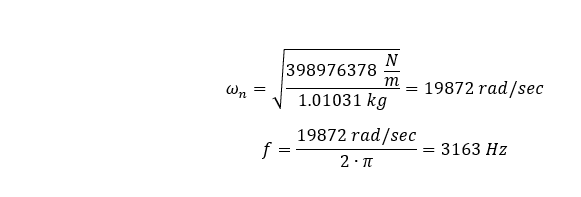
Tras ejecutar el análisis de elementos finitos, vemos que la frecuencia longitudinal fundamental es de 3154,6 Hz.
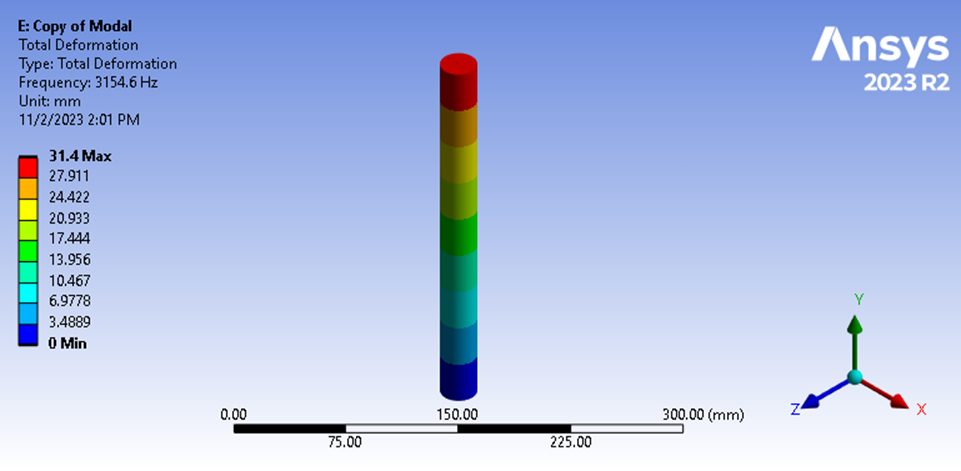
Figura 11: Frecuencia fundamental del análisis modal
Esto refleja una diferencia del 0,27% con respecto a nuestro cálculo manual. Por lo tanto, desarrollamos más confianza en el método de elementos finitos, e identificamos una debilidad en nuestra estimación de la masa efectiva utilizada en nuestro cálculo manual utilizando masa distribuida a lo largo de nuestra geometría.
Reordenando nuestra ecuación, podemos resolver esta masa efectiva teniendo en cuenta la frecuencia natural calculada por ANSYS considerando la masa distribuida de la siguiente manera:
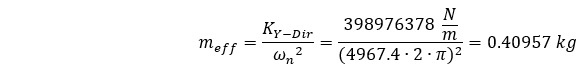
Encontramos que esta masa efectiva es el 0,405 de la masa total del sistema.
Por lo tanto, para otras geometrías, y más complejas, podemos esperar que esta fracción de masa sea única y difícil de derivar teóricamente y que podamos resolver con fiabilidad la frecuencia natural utilizando el método de los elementos finitos.
Ahora que entendemos cómo determinaremos la frecuencia natural para una geometría dada, necesitamos determinar a qué frecuencia debemos recoger los resultados del análisis durante nuestro análisis transitorio.
Para ello, debemos considerar cómo afecta el tamaño del paso de análisis desde dos perspectivas diferentes. Una perspectiva es en términos de lo que uno podría esperar utilizando una caracterización lineal a trozos de una respuesta no lineal, como una onda sinusoidal. La otra perspectiva se refiere a cómo cambian los resultados reales del análisis en función del cambio en la frecuencia de la tasa de captura. Como estamos considerando un problema de impacto y hemos supuesto que el periodo de impacto está asociado a la vibración fundamental de nuestro componente flexible, tiene sentido explorar la relación entre el tamaño del paso y cómo afecta a la precisión que representa una curva sinusoidal.
Para evaluar esta relación, compararemos la media ponderada de la magnitud para la primera mitad de la curva sinusoidal con la media teórica de este mismo tramo, que es igual:
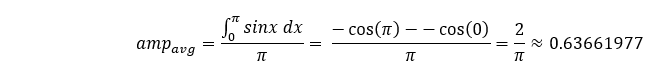
Ahora exploramos con qué precisión, utilizando un número diferente de pasos, representamos esta curva sinusoidal, luego utilizamos la regla trapezoidal para calcular el área bajo la curva para la primera mitad, luego dividimos esa área por el periodo de ese tramo.
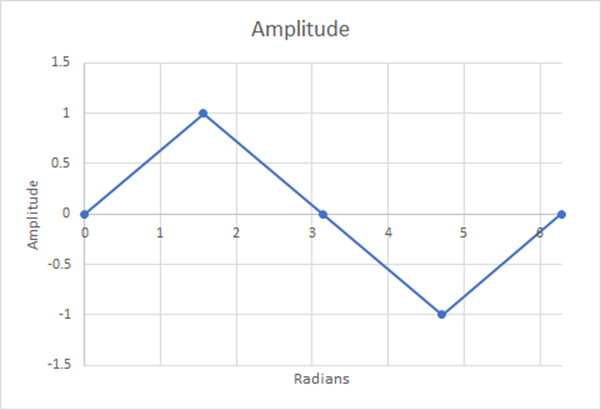
Figura 12: 4 pasos; media ponderada estimada=0,5; 21,46% de diferencia
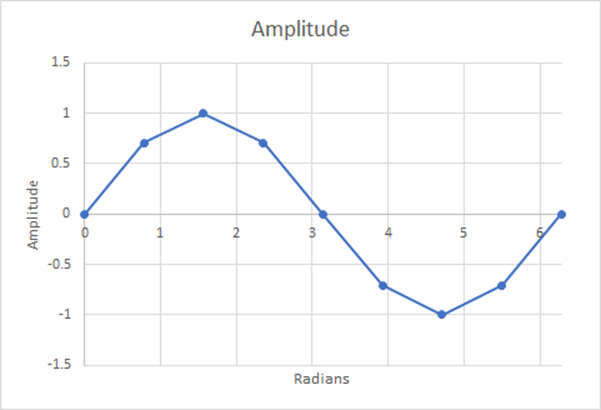
Figura 13: 8 pasos; media ponderada estimada=0,60536; 5,19% de diferencia
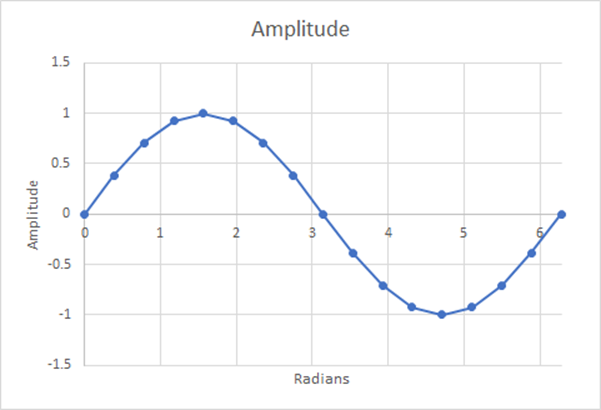
Figura 14: 16 pasos; media ponderada estimada=0,6284; 1,29% de diferencia
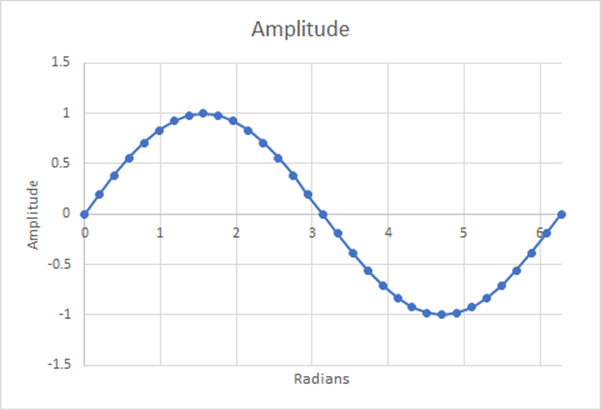
Figura 15: 32 pasos; media ponderada estimada=0,6346; 0,32% de diferencia
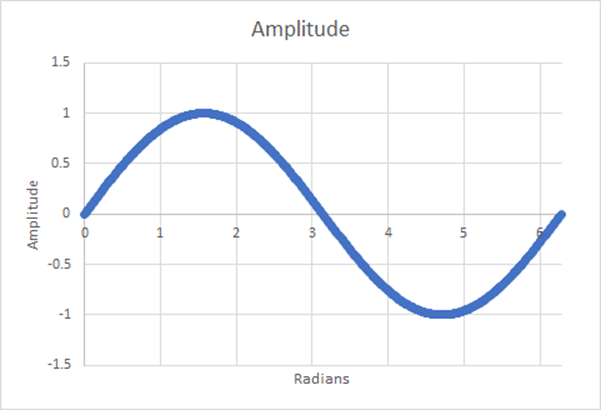
Figura 16: 512 pasos; media ponderada estimada=0,6366; 0,001% de diferencia
De hecho, nunca conseguimos una concordancia perfecta con el valor teórico, y podemos representar gráficamente cómo cambia esta precisión a medida que aumenta el número de pasos temporales, como se ilustra a continuación.
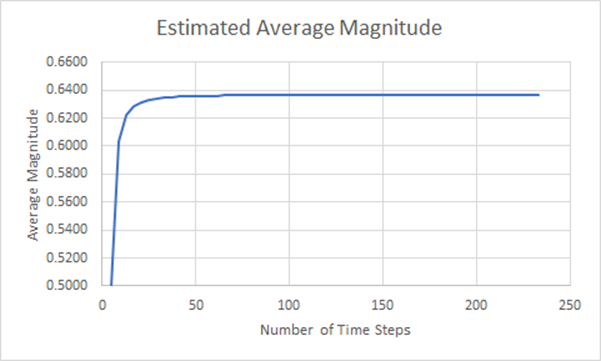
Figura 17: Gráfico de convergencia de la magnitud media estimada
A partir de este examen, podemos ver que los grandes aumentos de precisión se producen rápidamente a medida que aumentamos el número de pasos en nuestra aproximación. Pero esto no tiene en cuenta cómo evolucionan los resultados a medida que aumenta el número de pasos temporales.
Para explorar la influencia en los resultados del análisis, trazaremos nuestros resultados de compresión de la varilla máxima, en función del tiempo, considerando diferentes números de pasos temporales definidos en la solución.
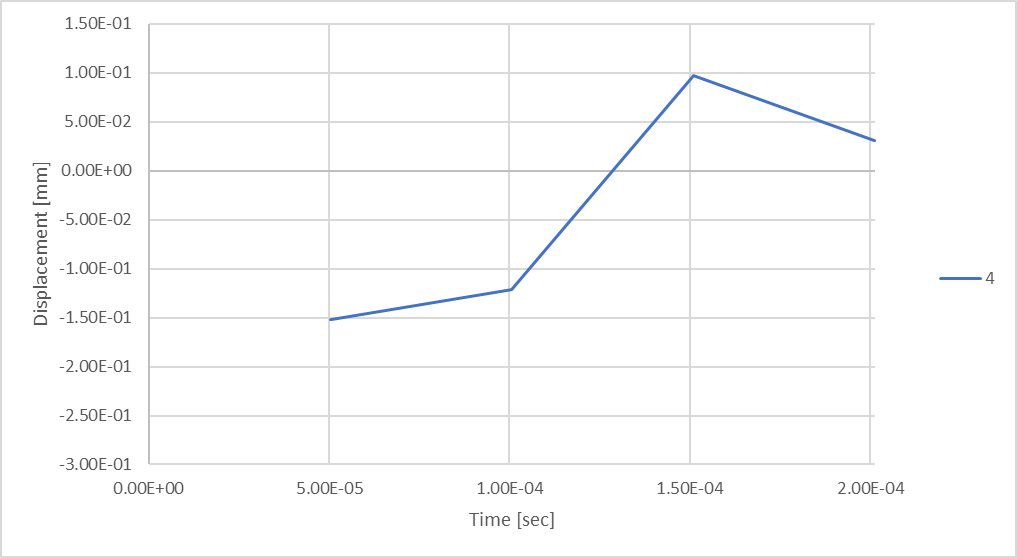
Figura 18: Desplazamiento de la varilla mientras se consideran 4 pasos de tiempo.
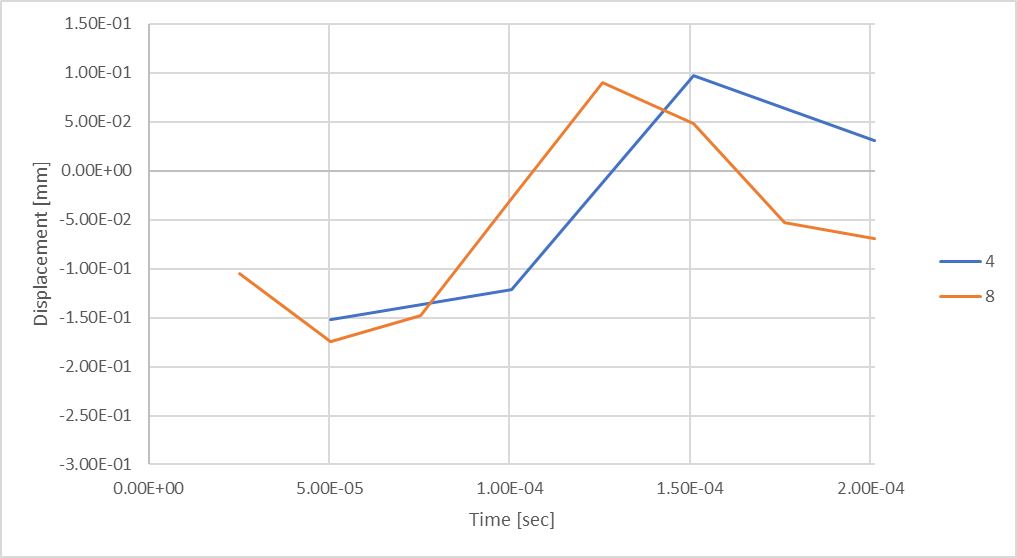
Figura 19: Desplazamiento de la barra considerando 8 pasos temporales.
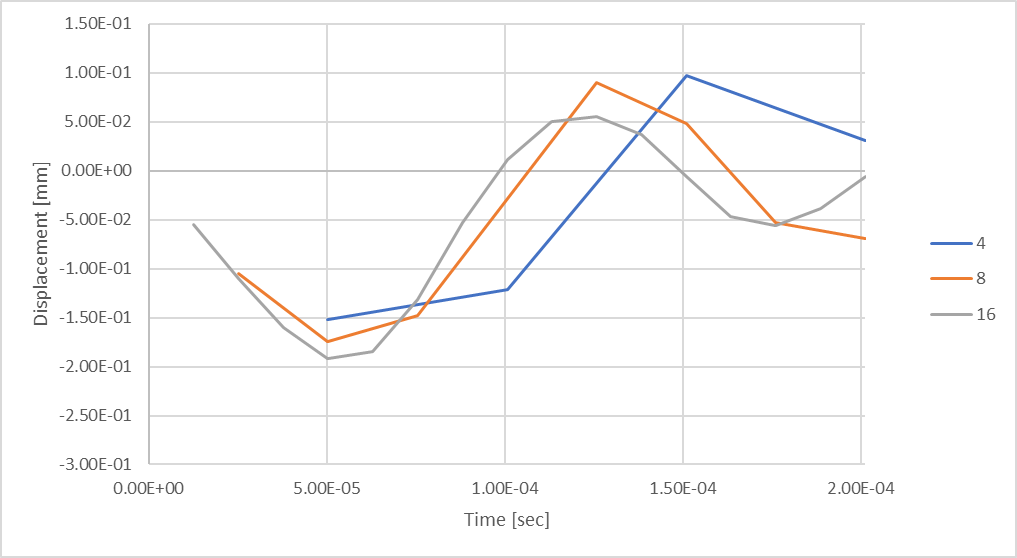
Figura 20: Con 16 pasos de tiempo, observamos mayores desplazamientos de compresión de la varilla.
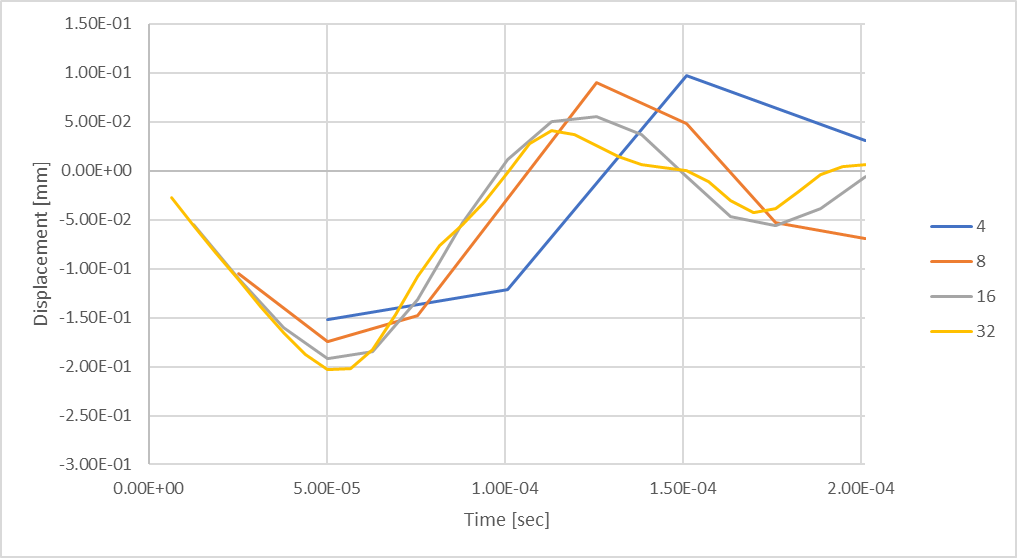
Figura 21: Deflexión máxima transitoria de la varilla utilizando 32 pasos de tiempo.
Basándonos en nuestro análisis previo de cálculo de la magnitud media sinusoidal, descubrimos que considerando 32 pasos, deberíamos esperar hasta un 0,32% de diferencia con los resultados teóricos. Sin embargo, podemos ver que la respuesta del desplazamiento de compresión de nuestra barra sigue formándose en comparación con las exploraciones previas de pasos de tiempo. ¿Qué ocurre si consideramos pasos de tiempo adicionales?
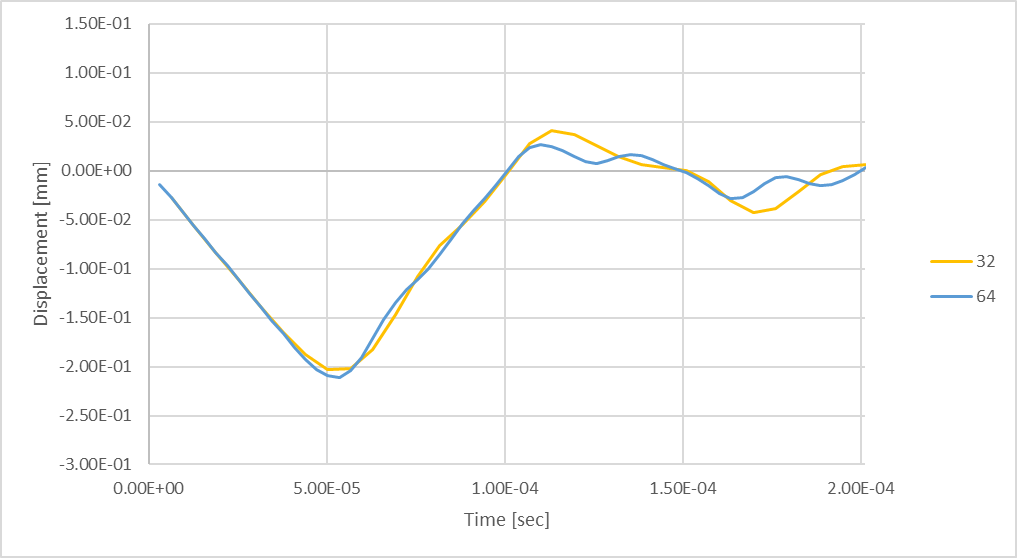
Figura 22: Deflexión máxima transitoria de la varilla utilizando 64 pasos de tiempo.
64 pasos de tiempo produce una deflexión máxima de la varilla a compresión ligeramente mayor, pero en su mayor parte similar, sin embargo, hay indicios de que se desarrollan oscilaciones de mayor frecuencia durante el rebote de la varilla.
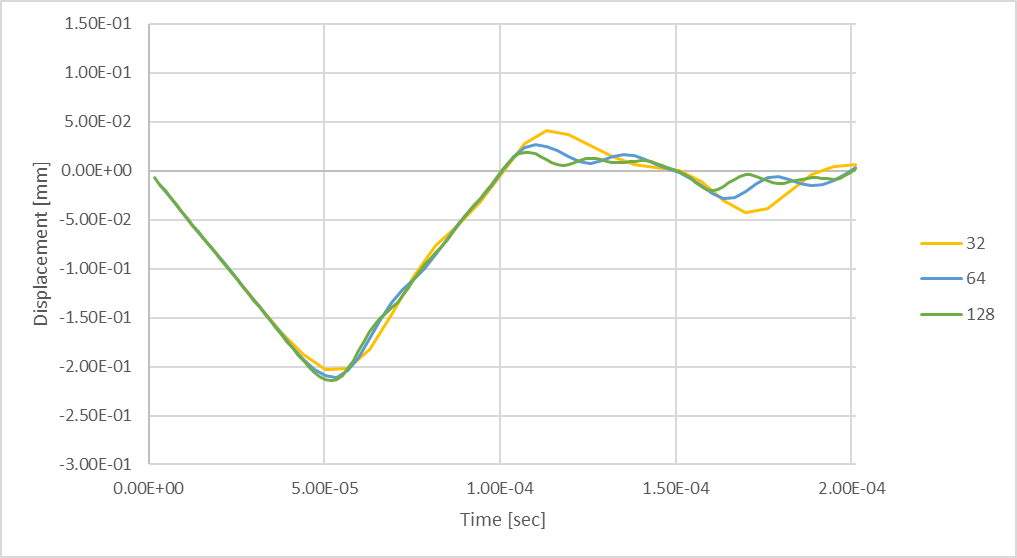
Figura 23: Deflexión máxima transitoria de la varilla utilizando 128 pasos de tiempo.
Considerando 128 pasos de tiempo la compresión máxima en el vástago es mayor que con el menor número de pasos de tiempo. La deflexión máxima por compresión es un 6% mayor que la producida al considerar 32 pasos de tiempo.
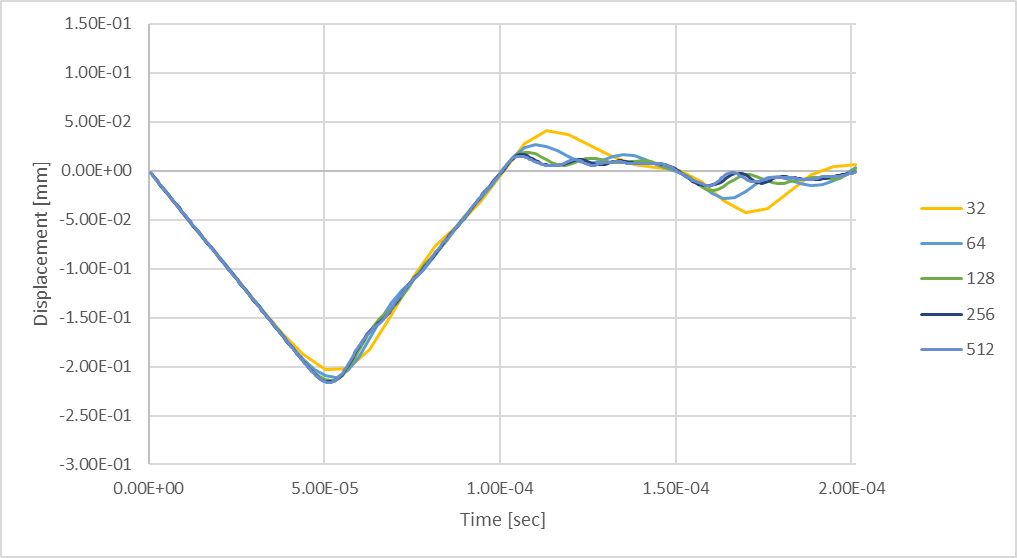
Figura 24: Deflexión máxima transitoria de la varilla utilizando hasta 512 pasos de tiempo.
La comparación de los resultados del análisis de 256 pasos temporales con los producidos al considerar 512 pasos temporales muestra que al considerar más pasos temporales se puede calcular una mayor resolución de la respuesta dinámica. El siguiente gráfico ilustra cómo pueden cambiar nuestras deflexiones máximas de la barra de compresión en función del número de pasos temporales considerados en un análisis estructural transitorio.
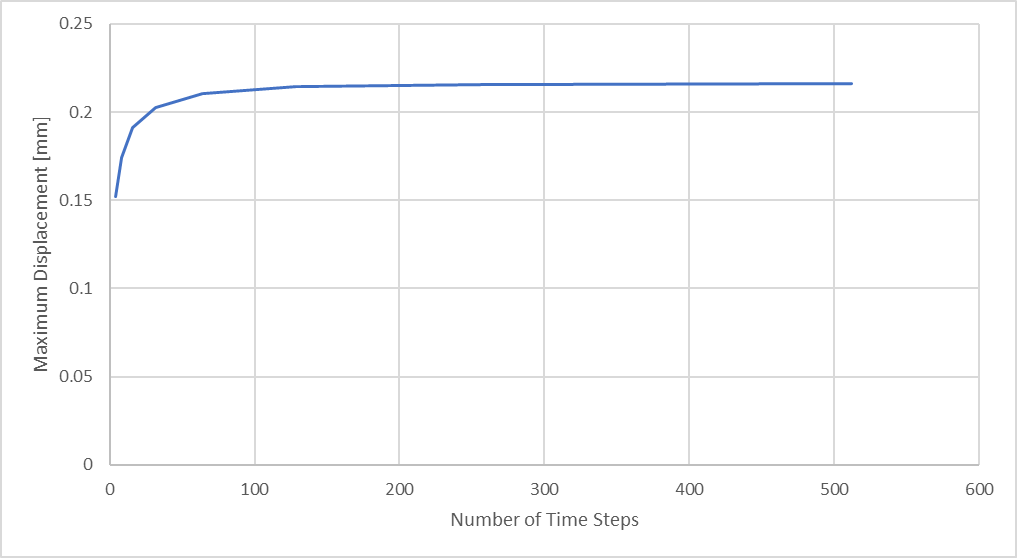
Figura 25: Desplazamiento máximo a compresión de la varilla frente al número de pasos de tiempo del análisis
Finalmente, para un tamaño de malla dado, llegamos a un punto de rendimientos decrecientes… en el que el esfuerzo que supone un mayor tiempo de análisis y archivos de resultados más grandes no se justifica por un cambio significativo en la magnitud de los resultados.
Basándonos en estas dos consideraciones, podemos ver que utilizando 32 pasos de tiempo, podemos esperar caracterizar una curva sinusoidal con una diferencia de hasta el 0,32%, pero sólo puede producir resultados de desplazamiento con una precisión del 94% en comparación con el mismo análisis que utilizó 512 pasos de tiempo, y sólo dentro del 91% de precisión mientras se compara con nuestra deflexión máxima teórica. En la figura siguiente vemos cómo se comparan nuestros resultados de compresión máxima de la barra con nuestro máximo estimado teóricamente.
| Número de subpasos | Compresión máxima | Max teórico | % Diferencia |
| 4 | 0.152139 | 0.222859 | 31.73% |
| 8 | 0.174023 | 0.222859 | 21.91% |
| 16 | 0.191486 | 0.222859 | 14.08% |
| 32 | 0.202746 | 0.222859 | 9.03% |
| 64 | 0.210712 | 0.222859 | 5.45% |
| 128 | 0.214455 | 0.222859 | 3.77% |
| 256 | 0.215752 | 0.222859 | 3.19% |
| 512 | 0.216232 | 0.222859 | 2.97% |
Figura 26: Desplazamiento máximo de compresión de la barra frente a los pasos de tiempo del análisis
A medida que se incrementa el número de pasos de tiempo, aumenta la concordancia entre los resultados de nuestro análisis de elementos finitos y nuestro valor derivado teóricamente.
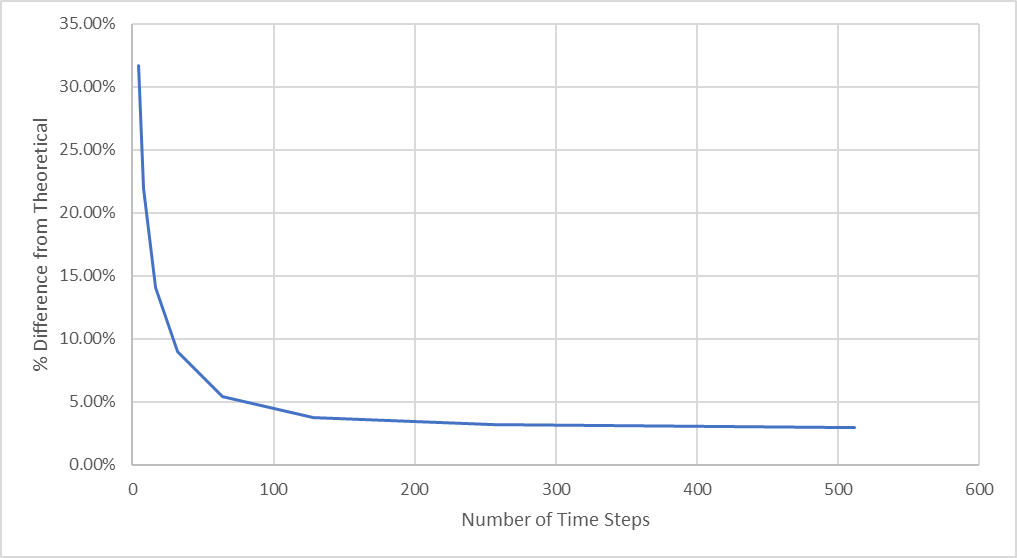
Figura 27: Diferencia porcentual respecto a la deflexión máxima teórica
Vemos en esta figura cómo hay una mejora espectacular hacia la convergencia a medida que el número de pasos temporales se sitúa entre 64 y 128, pero cambia muy poco a medida que se aumenta el número de pasos temporales.
Pero, ¿qué significa todo esto con respecto a otros resultados, como la tensión?
A continuación, trazaré la tensión máxima de von Mises por tiempo para varios escenarios de análisis.
Figura 28: Tensión de von Mises durante la resolución de 32 pasos temporales
Figura 29: Tensión de von Mises durante la resolución de 64 pasos temporales
Figura 30: Tensión de von Mises durante la resolución de 128 pasos temporales
Figura 31: Tensión von Mises durante la resolución de 256 pasos temporales
Figura 32: Tensión de von Mises durante la resolución de 512 pasos temporales
En resumen, esto es lo que vemos al visualizar las tensiones:
| Número de subpasos | Tensión media máxima | Tensión máxima máxima | Diferencia en % de la tensión media |
| 4 | 120.04 | 301.98 | 29.62% |
| 8 | 136.4 | 316.61 | 20.03% |
| 16 | 150.57 | 312.42 | 11.72% |
| 32 | 159.15 | 301.68 | 6.69% |
| 64 | 165.4 | 283.51 | 3.03% |
| 128 | 168.84 | 303.99 | 1.01% |
| 256 | 170.05 | 354.35 | 0.30% |
| 512 | 170.56 | 442.08 | 0.00% |
Figura 33: Desplazamiento máximo de compresión de la varilla frente a los pasos de tiempo del análisis
Podemos ver que las tensiones máximas de impacto se hacen más grandes a medida que aumenta el número de pasos de tiempo, mostrando los valores más grandes al inicio del impacto y haciéndose más pequeños a lo largo del suceso. Las tensiones medias en la varilla sí pasan de cero a un pico en la compresión máxima, y luego vuelven a caer hacia cero una vez finalizado el impacto. Podemos trazar estas tensiones medias máximas a continuación.
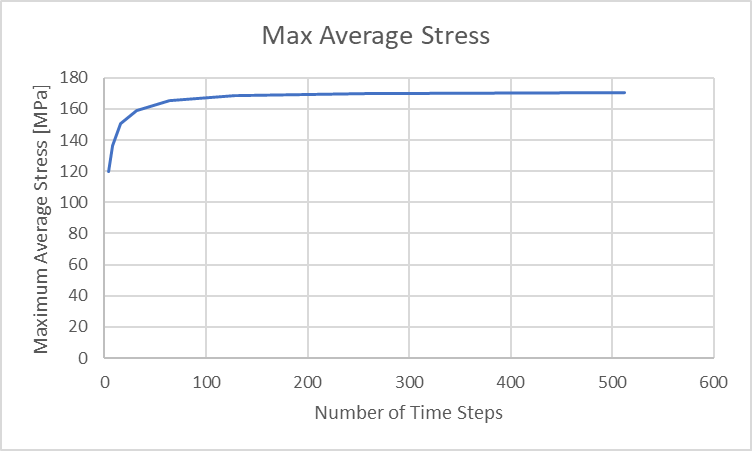
Figura 34: Desplazamiento máximo de compresión de la barra frente a los pasos de tiempo del análisis
Para poner en perspectiva estas tensiones medias máximas, podemos calcular una tensión media máxima teórica en nuestra varilla de la siguiente manera:
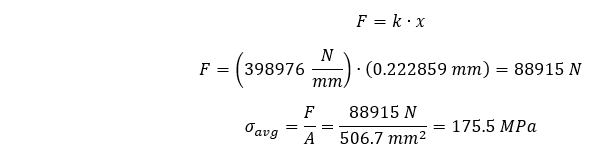
Si volvemos a trazar nuestras tensiones medias máximas frente a la media máxima calculada teóricamente, podemos resumir el % de diferencia de la siguiente manera:
| Número de subpasos | Tensión media máxima | Tensión media máxima teórica | % Diferencia |
| 4 | 120.04 | 175.5 | 31.60% |
| 8 | 136.4 | 175.5 | 22.28% |
| 16 | 150.57 | 175.5 | 14.21% |
| 32 | 159.15 | 175.5 | 9.32% |
| 64 | 165.4 | 175.5 | 5.75% |
| 128 | 168.84 | 175.5 | 3.79% |
| 256 | 170.05 | 175.5 | 3.11% |
| 512 | 170.56 | 175.5 | 2.81% |
Figura 35: Desplazamiento máximo de compresión de la barra frente a los pasos de tiempo del análisis
Una vez más, al igual que en el caso de las flexiones, reconocemos una mejora significativa en la diferencia porcentual de nuestra tensión media máxima en comparación con nuestra tensión media máxima calculada teóricamente al considerar entre 64 y 128 pasos de tiempo para el suceso. Sin embargo, la utilización de más pasos temporales muestra poca mejora en la precisión de nuestros resultados.
Conclusión
Comprobamos que los métodos energéticos utilizados para estimar las deflexiones máximas y las tensiones medias para el evento dinámico, como la caída de un objeto elástico sobre una superficie dura, pueden producir resultados razonables y que las mejoras más significativas en la precisión se producen al considerar entre 64 y 128 pasos temporales para un evento igual en periodo a la frecuencia natural de nuestro objeto impactante, calculada para la dirección del impacto. También descubrimos que el mejor método para aproximar esta frecuencia natural no es mediante cálculos manuales, sino mediante un análisis modal realizado con el método de los elementos finitos, concretamente porque la cantidad de masa efectiva modal participante puede no ser fácilmente e
Únase al foro de diseñadores!
Su experiencia es vital para la comunidad. Únase a nosotros y aporte sus conocimientos.
Únase ahora al ForoComparta, aprenda y crezca con los mejores profesionales del sector.

