Únase al foro de diseñadores!
Su experiencia es vital para la comunidad. Únase a nosotros y aporte sus conocimientos.
Únase ahora al ForoComparta, aprenda y crezca con los mejores profesionales del sector.
La paradoja de los dos condensadores es un provocativo experimento mental creado para exponer algunas de las limitaciones del modelado de circuitos eléctricos, y se han ideado muchas formas diferentes de resolver la paradoja. Yo añadiré una solución que puede modelarse en el programa COMSOL Multiphysics® software y luego ampliarlo para plantear, y responder, una pregunta aún más provocativa: ¿Existen la capacitancia y la inductancia? ¡Sumerjámonos en ella!
La paradoja de los dos condensadores
Este experimento mental se suele presentar como: Considere un dispositivo compuesto por dos condensadores equivalentes, con capacitancia C, conectados en paralelo con un interruptor abierto entre ellos. Todos los cables y condensadores están hechos de materiales ideales, perfectamente libres de resistencia y sin pérdidas. Uno de los condensadores se carga a un potencial, V_i, por lo que la carga almacenada es Q = CV_i. No hay diferencia de potencial en el otro condensador, por lo que no tiene carga almacenada. ¿Qué ocurre cuando se cierra el interruptor?

Esquema de la paradoja de los dos condensadores. Un condensador tiene una diferencia de potencial entre las placas. ¿Qué ocurre cuando el interruptor está cerrado?
En algunas presentaciones de este experimento mental se introduce una pista falsa y se afirma que la carga del primer condensador fluirá hacia el segundo, reduciendo la diferencia de potencial en el primero y aumentándola en el segundo hasta que se alcance un estado estacionario, momento en el que la diferencia de potencial es la misma en ambos condensadores y la mitad de V_i, ya que la misma carga, Q, se reparte ahora entre dos condensadores equivalentes. Sin embargo, esto conduce inmediatamente a una paradoja, porque la energía en cada condensador es W_C = \frac{1}{2} C \Delta V^2. Si la energía inicial es \frac{1}{2} C V_i^2 y la energía final es 2 \frac{1}{2} C\left( V_i/2 \right)^2 = \frac{1}{4} C V_i^2¿dónde fue a parar la otra mitad de la energía?
Hay muchas soluciones disponibles que invocan desde la mecánica cuántica hasta la termodinámica. Es probable que todas estas soluciones sean válidas desde un punto de vista educativo. Sin embargo, muchas de ellas hacen un llamamiento implícito a la realidad diciendo que los cables y los condensadores simplemente deben tener cierta resistencia o deben tener cierta inductancia. Pero, ¿por qué? Al menos en el contexto de un experimento mental, puede ser razonable suponer materiales perfectamente exentos de pérdidas, despreciando así la resistencia. Pero, ¿qué ocurre con la inductancia? En el contexto de este experimento mental, ¿podemos despreciar la inductancia? Sigamos esta pregunta y veamos si proporciona una respuesta interesante…
Una solución sencilla a la paradoja
Nuestro dispositivo está compuesto por dos condensadores ideales sin pérdidas. Pero incluso un condensador ideal debe separar espacialmente sus cargas. Es decir, un condensador debe tener algún tamaño. Y si cada condensador tiene tamaño, entonces debe estar separado por alguna distancia distinta de cero del otro condensador. Así que si redibujamos un poco nuestro diagrama, veremos que tenemos dos condensadores y dos semienrollamientos de diámetro finito de alambre sin pérdidas, a lo largo de los cuales puede fluir una corriente variable en el tiempo. Pero, ¿cómo llamamos a una estructura de este tipo? ¡Un inductor!
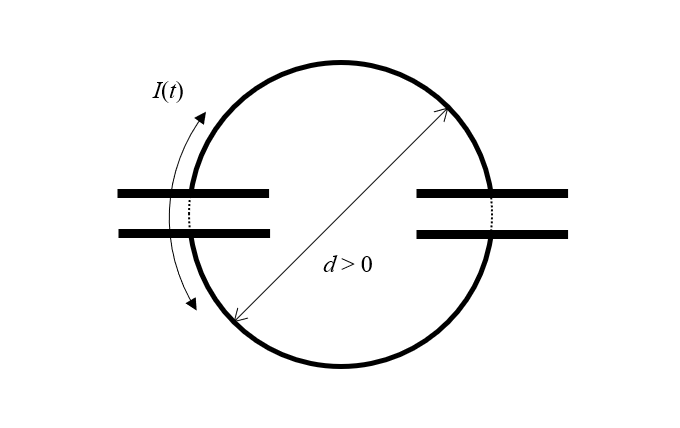
La paradoja puede resolverse dándose cuenta de que la estructura debe tener un tamaño distinto de cero, con corriente fluyendo alrededor de un bucle de área finita, y por tanto es también un inductor.
La estructura que hemos dibujado aquí debe tener un tamaño finito, y por tanto también debe tener inductancia, siempre que exista dentro de nuestro universo, donde el espacio libre tiene permeabilidad magnética. Así que simplemente como consecuencia de que haya un condensador en nuestro circuito, también debe haber un inductor en el circuito. De hecho, la cosa se pone aún mejor: Si tenemos un inductor, incluso uno sin pérdidas, cualquier corriente variable en el tiempo que fluya a través de él provocará un campo eléctrico que existe entre las espiras del inductor, ¡y por tanto cualquier inductor que añadamos a este circuito también actúa como un condensador! Podríamos seguir este hilo de la lógica infinitamente, pero para nuestros propósitos basta con modificar nuestro circuito con un único inductor que tenga una inductancia, L.
Ahora tenemos un LC circuito, y esto tiene una solución analítica que aclara inmediatamente la paradoja: La corriente fluirá de un lado a otro entre los condensadores y a lo largo de los cables de longitud finita, oscilando a una frecuencia dada por: f=1/\sqrt{2\pi LC}. Nunca habrá una solución en estado estacionario, por lo que nunca podremos evaluar únicamente la energía electrostática. También tenemos que considerar la energía debida a las cargas en movimiento, es decir, el flujo de corriente, Iy ésta viene dada por W_L = \frac{1}{2} L I^2. La suma de esta energía eléctrica y magnética (\frac{1}{2} L I^2 + \frac{1}{2} C V^2) no cambiará con el tiempo.
Verificación en COMSOL Multiphysics® Software
Es sencillo construir un modelo que verifique esta situación utilizando COMSOL Multiphysics® y el módulo RF. Lo haremos utilizando el Ondas electromagnéticas transitorias junto con la interfaz Electrostática para calcular las condiciones iniciales. Modelaremos una pequeña región de vacío perfecto con los condensadores y los cables en su interior. Las placas del condensador, los cables y el espacio alrededor de nuestro volumen se tratarán como conductores eléctricos perfectos, lo que significa que los campos electromagnéticos no penetrarán a través de ningún límite. Hay una guía para configurar estos modelos de descarga capacitiva en nuestro artículo del Centro de aprendizaje: «Modelado de la descarga capacitiva».
La resolución de este modelo en el dominio del tiempo y la evaluación de la energía eléctrica y magnética total muestra el comportamiento oscilatorio esperado. También es posible particionar el dominio de modelado en diferentes regiones para evaluar la energía total en las regiones alrededor de los dos condensadores, así como en el espacio circundante. Este gráfico muestra cómo oscila la energía tanto en el espacio como en el tiempo.
Animación que muestra las corrientes en la superficie de las placas y los cables del condensador, así como el campo magnético en el espacio intermedio.
La energía eléctrica y magnética totales oscilan con el tiempo; la suma no cambia en este dispositivo sin pérdidas.
El total de la energía eléctrica y magnética en diferentes dominios muestra que la energía oscila en el tiempo y en el espacio.
Podemos observar que estas gráficas no son puramente sinusoidales en el tiempo, y debemos preguntarnos por qué es así. ¿De dónde procede este contenido de alta frecuencia, es decir, las ondulaciones de la energía en el tiempo? Surgen de la estructura. Está bastante claro que las dos placas tienen una capacitancia bien definida, pero también hay una separación de cargas debida a los cables, y toda esta estructura se asienta dentro de una cavidad cilíndrica que tiene una frecuencia de resonancia. Todas estas diversas partes del dispositivo tienen alguna contribución al comportamiento electromagnético. Cada contribución puede ser bastante pequeña, pero siempre existe cuando consideramos una estructura de tamaño finito.
Haciendo más preguntas: ¿Existen la capacitancia y la inductancia?
Ha llegado el momento de formular una pregunta más provocadora sobre este (o cualquier otro) dispositivo electromagnético: ¿Tiene capacitancia o inductancia? Hemos visto claramente que este dispositivo en particular tiene ambas. Pero, ¿y si lo modificamos añadiendo un material dieléctrico muy resistente entre las placas del condensador? Eso haría que la capacitancia fuera mucho mayor pero dejaría la inductancia sin cambios. Y si hiciéramos la capacitancia mucho mayor, ¿podríamos decir que la inductancia no importa?
En resumen: No, nunca debemos pensar que un dispositivo electrodinámico es puramente capacitivo o puramente inductivo. En un dispositivo electrodinámico siempre habrá energía eléctrica debida a la separación espacial de las cargas y energía magnética debida al movimiento de las cargas. Aunque a veces podemos construir situaciones hipotéticas en las que se puede ignorar una u otra, siempre tenemos que recordar que estamos haciendo una simplificación mental.
Además, todos los materiales reales tienen también cierta resistencia finita, por lo que, para ser más realistas, deberíamos hablar de todo como si tuviera una impedancia, y aquí es donde a veces nos metemos en más problemas. Cuando se trata de un modelo en el dominio de la frecuencia, existe una expresión muy familiar para la impedancia de un dispositivo eléctrico:
Z = R + j\omega L -j\frac{1}{\omega C}
La resistencia, R, en esta expresión es una medida de cómo la energía cinética de las cargas en movimiento, es decir, la corriente, se convierte en energía térmica.
Esta ecuación se reconoce inmediatamente como relativa a un oscilador armónico amortiguado de un solo grado de libertad, que es uno de los problemas más estudiados en ingeniería y física. Sabemos que podemos calcular a partir de esta expresión la frecuencia de resonancia y el factor de calidad de un oscilador de este tipo, y sabemos que los dispositivos reales tienen una resonancia y un factor de calidad fundamentales. Esto nos tienta a equiparar ambos e intentar reducir un dispositivo eléctrico del mundo real, de tamaño finito, a una sola resistencia, capacitancia e inductancia. Esto es un error conceptual y nunca es válido porque la expresión anterior para la impedancia sólo es aplicable a un dispositivo que tenga un tamaño infinitesimal.
Cualquier dispositivo real tiene un tamaño finito, y cuando funciona en resonancia, la energía eléctrica y magnética varían en el espacio y en el tiempo, como vimos en los gráficos anteriores. Por lo tanto, un modelo de circuito equivalente requiere al menos tres nodos al menos tres nodos, aunque a veces muchos más. Volviendo a pensar en nuestro modelo físico de los dos condensadores y suponiendo que la placa de cada condensador está representada por un nodo del circuito eléctrico, podemos ver que el modelo de circuito equivalente tendría que ser al menos tan complicado como el circuito representado a continuación, con cuatro nodos. Observe que se ha añadido una pequeña capacitancia en paralelo a la inductancia de los cables, ya que también existe una separación de carga a lo largo de los cables.
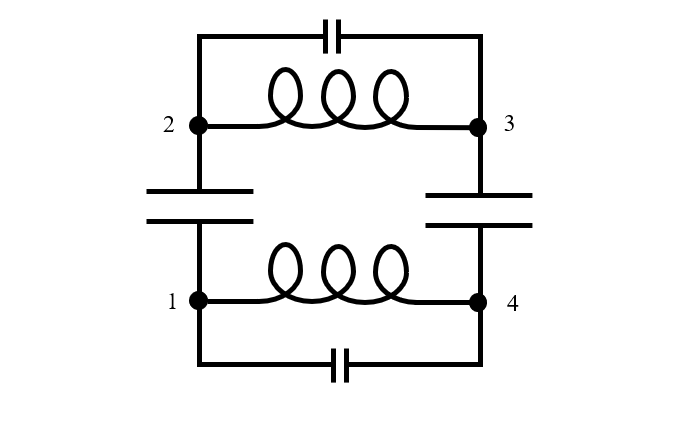
Un modelo de circuito equivalente de dos condensadores sin pérdidas de tamaño finito conectados en serie.
Es de esperar que podamos ver en este ejemplo que construir un modelo de circuito equivalente que sea válido cerca de la resonancia puede convertirse rápidamente en algo muy complicado, que requiere conocimientos físicos, un buen poco de experiencia con dispositivos similares y modelado numérico.
Volviendo a la pregunta original, se podría argumentar que la capacitancia, la inductancia e incluso la resistencia son conceptos que no existen por sí solos, que sólo existen en combinación unos con otros. Aunque a veces podemos reducir la impedancia dependiente de la frecuencia de un dispositivo a una sola resistencia, capacitancia y/o inductancia, tales simplificaciones sólo son válidas a frecuencias por debajo de la resonancia del dispositivo. Tener esto en cuenta nos ayuda a evitar todo tipo de trampas, que van desde esta entretenida paradoja de los dos condensadores hasta problemas del mundo real mucho más frustrantemente complejos.
Observaciones finales
Hemos utilizado aquí un experimento mental clásico para comprender por qué la impedancia de un dispositivo electromagnético que funciona cerca de la resonancia no puede descomponerse en una única resistencia equivalente, capacitancia e inductancia. Los experimentos mentales como la paradoja de los dos condensadores son valiosos para ampliar nuestra comprensión del electromagnetismo e interpretar los resultados de nuestros modelos computacionales.
Lecturas complementarias
¿Le interesa saber cómo se pueden utilizar el modelado y la simulación para resolver otros rompecabezas? Consulte otros ejemplos en el Blog de COMSOL:
Únase al foro de diseñadores!
Su experiencia es vital para la comunidad. Únase a nosotros y aporte sus conocimientos.
Únase ahora al ForoComparta, aprenda y crezca con los mejores profesionales del sector.


