Explicación de los momentos de inercia de masa de SOLIDWORKS

Únase al foro de diseñadores!

Su experiencia es vital para la comunidad. Únase a nosotros y aporte sus conocimientos.

Comparta, aprenda y crezca con los mejores profesionales del sector.

Todos nos hemos referido a las propiedades de masa cuando trabajamos con modelos sólidos, especialmente cuando tomamos Certificaciones SOLIDWORKS¡! En su mayor parte, la información útil está disponible de un vistazo: Densidad, Masa, Volumen, Superficie, etc. Pero, ¿cómo interpreta alguien el resto de la información incluida en Propiedades de la masa, en particular los números de la parte inferior? ¿Qué nos dicen exactamente?

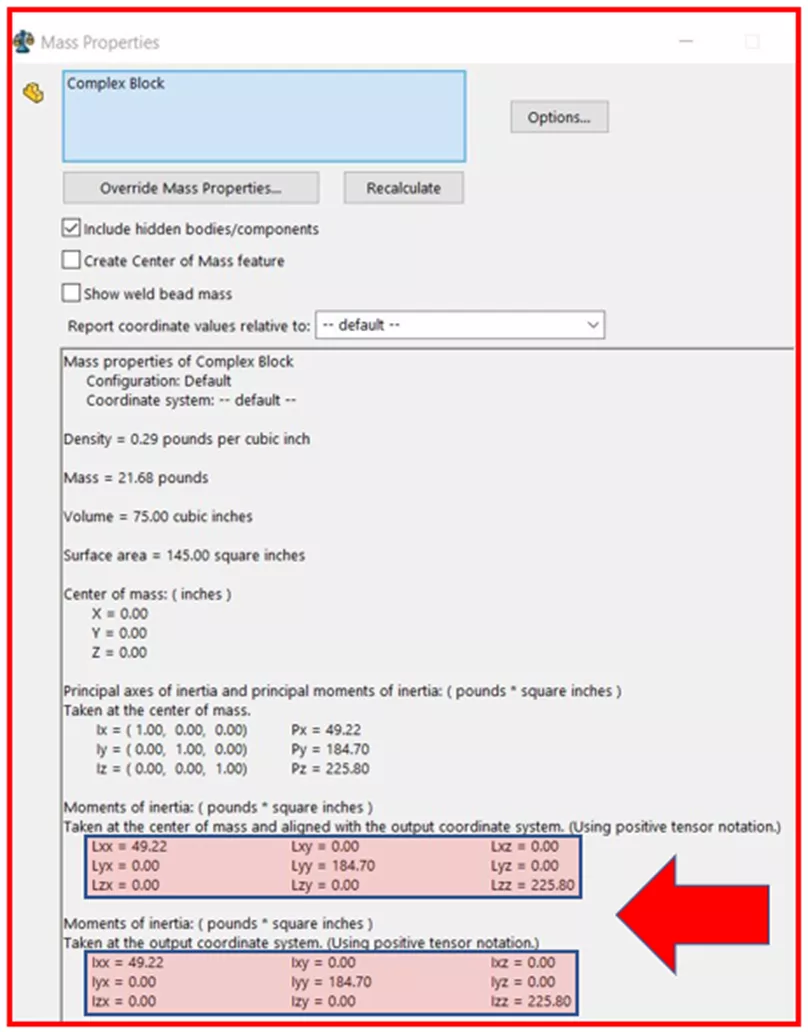
Todo se remonta a los Momentos de Inercia, que dependen de la masa, la forma y el eje de rotación.

Todo objeto tiene un Centro de Masa que, si se suspende en el aire desde este punto, estará perfectamente equilibrado. Tomando el siguiente simétrico bloque complejo como ejemplo, podemos ver los ejes principales a través de su centro de masa.

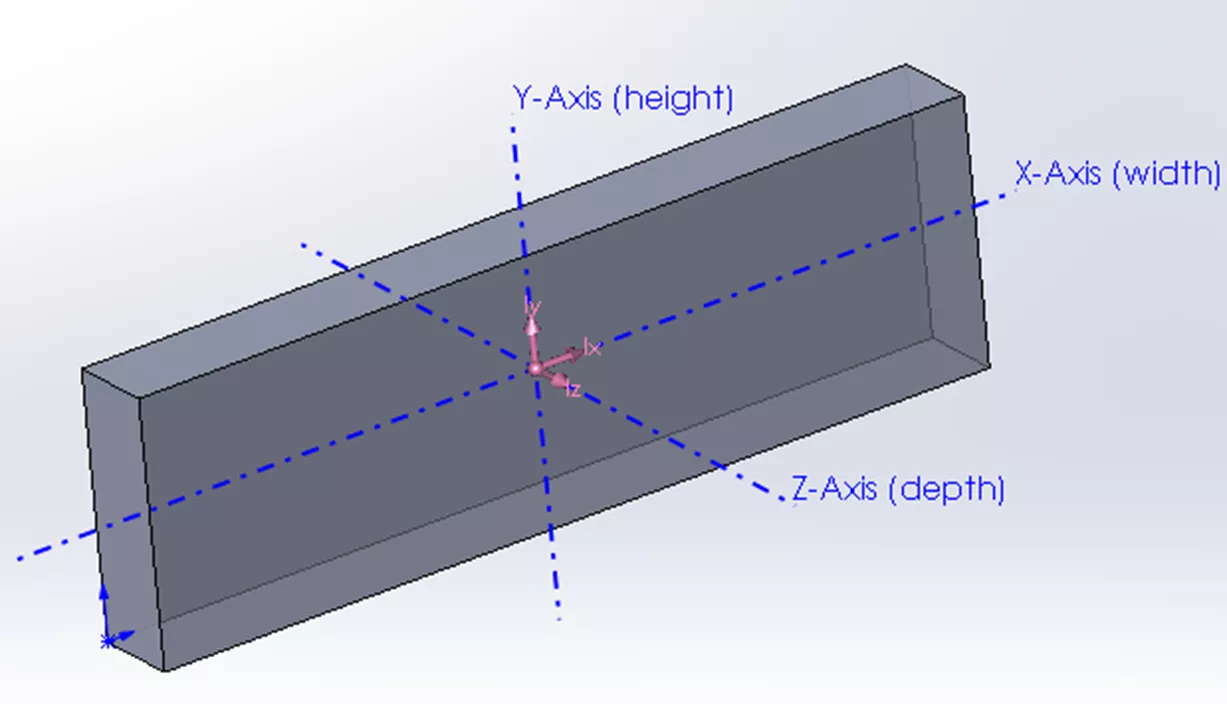
Si el bloque girara alrededor de cualquiera de estos ejes, veríamos los valores principales de masa-momento de inercia que se muestran en unidades de ML². Estos valores representan la distribución de la masa alrededor de cada eje.

Los grupos de números (matrices de 3×3) en la parte inferior de la ventana Propiedades de masa representan Tensores de inercia.

Sin ponernos demasiado técnicos, los elementos diagonales de estas matrices siempre representan Momentos de inercia de la masa en torno a los ejes primarios de un sistema de coordenadas establecido. Cualquier elemento no diagonal representa un Producto cruzado MOI. El MOI de producto cruzado es en realidad sólo una indicación de la simetría del objeto. Si es distinto de cero, entonces podemos esperar un par o aceleración fuera del eje que dará lugar a un bamboleo del objeto; no a una rotación pura. Piense en la rueda de un coche siendo equilibrada para evitar el tambaleo.

Veamos un ejemplo de un objeto que es simétrico respecto a un solo plano (XY):

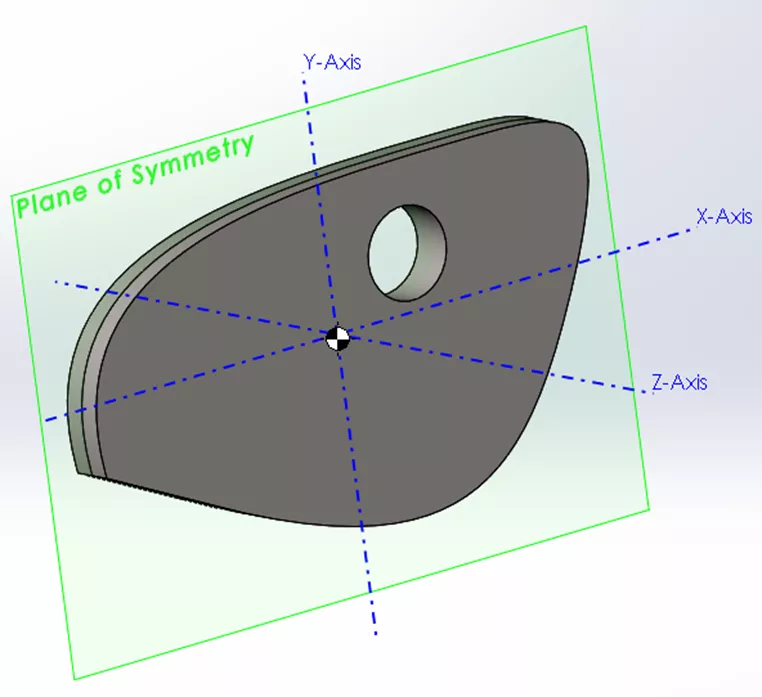
Aquí vemos valores cero para todos los productos cruzados que contienen el eje Z (no hay bamboleo en la dirección Z). Esto se debe a que la masa del objeto está equilibrada por igual a lo largo de este eje a ambos lados del plano de simetría.

Una forma de interpretar la notación matricial es la siguiente: si un objeto gira alrededor del eje X, entonces Lxx es su inercia «contra» la rotación alrededor del eje X mientras que, simultáneamente, Lxz es su inercia «contra» la rotación alrededor del eje Z.

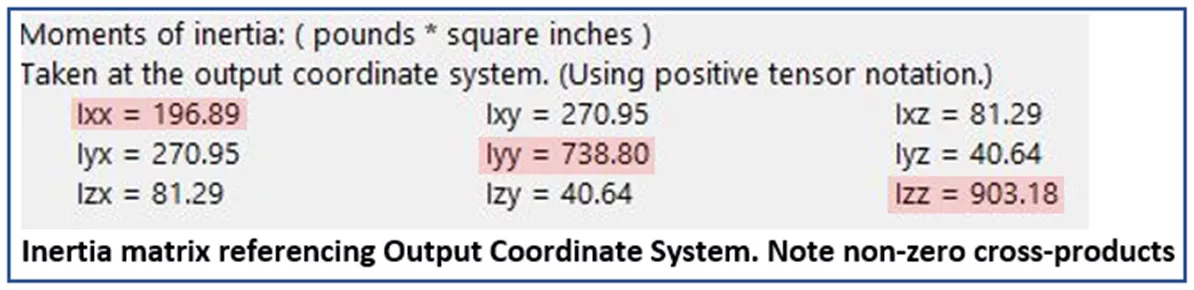
Por último, probablemente se habrá dado cuenta de que las propiedades de masa también dan valores de MOI sobre el Sistema de coordenadas de salida ejes. El OCS es el marco de referencia por defecto al iniciar una pieza, un ensamblaje, etc., por lo que su ubicación depende de cómo se construya un modelo.

En el siguiente ejemplo, el bloque se creó extruyendo hacia delante desde el origen por defecto (plano frontal), por lo que su OCS está situado en la esquina inferior trasera izquierda. Vale la pena señalar que la ubicación del sistema de coordenadas de salida puede cambiarse fácilmente incluso después de completar una pieza y se hace a través de Geometría de referencia.

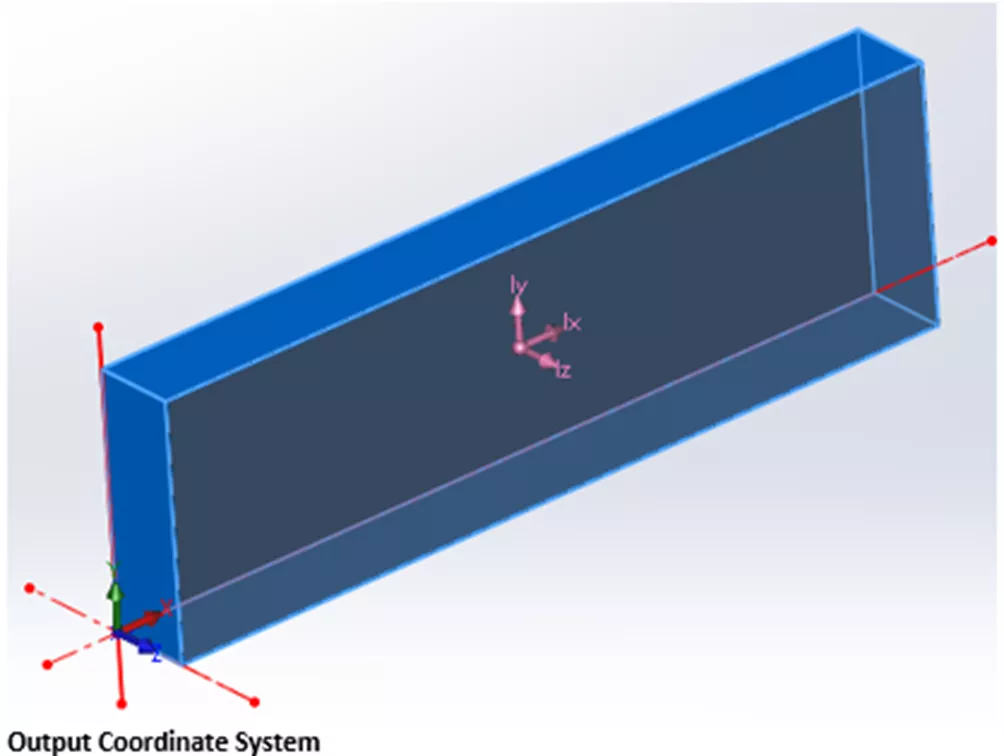
La matriz inferior de números en Masa-Propiedades se calcula haciendo referencia al Sistema de coordenadas de salida. En este caso, es fácil imaginar nuestro modelo de ejemplo girando en torno a los ejes OCS y, como cabría esperar, los momentos de inercia son mucho mayores. De nuevo, vemos los MOI sobre cada eje expresados en los elementos diagonales pero esta vez, como el modelo no es simétrico sobre ninguno de los ejes OCS, vemos valores distintos de cero en todos los productos cruzados.

Únase al foro de diseñadores!

Su experiencia es vital para la comunidad. Únase a nosotros y aporte sus conocimientos.

Comparta, aprenda y crezca con los mejores profesionales del sector.