Únase al foro de diseñadores!
Su experiencia es vital para la comunidad. Únase a nosotros y aporte sus conocimientos.
Únase ahora al ForoComparta, aprenda y crezca con los mejores profesionales del sector.
Las técnicas disponibles como controladores de adaptadores en el compositor de procesos son magníficas. Son el resultado de una profunda investigación en métodos numéricos. Las técnicas más destacadas son DOE, optimización, aproximaciones y Six-Sigma. Ya hemos hablado en detalle de DOE en blogs anteriores. En este blog vamos a profundizar en la Optimización. No olvidemos que estamos en el compositor de procesos, por lo que la optimización es paramétrica impulsada principalmente por parámetros geométricos o físicos.
La definición clásica de optimización
Usted tiene una pelota en algún lugar del campo vallado. Usted tiene un punto de partida. Tiene que encontrar la pelota recorriendo la distancia mínima sin cruzar la valla. Dispone de sensores de ayuda. La pelota es la función Objetivo. Las vallas son las restricciones. Los sensores son las técnicas de optimización utilizadas.

La diferencia entre el diseño de experimentos y la optimización
La diferencia entre ambos es la misma que existe entre «mejor» y «el mejor». El diseño de experimentos es un método para elegir el punto de diseño más adecuado de forma eficiente a partir de un conjunto de puntos existentes. Este conjunto puede ser definido por el usuario o por el propio DOE. Las técnicas de optimización comienzan con un único punto de diseño inicial y navegan iterativamente en el espacio de diseño para llegar al punto de diseño óptimo o el mejor. Dependiendo del problema, la EOD puede ser precursora de la optimización.
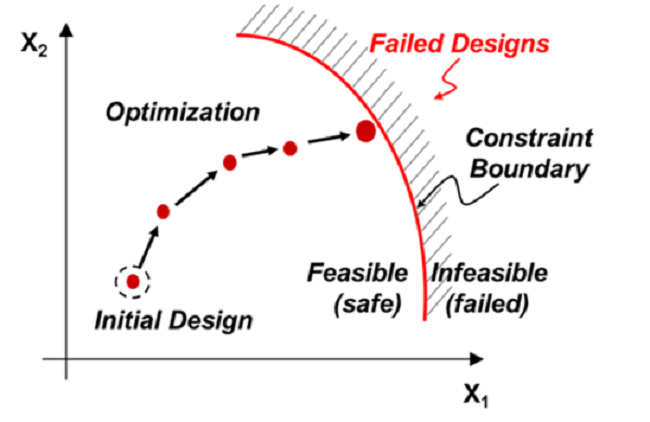
Tipos de técnicas de optimización
Existen diferentes métodos para clasificarlas dependiendo de cómo se defina la función objetivo y del tipo de espacio de diseño adecuado.
Técnicas restringidas: Utilizan funciones separadas para operar, una para el objetivo y otra para las restricciones. Todos hemos visto este tipo de técnicas a algún nivel durante los cursos de ingeniería. Son las más comunes.
Minimizar/Maximizar F(x) en x1>x>x2
Sujeto a: h(x)>a1; g(x)>a2; f(x)=0 etc.
Técnicas sin restricciones: Utilizan una sola función tanto para el objetivo como para las restricciones. El usuario sigue definiendo las restricciones por separado del objetivo, pero internamente el problema con restricciones se convierte en un problema sin restricciones.
En función de la aplicación a distintos tipos de espacio de diseño, los métodos de optimización pueden clasificarse en basados en el gradiente, directos o exploratorios. Las abreviaturas que aparecen en las imágenes de abajo son los nombres de los métodos de las categorías respectivas.
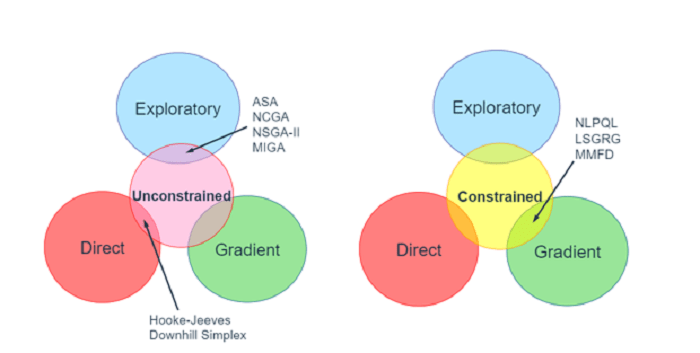
Métodos de gradiente: Son los más antiguos y han sido bien probados en la industria. Funcionan según el principio de mínima energía o máxima estabilidad. Si deja caer suavemente una bola en un valle, se deslizará por el camino de mayor pendiente hasta alcanzar el punto más bajo de sus proximidades. Estos métodos funcionan en un espacio de diseño continuo que tiene continuidad C0 y C1. Es probable que se queden atascados en los mínimos locales, por lo que el punto inicial debe elegirse con cuidado.

Métodos directos: Un algoritmo de búsqueda directa comienza con un punto base. Busca un conjunto de puntos a su alrededor buscando uno en el que el valor de la función objetivo sea inferior al actual. El algoritmo salta a ese punto como nuevo punto base y busca un nuevo conjunto de puntos a su alrededor. Se puede deducir que este método es eficiente desde el punto de vista computacional, ya que no requiere el cálculo del gradiente. Es más versátil ya que no se requiere continuidad C0 y C1. Los más comunes son Hooke’s-Jeeves y Downhill Simplex.
El método de Hooke’s Jeeves no pierde de vista su dirección de desplazamiento. No cambia su dirección a cada paso si existe un punto más bajo en la dirección de desplazamiento.

Métodos exploratorios: Estos métodos se basan en técnicas de cruce o mutación entre un conjunto de datos de puntos denominados padres para generar otro conjunto de datos de puntos denominados hijos. El nuevo conjunto de datos evoluciona con cada mutación y se acerca a la solución óptima. Se trata de un esquema de alta fidelidad que funciona con todo tipo de funciones objetivo: discontinuas, no diferenciables, estocásticas, de tipo entero mixto y altamente no lineales con múltiples picos y valles, como se muestra a continuación. Sin embargo, es el esquema de optimización más caro en términos de gasto computacional. Los métodos más comunes son el algoritmo genético, el enjambre de partículas y el recocido simulado adaptativo.
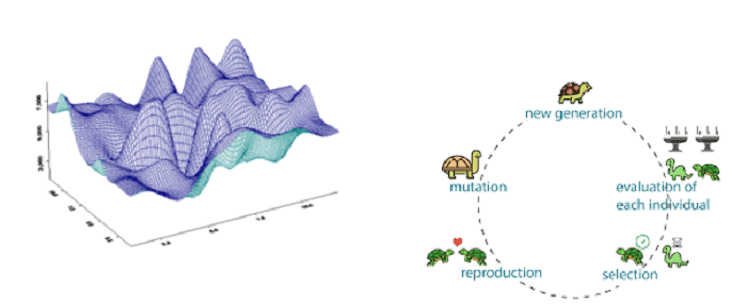
Métodos basados en punteros: Se trata de un enfoque de mezcla y combinación en caso de que el usuario no tenga ni idea de qué tipo de técnica sería la más adecuada para resolver el problema con una precisión razonable. El enfoque del puntero puede ayudar cuando el usuario se encuentra con un tipo de espacio de diseño desconocido y difícil de visualizar. El método del puntero puede utilizar hasta tres esquemas de optimización, preferiblemente uno de cada cesta: gradiente, directo y exploratorio. A medida que avanza la optimización, el algoritmo rastrea la eficacia de cada método y utiliza el más apropiado para el problema dado.
Únase al foro de diseñadores!
Su experiencia es vital para la comunidad. Únase a nosotros y aporte sus conocimientos.
Únase ahora al ForoComparta, aprenda y crezca con los mejores profesionales del sector.

