Modelado de la generación de energía acústica en motores termoacústicos

Únase al foro de diseñadores!

Su experiencia es vital para la comunidad. Únase a nosotros y aporte sus conocimientos.

Comparta, aprenda y crezca con los mejores profesionales del sector.

Los motores termoacústicos generan energía acústica a partir de un aporte térmico. A diferencia de los motores de uso común, como los motores alternativos y las turbinas de gas, los motores termoacústicos no utilizan piezas móviles, lo que hace que su estructura sea muy sencilla. En esta entrada del blog, veremos cómo pueden modelarse los mecanismos de funcionamiento de los motores termoacústicos con el Acústica termoviscosa una de las potentes interfaces de COMSOL Multiphysics^® software para modelar el comportamiento linealizado de un fluido.

Cómo funcionan los motores termoacústicos

Hace más de 150 años, el profesor Pieter Rijke informó de un interesante fenómeno que puede considerarse un trabajo pionero en termoacústica. Colocó una gasa de alambre en un tubo cilíndrico de vidrio, sostenido verticalmente, y calentó la gasa por la parte inferior utilizando fuego. Tras apagar el fuego, observó que el cilindro seguía produciendo sonido durante un tiempo. (Ref. 1) El aparato es ahora bien conocido como el Tubo de Rijke, por lo que algunos habrán visto que se utiliza como ejemplo de fenómeno resonante. Sin embargo, dejando a un lado la resonancia, ¿cómo se generan los sonidos en primer lugar?

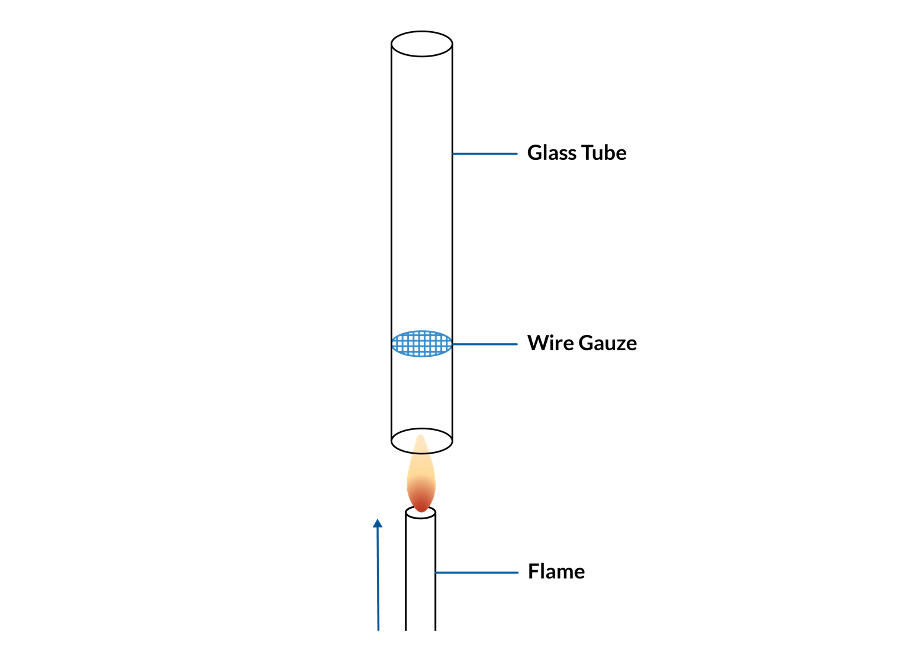
El montaje del tubo de Rijke.

El truco está en la interacción entre el cambio de temperatura y el movimiento del fluido en el interior del tubo: La malla metálica calentada induce la convección natural del aire, haciendo que fluya de forma constante a través del tubo; así, el aire por encima de la malla metálica está más caliente que el aire por debajo de la malla metálica. En la resonancia acústica de media onda estacionaria en la tubería, el aire fluirá a través de la tela metálica en ambas direcciones en diferentes momentos del periodo acústico. A medida que el aire fluya a través de la gasa, se calentará. Dado que el aire por debajo de la gasa es más frío que el aire por encima, se transferirá más calor cuando el flujo sea ascendente en lugar de descendente. Para obtener un campo acústico sostenido, la liberación de calor tiene que estar en fase con el campo de presión, de forma que el fluido se caliente cuando la presión acústica sea positiva. En una onda estacionaria, el campo de velocidad, que provoca el calentamiento, está desfasado con el campo de presión. Sin embargo, debido a los efectos causados por las capas límite viscosas que rodean la malla metálica, la liberación de calor se retrasa con respecto al campo de velocidad. Este retraso de fase hace que la liberación de calor esté parcialmente en fase con el campo de presión y da lugar a una resonancia sostenida. Si el tubo se gira hacia un lado, la convección se detiene y la resonancia deja de ser sostenida. Si el tubo se gira al revés, el calor transferido será mayor cuando la presión acústica sea negativa y, por tanto, el campo acústico se atenuará en lugar de mantenerse.

Este es un ejemplo de la conversión energética entre calor y energía acústica. De hecho, todo el aparato demuestra los principios de funcionamiento de los motores termoacústicos.

Los motores termoacústicos tienen un pasaje cerrado en forma de tubo en el que puede propagarse un sonido, y en el pasaje hay un intercambiador de calor para calentar o enfriar el fluido de trabajo. Los motores termoacústicos utilizan ondas estacionarias u ondas viajeras, mientras que el tubo de Rijke sólo utiliza ondas estacionarias. Se espera que los motores de ondas viajeras obtengan un mejor rendimiento en comparación con los de ondas estacionarias debido al retardo de fase entre la presión y el desplazamiento del fluido. En esta entrada del blog, nos ocuparemos principalmente de los modelos de motores de ondas viajeras.

Pensemos en los principios de los motores termoacústicos que utilizan ondas viajeras. Para entender cómo funciona la onda, observe el movimiento de las pequeñas parcelas de fluido en la figura siguiente. Las ondas sonoras son ondas longitudinales, por lo que si una onda viajera de alta presión viene de la izquierda, los paquetes son empujados hacia la derecha. Del mismo modo, cuando una onda de baja presión procedente de la izquierda alcanza una parcela de fluido, la parcela es empujada hacia la izquierda.

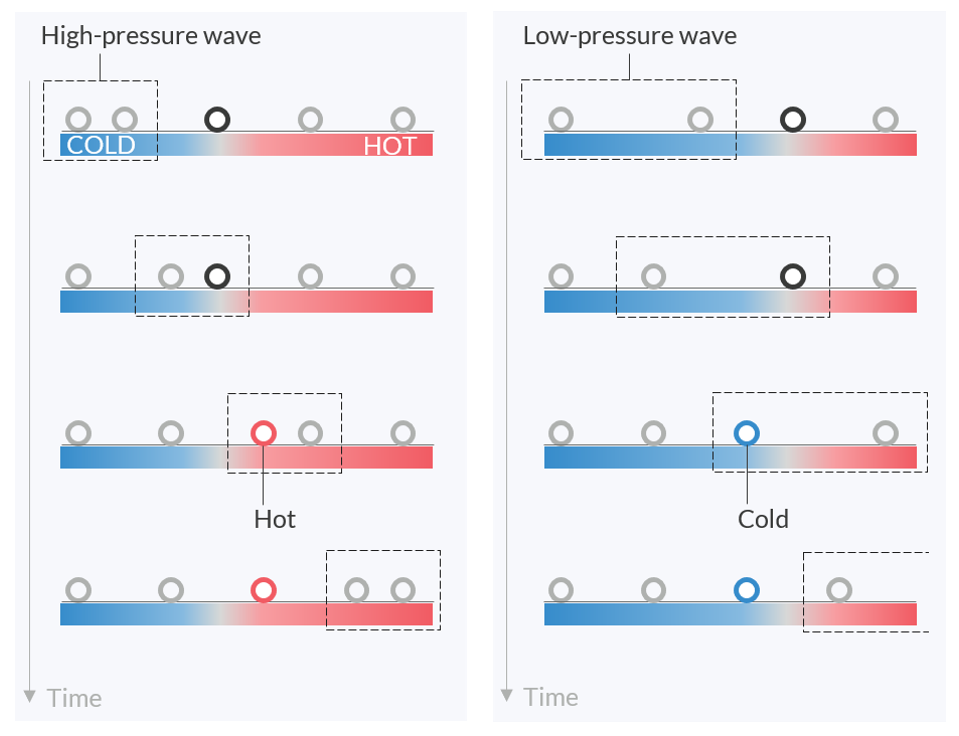
Cómo se mueven los paquetes en un fluido bajo una onda viajera procedente de la izquierda. Un área imaginaria de la onda está representada por un recuadro punteado. Con un gradiente de temperatura adecuado en la placa vecina, el paquete siempre se moverá hacia la zona más caliente si es empujado por una onda de alta presión y se desplazará hacia la zona más fría si es arrastrado por una onda de baja presión.

A continuación, considere la posibilidad de colocar una placa calentada en el tubo a lo largo de la trayectoria de la onda. Si el extremo derecho de la placa se calienta mientras que el izquierdo se mantiene a temperatura moderada, se producirá un gradiente de temperatura en la placa. El gradiente de temperatura calienta los paquetes cuando éstos se desplazan hacia la derecha, y les absorbe calor cuando se desplazan hacia la izquierda. Como una parcela tiene su máxima presión cuando se desplaza hacia la derecha, el calentamiento de la parcela empuja hacia arriba el valor máximo de la presión. Del mismo modo, la absorción de calor cuando una parcela se desplaza hacia la izquierda disminuye también la presión mínima. Esas subidas y bajadas periódicas de la temperatura sincronizan el movimiento de las parcelas y finalmente aumentan la amplitud de la onda. Todas las parcelas trabajan juntas como una cadena para transportar la onda de presión y añadir una energía a la onda mediante el intercambio de calor. Tenga en cuenta que el gradiente de temperatura en la placa debe estar en la misma dirección que la propagación de la onda, de lo contrario la onda simplemente se atenuará.

Si se pregunta si existe un dispositivo con un ciclo invertido del motor, la respuesta es sí, existe. Este sistema se denomina bomba de calor termoacústica o refrigerador termoacústico, y puede desplazar el calor mediante ondas acústicas. El principio de funcionamiento es sencillo: Cuando una onda de alta presión llega a un paquete, éste se comprime, la temperatura aumenta en consecuencia y el paquete empieza a disipar su calor al objeto vecino mientras se desplaza hacia la derecha. A la inversa, con una onda de baja presión, un paquete absorbe calor y se desplaza hacia la izquierda.

La explicación aquí expuesta sólo tiene fines introductorios y no contiene todos los detalles de los motores termoacústicos. Si está interesado en una información más detallada sobre los motores termoacústicos, consulte la Ref. 2.

Ecuaciones linealizadas para el modelado termoacústico

Siempre es importante pensar qué conjunto de ecuaciones y qué interfaz son adecuados para una nueva simulación. Para el presente ejemplo de modelado, puede parecer razonable utilizar el módulo de acústica para simular la oscilación termoacústica, ya que el fenómeno está relacionado con las ondas acústicas. Además, dado que el ámbito académico se denomina termoacústica, el Acústica termoviscosa parece ser una buena elección. Comprobemos las ecuaciones y la capacidad de esta interfaz para validar nuestra elección.

El Acústica termoviscosa utiliza las siguientes ecuaciones en un análisis en el dominio del tiempo:

\frac{{parcial \rho_{\rm t}}{parcial t}+\nabla\cdot (\rho_0 \bm{u}_{\rm t}) = 0 \\

\rho_0\frac{{parcial \bm{u}_{\rm t}}{{parcial t} = \nabla\cdot{\bm{\sigma}{\i}

\rho_0C_p\left(\frac{{parcial T_{\rm t}}{parcial t} + \bm{u}_{\rm t}\cdot\nabla T_0\\right)-\alpha_pT_0\left(\frac{{parcial p_{\rm t}}{parcial t} + \bm{u}_{rm t}\cdot\nabla p_0\rm t) = \nabla\cdot(k\nabla T_{\rm t})+Q,

donde \rho, \bm{u}, Ty p son densidad, velocidad, temperatura y presión, respectivamente. El subíndice {\cdot}_0 expresa que el valor pertenece al flujo medio de fondo, mientras que las variables con el subíndice {\cdot}_t representan las perturbaciones acústicas. Las ecuaciones gobernantes del Acústica termoviscosa se derivan de las ecuaciones de Navier-Stokes (las ecuaciones exactas del movimiento de los fluidos) basándose en la suposición de que cada término de perturbación de segundo orden puede omitirse en la simulación y que la velocidad del flujo medio de fondo es cero (\bm{u}_0=\bm{0}).

Debemos prestar atención a las no linealidades despreciadas y a si las ecuaciones linealizadas cubren el fenómeno de nuestro interés. En el caso de los motores termoacústicos, el intercambio de calor entre un fluido y un intercambiador se expresa mediante el término de difusión \nabla \cdot (k\nabla T_{\rm t}), y la transferencia de calor debida a la oscilación acústica se expresa mediante el término de advección linealizado \bm{u}_{\rm t}\cdot \nabla T_0. Un fluido frío con una alta presión advectada por el término \bm{u}_{\rm t}\cdot \nabla T_0 se calienta en un intercambiador de calor por \nabla \cdot (k\nabla T_{\rm t}), y la energía se incrementa a través de la tercera ecuación. Estos términos describen los mecanismos importantes de transferencia de calor en nuestro sistema y, por lo tanto, las ecuaciones linealizadas parecen ajustarse bien al modelado del motor.

Obsérvese también que no hay ningún término de advección que represente el acoplamiento del campo de temperatura variable en el tiempo y la velocidad de oscilación, \bm{u}_{\rm t}\cdot\nabla T_t. Esta representación acoplada mostraría el transporte inducido por la oscilación del campo de temperatura transitorio. El término de advección es importante para la simulación de las bombas de calor, donde el gradiente de temperatura en equilibrio se determina como resultado de las oscilaciones y no está disponible a priori. En tales casos, podemos utilizar la característica Contribuciones de la acústica termoviscosa no lineal, que permite al modelo tener en cuenta los términos no lineales en la Acústica termoviscosa, transitoria interfaz. La simulación de las no linealidades puede ser costosa, por lo que la funcionalidad no lineal sólo debe añadirse en los dominios relevantes.

Modelado en COMSOL Multiphysics^®

Hasta ahora, hemos cubierto los mecanismos básicos de funcionamiento de los motores termoacústicos y las ecuaciones gobernantes relevantes para modelarlos, así que pasemos a la construcción del modelo. Puede acceder a los archivos del modelo para los ejemplos mostrados aquí en la Galería de aplicaciones. Como se ha comentado en la sección anterior, utilizaremos el modelo Acústica termoviscosa para modelar motores termoacústicos de ondas viajeras. Dado que el campo de temperatura de fondo estacionario no es uniforme, la Transferencia de calor también se utiliza la interfaz. En lugar de utilizar las dos interfaces simultáneamente, todo el estudio puede dividirse en dos pasos: a Estacionario para el campo de temperatura de fondo y un Dependiente del tiempo para los campos acústicos. El acoplamiento se realiza simplemente fijando la solución del Transferencia de calor como la temperatura de equilibrio en la Modelo acústico termoviscoso nodo.

En cuanto a las condiciones límite del Acústica termoviscosa interfaz, debemos ajustar la pared del intercambiador de calor para que sea isotérmica (T_{\rm t} = 0). Esta condición calienta la temperatura del fluido con una presión elevada (donde T_{\rm t} es menor que cero debido a la advección desde la zona más fría) y enfría el fluido cuando su presión es baja (donde T_{\rm t} es superior a cero).

Ejemplo 1: Bucle simple

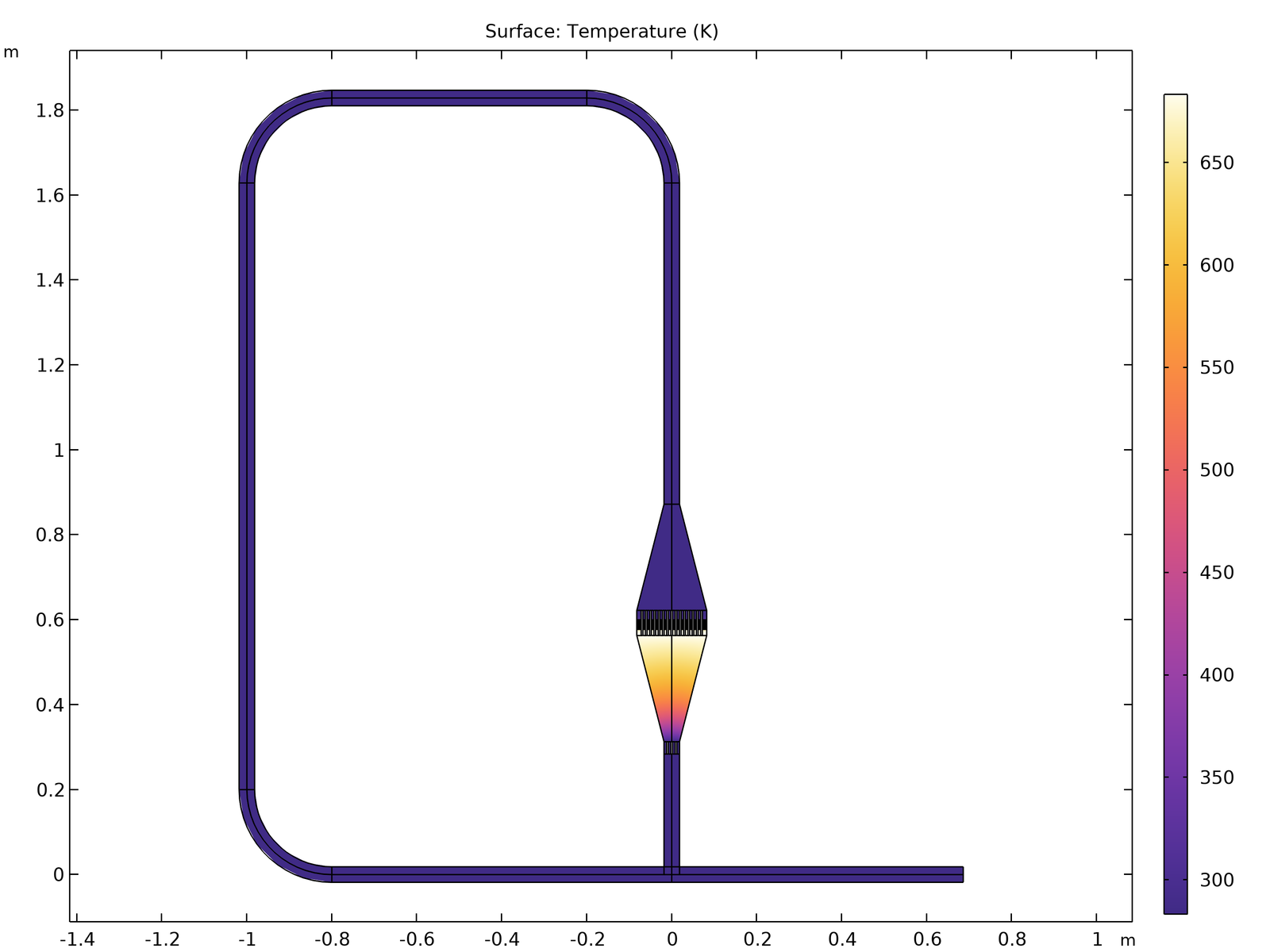
En primer lugar, modelaremos un motor formado por un bucle simple. Tiene un intercambiador de calor en el paso derecho, y todo el paso forma un circuito cerrado. La temperatura estacionaria aparecerá como se muestra en la siguiente figura. El gradiente de temperatura en la región inferior del intercambiador de calor puede ser llamativo, pero nuestro interés se centra en el gradiente de temperatura en los pequeños huecos del intercambiador de calor.

La temperatura de equilibrio en un motor simple tipo bucle (izquierda: sistema completo; derecha: primer plano alrededor del intercambiador de calor). El extremo inferior de los estrechos conductos de un intercambiador de calor se calienta a 493 K.

En el En función del tiempo paso de estudio, se da una onda estacionaria como condición inicial de la presión para que pueda desencadenar la oscilación dentro del bucle. A medida que prosigue la simulación, la amplitud crece, como lo capta el Sonda puntual (que se muestra a continuación). Es evidente que la oscilación sigue creciendo, lo que significa que la energía térmica se convierte en energía acústica.

El Sonda puntual está configurada para realizar un seguimiento de la presión en el motor. Los datos de presión se toman en un punto del intercambiador de calor cercano al nodo de presión de la onda estacionaria utilizada como distribución inicial de la presión.

Entonces, ¿cómo es la presión en el motor? Las tres figuras siguientes visualizan la distribución de presión en t = 0,281 s, 0,285 s y 0,289 s, respectivamente. Se da una onda estacionaria en t = 0 s, pero tras un breve periodo, la distribución empieza a girar en el sentido de las agujas del reloj. La onda viaja en la misma dirección que el gradiente de temperatura en el intercambiador de calor, y el componente antihorario de la onda estacionaria inicial se atenúa debido a la falta de suministro de energía para ella. Curiosamente, la excitación de una onda en sentido contrario a las agujas del reloj puede simularse invirtiendo la dirección del gradiente de temperatura en mitad de la simulación. En el archivo del modelo, el Estacionario se calcula de nuevo con el perfil de temperatura invertido en t = 0,3 s, y la Dependiente del tiempo refleja el cambio de la temperatura de equilibrio desde entonces. La onda en el sentido de las agujas del reloj se mantiene hasta aproximadamente t = 0,6 s. Posteriormente, aparece una distribución similar a una onda estacionaria en el motor, y la onda se propaga finalmente en sentido contrario a las agujas del reloj.

Historia de la distribución de la presión (izquierda: t = 0,281 s; centro: t = 0,285 s; derecha: t = 0,289 s). Tanto la zona de alta presión como la de baja presión se mueven en el sentido de las agujas del reloj debido al efecto termoacústico comentado anteriormente.

Ejemplo 2: Bucle con un muñón

Además del bucle simple, comprobaremos una configuración más. La siguiente figura muestra el siguiente ejemplo de modelo con una geometría compleja. La geometría imita la configuración experimental de la Ref. 3. El modelo es 2D y se ha simplificado para que tenga el mismo diámetro hidráulico que el intercambiador de calor analizado en la referencia. La tubería ramificada (denominada stub) en el extremo inferior derecho se añade para la futura extracción de la energía acústica. Como en el ejemplo 1, el bucle se utiliza en el motor para convertir la energía térmica en energía acústica, pero aquí, una parte de la energía puede extraerse en el stub.

La temperatura de equilibrio en un modelo con un stub. La geometría imita el montaje experimental de la Ref. 3.

Las distribuciones instantáneas de presión en el motor se muestran en la siguiente figura. Hay una caída brusca donde la longitud del arco es igual a 3,6 m, causada por el arrastre viscoso en los pequeños huecos del intercambiador de calor. Cabe destacar que la amplitud de la presión depende en gran medida de la posición. Esto se debe a la complejidad del modelo, como el arrastre viscoso y una componente de onda estacionaria sostenida en el motor. En la figura, el valor máximo temporal de la presión absoluta, etiquetado como max(|p|), también se traza en cada posición. Observe que, aunque la amplitud parece un poco grande, esta simulación supone que no hay turbulencias y que cualquier perturbación es lineal. Cuando se adimensionaliza con su máximo espacial, la distribución de la amplitud aproximada, max(|p|), concuerda bien con los datos experimentales y analíticos de la Ref. 3.

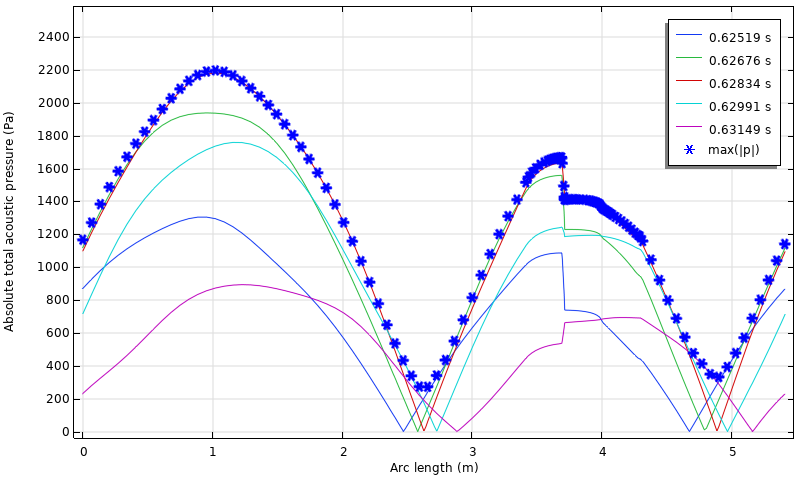
Distribuciones instantáneas de presión a lo largo del bucle y la amplitud aproximada, max(|p|)calculado por una variable de estado.

Vea otros ejemplos

Desde la demostración del profesor Rijke, se ha producido un crecimiento significativo en la comprensión de la termoacústica, y actualmente se estudia activamente su aplicación en dispositivos energéticos. En esta entrada del blog, cubrimos cómo se pueden modelar los motores termoacústicos utilizando el Acústica termoviscosa y se visualizaron las interesantes características de los motores.

En la Galería de aplicaciones, encontrará muchos modelos de distintas disciplinas físicas. Dos de los modelos relacionados con la termoacústica son:

• Motor termoacústico simple, que es un modelo de un motor termoacústico de onda estacionaria. Hay varios archivos de modelo, que ofrecen una comparación de la configuración del mismo modelo con dos enfoques diferentes: un enfoque de perturbación lineal por el Acústica termoviscosa, transitoria y un enfoque no lineal completo por el Flujo no isotérmico interfaz multifísica. Este último enfoque resuelve las ecuaciones de Navier-Stokes y tiene en cuenta la no linealidad a costa de un mayor tiempo de cálculo.
• Motor termoacústico y bomba de calor, que es un modelo de bomba de calor de onda estacionaria. A diferencia de los motores termoacústicos, la simulación de las bombas de calor termoacústicas requiere el cálculo del término de advección no lineal \bm{u_t}\cdot\nabla T_{\rm t} porque la temperatura seguirá disminuyendo debido al efecto de transporte térmico. En el modelo, la Contribuciones de la acústica termoviscosa no lineal se añade el nodo Acústica termoviscosa para tener en cuenta la no linealidad. El modelo también utiliza la Perturbación acústico-térmica termoviscosa Límite acoplamiento, una novedad de la versión 6.2. El acoplamiento se utiliza para simular el intercambio de calor entre el fluido oscilante y las placas sólidas del paso, ya que la temperatura del sólido sigue disminuyendo en función del bombeo del calor.

Referencias

1. P.L. Rijke, «LXXI. Aviso sobre un nuevo método para provocar la vibración del aire contenido en un tubo abierto por ambos extremos». Revista filosófica y científica de Londres, Edimburgo y Dublín, vol. 17, nº 116, 419-422, 1859; https://doi.org/10.1080/14786445908642701
2. G.W. Swift, Termoacústica: Una perspectiva unificadora para algunos motores y refrigeradores, Springer, 2017; https://doi.org/10.1007/978-3-319-66933-5
3. M. McGaughy y otros, «A Traveling Wave Thermoacoustic Engine-Design and Test,» Cartas Dyn. Sys. Control, vol. 1, no. 3, julio de 2021; https://doi.org/10.1115/1.4049528

Únase al foro de diseñadores!

Su experiencia es vital para la comunidad. Únase a nosotros y aporte sus conocimientos.

Comparta, aprenda y crezca con los mejores profesionales del sector.