Rejoignez le forum des designers !
Votre expertise est essentielle pour la communauté. Rejoignez-nous et apportez vos connaissances !
Rejoindre le forum maintenantPartagez, apprenez et évoluez avec les meilleurs professionnels du secteur.
Résumé
Dans la première partie de cette série de discussions, j’explore et je vérifie la relation entre les calculs manuels et la réponse en fonction du temps d’un objet qui tombe sur une surface rigide, ainsi que les déviations et les contraintes qui se produisent pendant la période d’impact. Les concepts discutés ci-dessous sont impératifs pour comprendre comment configurer et résoudre une analyse structurelle transitoire à l’aide d’ANSYS Mechanical.
Figure 1 : Barre pendant l’impact (avec une échelle de déviation exagérée).
La figure 1 illustre notre exemple de barre après sa chute et montre ce qui se passe pendant la période d’impact. Le reste du document explore la manière dont nous pouvons configurer et analyser ce type de système et comparer nos progrès avec les calculs manuels courants.
Voici une liste des sujets abordés dans cette discussion (par ordre d’apparition) :
- Énergie potentielle
- Énergie élastique
- Rigidité directionnelle
- Analyse statique des structures
- Force de compression moyenne
- Énergie cinétique
- Vitesse d’impact
- Période d’impact
- Fréquence naturelle
- Masse effective modale
- Analyse structurelle transitoire
- Durée de l’analyse
- Pas de temps Fréquence
- Résultats des déplacements et des contraintes transitoires complexes
- Contrainte de compression moyenne
Détails
J’ai commencé à explorer la relation entre les calculs manuels et les résultats de déformation et de contrainte maximales produits par des événements dynamiques, tels que l’impact d’un objet sur un autre. J’ai utilisé ANSYS Mechanical pour vérifier les hypothèses et obtenir plus de détails sur ces événements dynamiques. J’ai confiance dans la méthode des éléments finis et j’ai hâte de partager mes découvertes avec vous.
J’ai commencé mon exploration par un exemple simple d’une barre cylindrique tombant sur une surface rigide. Dans ce scénario, et dans tous les scénarios associés à cette discussion, je suppose que le matériau a un comportement élastique et qu’aucune des charges ne provoque de plasticité ou de dommages. Cela signifie qu’il y a conservation de l’énergie dans la géométrie.
Au cours de ce processus, j’ai formulé une série d’hypothèses et effectué des analyses par éléments finis pour vérifier ou contester ces hypothèses. Ce processus m’a amené à poser plus de questions, à analyser et à obtenir plus de réponses. Au final, je suis en mesure de décrire avec confiance de nombreux aspects de cet événement dynamique, que je présenterai de la manière la plus concise possible.
Commençons par l’idée la plus simple.
Ce premier exemple explore la chute d’une barre cylindrique sur une surface dure. La barre a un diamètre de 25,4 mm, une longueur de 254 mm et une densité de masse de 7,85e-06. [kg/mm³]. Cette barre sera lâchée à 1 mètre de la face inférieure.
Figure 2 : Barre cylindrique
Dans ces conditions, l’énergie potentielle doit être égale à l’énergie élastique.
Énergie potentielle :

Énergie élastique :

Mettons en équation l’énergie potentielle de notre cylindre en chute et son énergie élastique pour savoir si nous pouvons prédire les déviations avec précision.
Supposons que la barre soit lâchée de telle sorte qu’elle se déplace dans la direction Y négative. La première étape consiste donc à déterminer la rigidité de notre géométrie dans la direction des Y.
Pour notre modèle, cette rigidité peut être calculée théoriquement, ainsi qu’en utilisant la méthode des éléments finis qui consiste à appliquer une charge connue et à diviser cette charge par la déflexion calculée dans la direction Y. Cela nous permettra de comparer les résultats obtenus avec ceux de la méthode des éléments finis. Cela nous permettra de comparer les résultats de notre estimation par éléments finis à la valeur dérivée théoriquement et de développer la confiance dans notre méthodologie.
Calculons notre rigidité théorique. Pour la direction Y, la formule suivante s’applique :

Maintenant, calculons également la rigidité géométrique par le biais d’une analyse par éléments finis selon deux méthodes différentes, afin de comprendre les différentes considérations liées aux différents types de charges.
Nous considérons ici une base fixe tout en appliquant une force à l’extrémité distale de notre cylindre de telle sorte que la force de réaction à la base soit égale en magnitude et opposée en signe à la force appliquée sur le dessus du cylindre. L’ampleur de cette charge de compression n’est pas critique, tant que les propriétés de nos matériaux sont linéaires et que nous ne considérons pas la non-linéarité de la géométrie (grandes déformations).
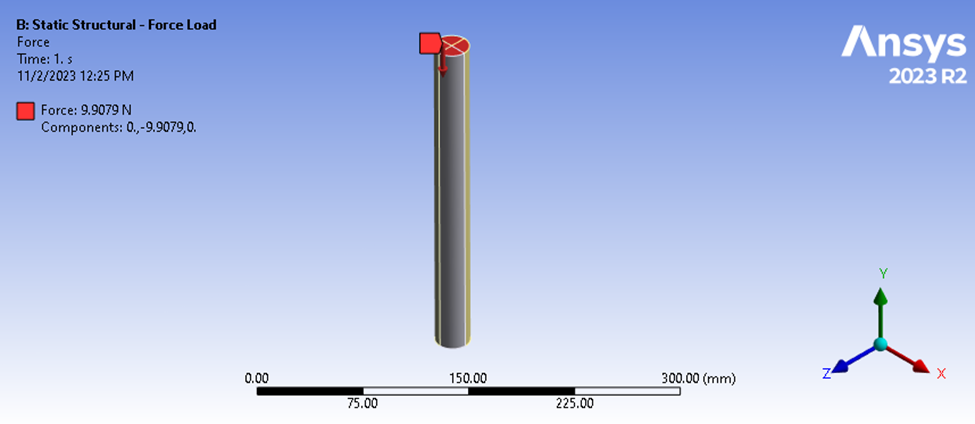
Figure 3 : Analyse structurelle statique de la tige chargée par le haut et soutenue par le bas.
Dans ce scénario, une charge de 9,9079 N est appliquée à la surface supérieure tandis que la surface inférieure est fixée à partir des déplacements en Y. L’ampleur de cette charge apparaîtra plus clairement par la suite. L’ampleur de cette charge apparaîtra plus clairement par la suite.
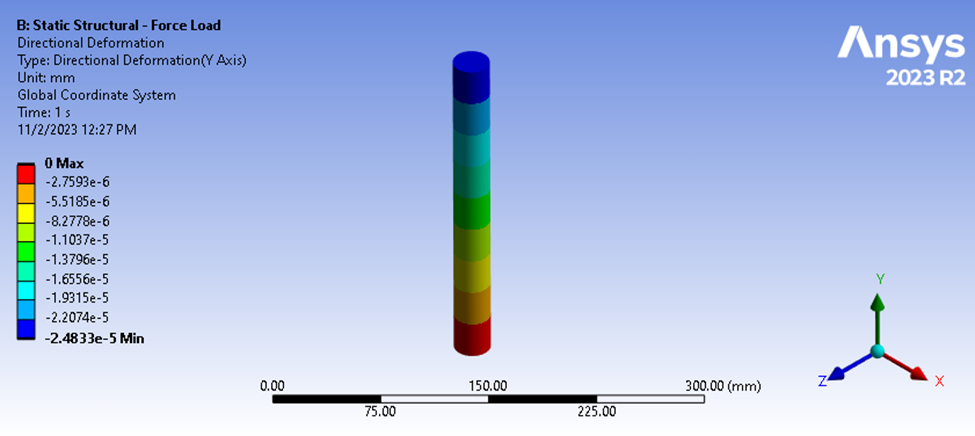
Figure 4 : Résultats de la déflexion statique de la structure
La résolution de l’analyse structurelle statique montre que l’amplitude maximale de notre déviation en compression est de 2,4833e-5 mm. Sur la base de notre charge de 9,9079 N, nous pouvons calculer la rigidité moyenne suivante.
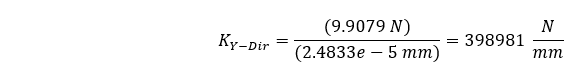
On peut voir que l’approche par éléments finis ne présente qu’une différence de 0,00125 % par rapport à l’approche théorique. Cela nous donne bonne conscience 😊
Considérons ensuite un autre type de chargement, tel que le chargement par gravité. Ici, la force est retirée de la surface supérieure, mais la surface inférieure reste contrainte, et la gravité est appliquée à 9806,6 mm/sec^2. La force de réaction à la base est de 9,9079 N, mais la force agissant sur la surface supérieure est certainement nulle. Les résultats de la déflexion montrent une magnitude de déflexion différente de 1,2421e-5 mm.
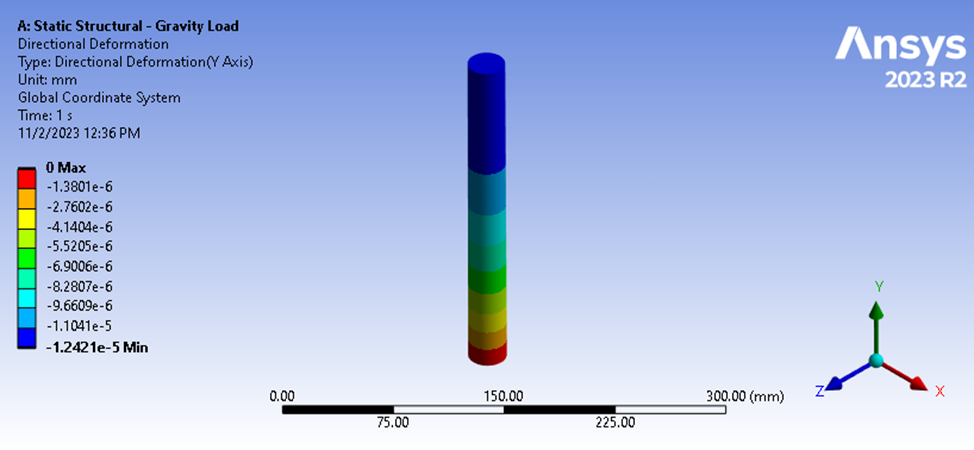
Figure 5 : Résultats de la déflexion de l’analyse structurelle statique
Si nous essayons de calculer la rigidité en utilisant la même forme d’équation que ci-dessus, nous obtiendrons une valeur incorrecte car nous ne tiendrons pas compte de la force de compression moyenne agissant sur notre géométrie. Dans ce cas, notre force de compression moyenne peut être facilement estimée puisque notre géométrie a une section transversale constante et notre rigidité moyenne estimée peut être calculée comme suit.
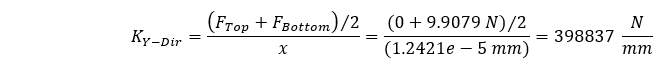
Cette estimation montre une différence de 0,0348 % par rapport à la valeur calculée théoriquement. Par conséquent, grâce à deux méthodes de chargement différentes, nous pouvons estimer en toute confiance la rigidité de la direction de la géométrie.
En substituant la rigidité directionnelle estimée à notre modèle et aux propriétés des matériaux, nous pouvons estimer la déflexion maximale ci-dessous.
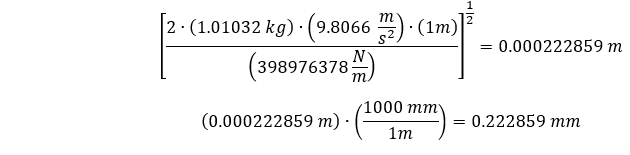
Ce qui correspond à environ 0,223 mm. Nous avons maintenant besoin d’un modèle structurel transitoire pour simuler les déflexions au moment de l’impact de notre barre cylindrique sur le sol et après.

Figure 6 : Modèle d’analyse structurelle transitoire et contraintes
Notre modèle suppose que la barre se déplace à une vitesse de 4428 mm/s dans la direction négative Y. C’est la vitesse que la barre atteindrait si elle était lâchée d’un mètre. C’est la vitesse que la barre atteindrait si elle tombait d’un mètre. Nous pouvons calculer cette vitesse en mettant en équation l’énergie potentielle de l’arbre et son énergie cinétique à l’instant de l’impact.
Énergie cinétique :
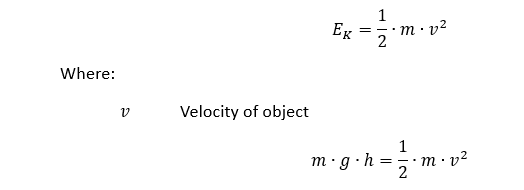
Par conséquent :

Des contraintes sont ajoutées pour maintenir la stature verticale de la géométrie, tandis qu’un support de compression uniquement est ajouté à la base. La durée de l’analyse est définie (nous y reviendrons), ainsi qu’un taux de capture fréquent pour la collecte des résultats.
Les résultats de l’analyse sont compliqués, car lorsque le haut de la barre est dévié vers le bas après l’impact, le bas de la barre peut être légèrement comprimé en raison de la rigidité associée au support de compression uniquement. C’est la différence de déviation entre ces deux surfaces qui décrit la compression globale de la barre.
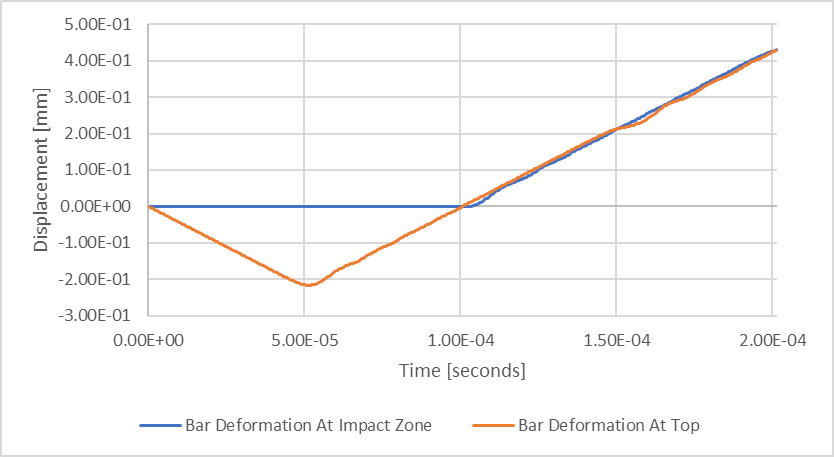
Figure 7 : Résultats de la déflexion structurelle transitoire
La période plate de la ligne bleue, « Bar Deformation at Impact Zone », indique la période pendant laquelle le contact à la base se produit, ou le temps associé à l’impact. Si nous redessinons nos données pour nous concentrer sur cette période, nous pouvons plus facilement faire plusieurs observations.
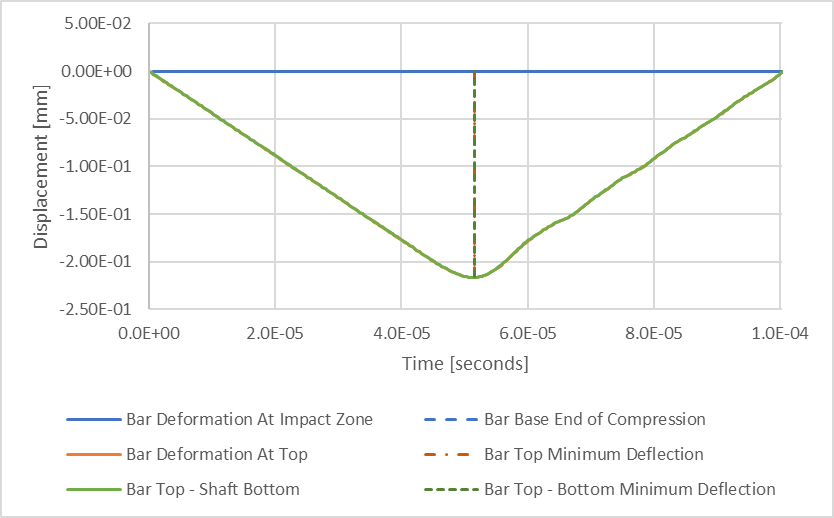
Figure 8 : Résultats de la déformation structurelle transitoire en compression
J’ai ajouté une ligne verte qui représente la différence entre les déformations de la surface supérieure et inférieure de la barre, ce qui donne la compression totale de la barre en fonction du temps. Les deux lignes verticales en pointillés représentent les intervalles de temps associés aux résultats minimaux pour les lignes orange et verte. On peut constater que la compression minimale de la barre se produit en même temps que la compression minimale de la partie supérieure de la barre. Nous pouvons donc estimer que la compression maximale de notre barre est de 0,216 mm, soit un peu moins de 3 % de moins que la déflexion maximale estimée à 0,223 mm.
Il y a cependant plus à explorer et à apprendre de cet exemple et de ses résultats.
Examinons maintenant l’aspect de la mise en place d’une analyse structurelle transitoire, et abordons spécifiquement la période de temps associée à notre événement et déterminons comment nous pouvons estimer cette période pour n’importe quelle géométrie.
Si nous regardons le moment où la ligne bleue est passée d’un déplacement négatif à un déplacement positif (0,00010026 seconde), cela correspond à la période associée à la compression de notre arbre.
Notre arbre peut être considéré comme un ressort qui rebondit. La durée de l’impact reflète ½ de la période de sa fréquence naturelle dans la direction de la compression. Par conséquent, ce qui suit devrait être vrai.

Voyons maintenant si nous pouvons étayer cette théorie et comment nous pouvons estimer la fréquence naturelle de cette géométrie et de toute autre géométrie que nous espérons analyser à l’avenir.
Nous pouvons modifier le support « compression uniquement » appliqué au modèle d’essai ci-dessus, avec une contrainte de direction Y sur ces mêmes surfaces et résoudre directement notre fréquence de vibration longitudinale dans ANSYS.
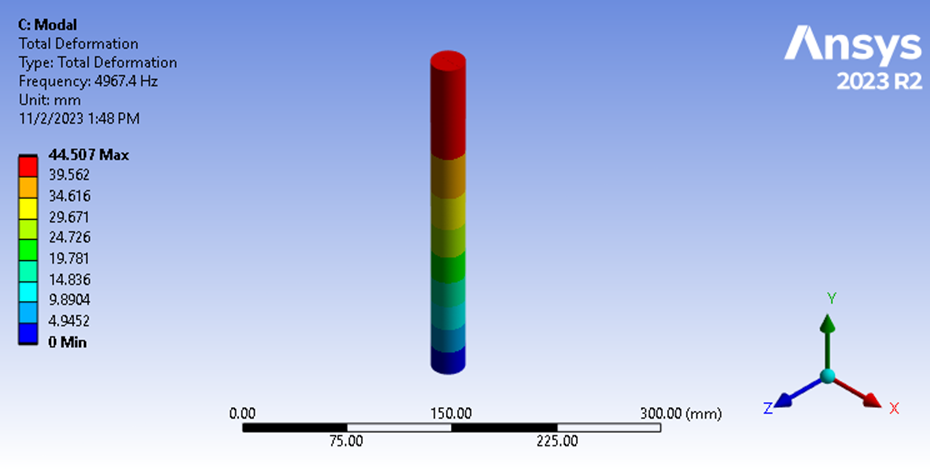
Figure 9 : Fréquence fondamentale de l’analyse modale
Nous voyons ici que la fréquence de vibration longitudinale est de 4967,4 Hz. Cela montre que notre estimation de la fréquence naturelle basée sur nos résultats de déplacement structurel transitoire était précise à 0,4 % près. Cette constatation confirme notre théorie selon laquelle la durée de l’impact est égale à ½ de la période de la fréquence fondamentale pour les objets plus souples qui s’entrechoquent.
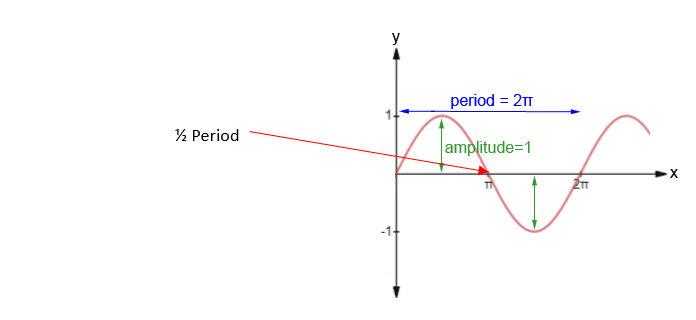
Figure 10 : Période d’impact
Dans notre exemple d’analyse, nous n’avons qu’une seule partie et nous supposons que le support vertical, qui n’est soumis qu’à une compression, représente un autre objet très rigide. Par conséquent, notre arbre est le plus flexible de ces deux partenaires d’impact. Notre analyse structurelle transitoire a été définie pour avoir une durée d’analyse égale à la période de cette fréquence naturelle, et nous nous attendons à ce que l’impact se produise pendant la première ½ de cette période.
Mais comment calculer cette fréquence naturelle si nous effectuons une analyse structurelle transitoire ?
Nous pouvons faire ce que je viens de démontrer, c’est-à-dire effectuer une analyse modale de la géométrie, tout en utilisant des contraintes pour maintenir la posture d’impact et résoudre directement la forme de mode de la compression d’impact. Mais existe-t-il un moyen analytique d’accomplir la même chose ?
Pour explorer cette possibilité, nous devons calculer la fréquence naturelle de notre géométrie dans la direction de l’impact, qui peut être calculée comme suit.

Nous avons déjà exploré la manière dont nous pouvons estimer la rigidité directionnelle, mais examinons maintenant quelques exemples pour mieux comprendre la prise en compte de la masse effective modale.
La masse totale de notre système est de
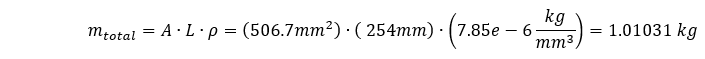
La masse effective de notre système sera inférieure à la masse totale, puisqu’une extrémité de notre géométrie est contrainte. Il peut être difficile d’estimer la quantité de masse qui participera en fonction de la complexité de notre géométrie et des contraintes utilisées pour fixer la géométrie. Dans notre cas, la géométrie est simple et pour les sections transversales extrudées qui sont fixées à une extrémité, la masse effective est souvent calculée comme étant égale à 1/3 de la masse totale du système. Si tel était le cas, notre fréquence fondamentale serait la suivante :
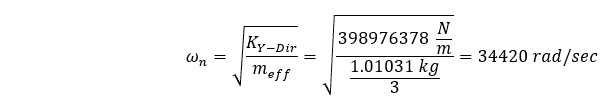
Ce qui peut s’énoncer de manière plus reconnaissable comme suit :
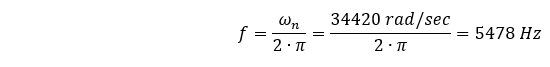
Cette valeur (5478 Hz) est supérieure de plus de 10 % à notre fréquence naturelle (4967,4 Hz) calculée par la méthode des éléments finis… pourquoi ?
La réponse est liée à l’estimation de la masse effective modale. Si nous avons confiance dans le calcul de la rigidité longitudinale (…c’est le cas…), nous pouvons alors modifier la configuration de notre modèle pour vérifier plus facilement le calcul de notre fréquence fondamentale.
Nous fixerons la densité de masse de notre matériau pour notre modèle à zéro, puis nous ajouterons 1,01031 kg de masse à l’extrémité distale de notre géométrie, ce qui devrait produire la fréquence naturelle suivante.
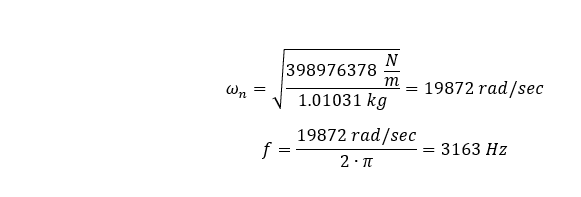
Après avoir effectué l’analyse par éléments finis, nous constatons que la fréquence fondamentale longitudinale est de 3154,6 Hz.
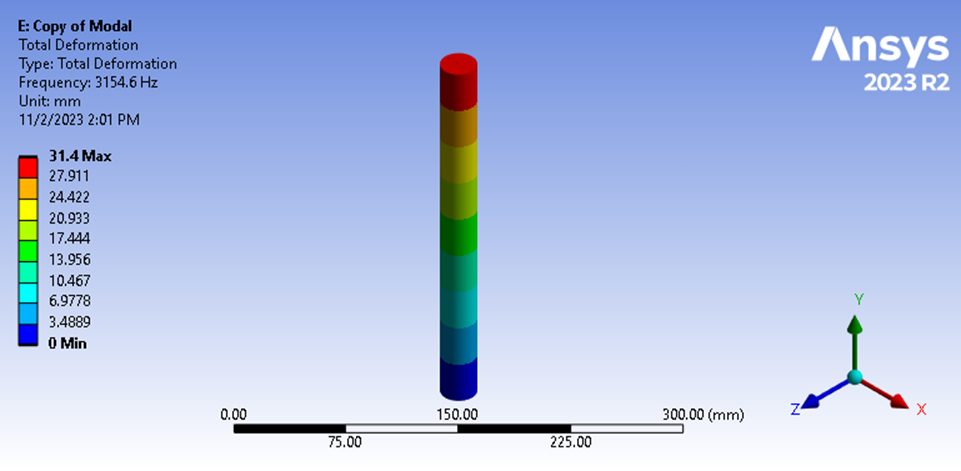
Figure 11 : Analyse modale Fréquence fondamentale
Cela représente une différence de 0,27 % par rapport à notre calcul manuel. Par conséquent, nous avons davantage confiance dans la méthode des éléments finis et nous identifions une faiblesse dans notre estimation de la masse effective utilisée dans notre calcul manuel en utilisant la masse distribuée dans toute notre géométrie.
En réarrangeant notre équation, nous pouvons résoudre cette masse effective en tenant compte de la fréquence naturelle calculée par ANSYS en tenant compte de la masse répartie comme suit :
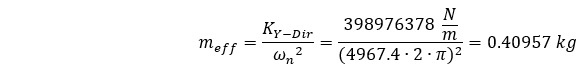
Nous constatons que cette masse effective représente 0,405 de la masse totale du système.
Par conséquent, pour d’autres géométries plus complexes, nous pouvons nous attendre à ce que cette fraction de masse soit unique et difficile à dériver théoriquement et que nous puissions résoudre de manière fiable la fréquence naturelle à l’aide de la méthode des éléments finis.
Maintenant que nous savons comment déterminer la fréquence propre d’une géométrie donnée, nous devons déterminer à quelle fréquence nous devons collecter les résultats de l’analyse pendant notre analyse transitoire.
Pour ce faire, nous devons examiner l’impact de la taille du pas d’analyse sur l’analyse de deux points de vue différents. Le premier point de vue est celui de ce que l’on pourrait attendre en utilisant une caractérisation linéaire par morceaux d’une réponse non linéaire, telle qu’une onde sinusoïdale. L’autre perspective concerne la manière dont les résultats de l’analyse changent en fonction de la modification de la fréquence du taux de capture. Puisque nous considérons un problème d’impact et que nous avons supposé que la période d’impact est associée à la vibration fondamentale de notre composant flexible, il est logique d’explorer la relation entre la taille du pas et son impact sur la précision de la représentation d’une courbe sinusoïdale.
Pour évaluer cette relation, nous comparerons la moyenne pondérée de la magnitude pour la première moitié de la courbe sinusoïdale à la moyenne théorique de cette même portée, qui est égale à :
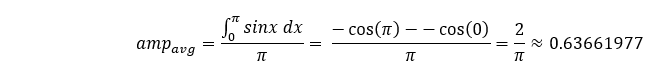
Nous allons maintenant examiner avec quelle précision, en utilisant un nombre différent de pas, nous représentons cette courbe sinusoïdale, puis nous utiliserons la règle du trapèze pour calculer l’aire sous la courbe pour la première moitié, puis nous diviserons cette aire par la période de cet intervalle.
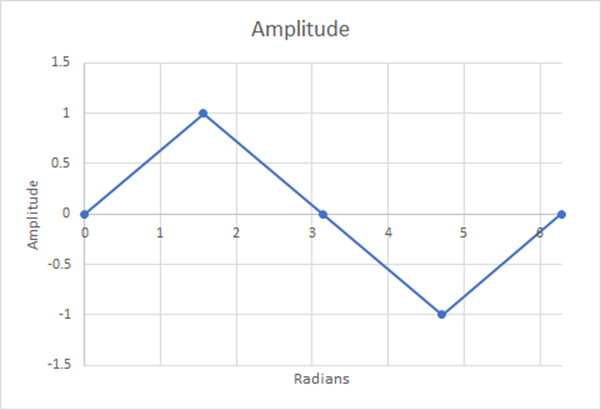
Figure 12 : 4 étapes ; moyenne pondérée estimée = 0,5 ; différence de 21,46 %.
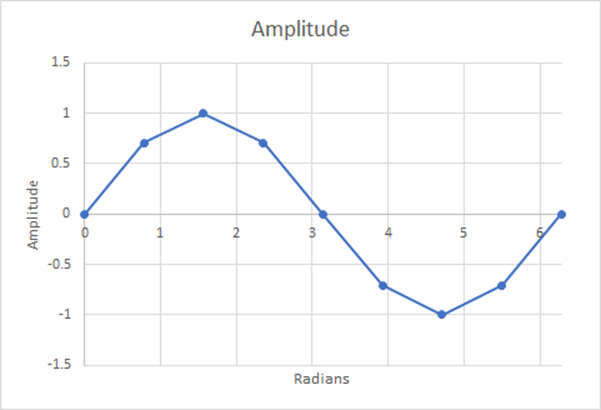
Figure 13 : 8 étapes ; moyenne pondérée estimée = 0,60536 ; différence de 5,19%.
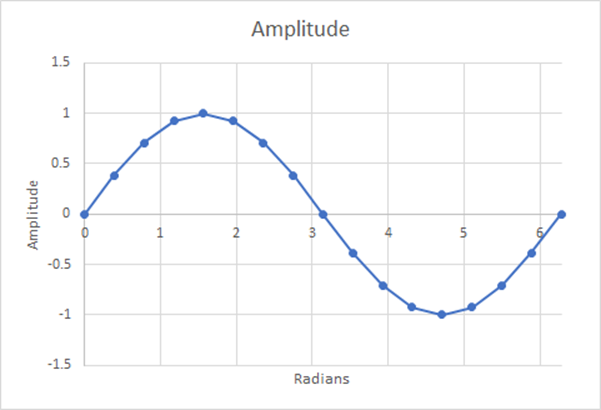
Figure 14 : 16 étapes ; moyenne pondérée estimée=0,6284 ; 1,29% de différence
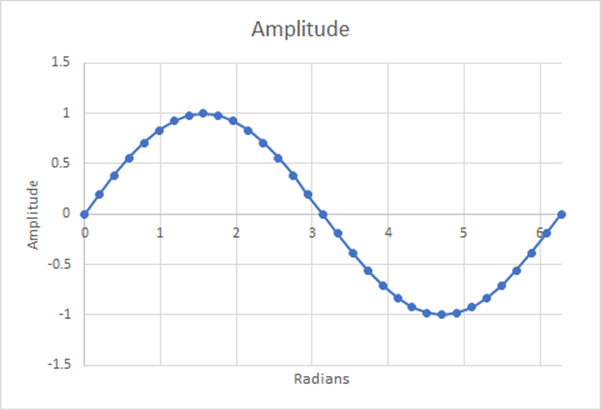
Figure 15 : 32 étapes ; moyenne pondérée estimée=0.6346 ; 0.32% de différence
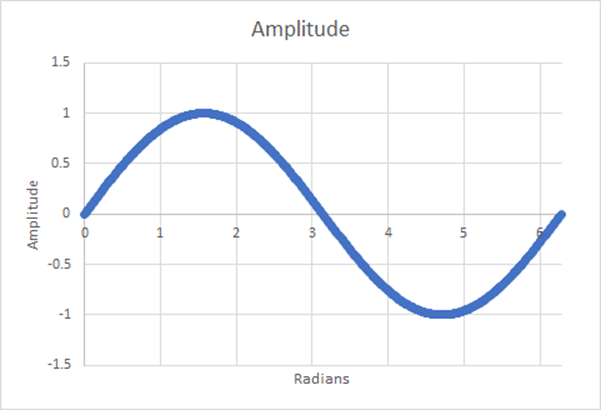
Figure 16 : 512 étapes ; moyenne pondérée estimée = 0,6366 ; 0,001% de différence
En fait, nous ne parvenons jamais à une concordance parfaite avec la valeur théorique, et nous pouvons tracer l’évolution de cette précision au fur et à mesure que le nombre de pas de temps augmente, comme illustré ci-dessous.
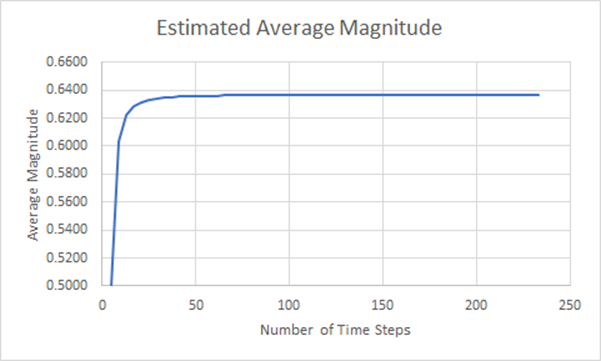
Figure 17 : Diagramme de convergence de la magnitude moyenne estimée
Cet examen nous permet de constater que l’augmentation de la précision est rapide lorsque nous augmentons le nombre d’étapes de notre approximation. Mais cela ne tient pas compte de l’évolution des résultats au fur et à mesure que le nombre de pas de temps augmente.
Pour explorer l’influence sur les résultats de l’analyse, nous allons tracer nos résultats de compression maximale des tiges, en fonction du temps, tout en considérant différents nombres de pas de temps définis dans la solution.
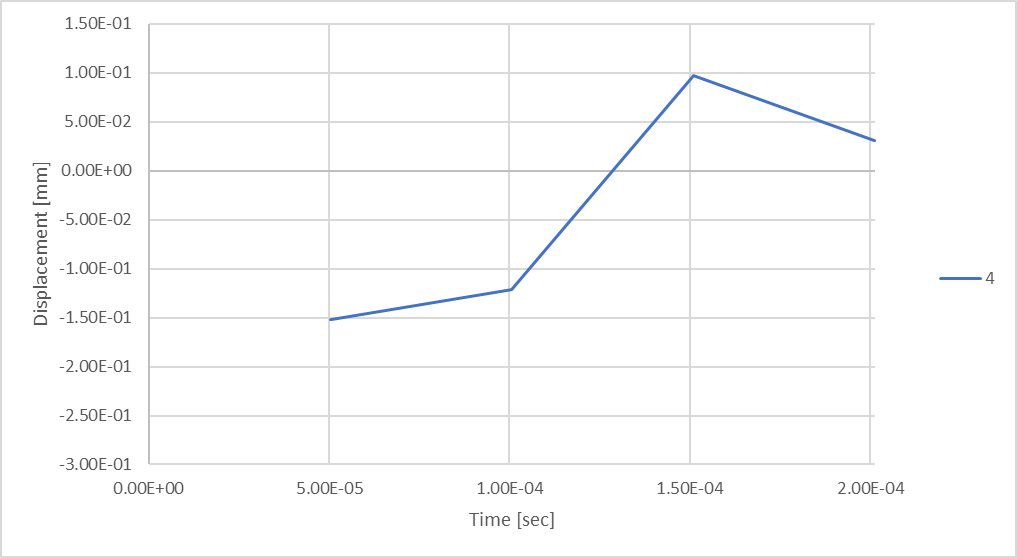
Figure 18 : Déplacement de la tige en considérant 4 pas de temps.
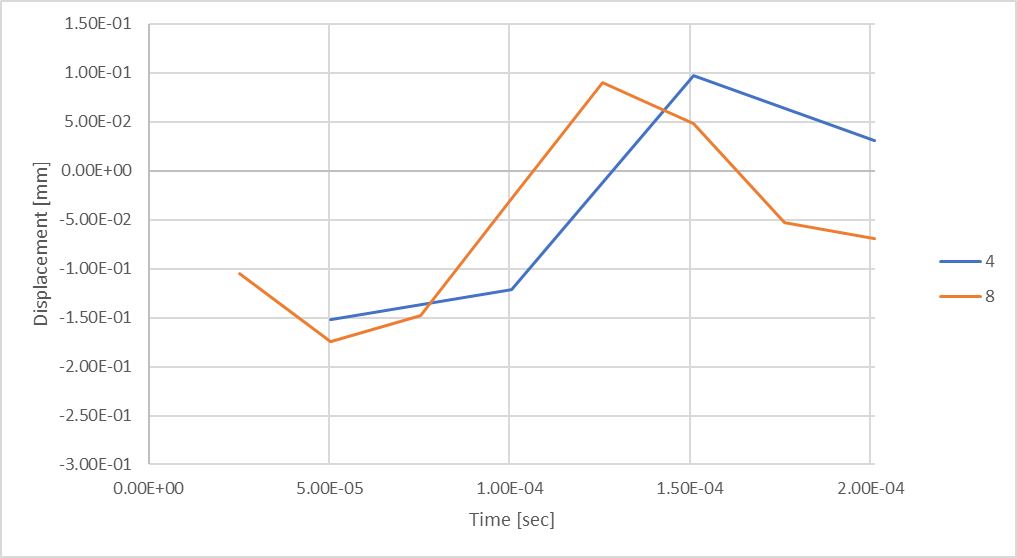
Figure 19 : Déplacement de la tige en considérant 8 pas de temps.
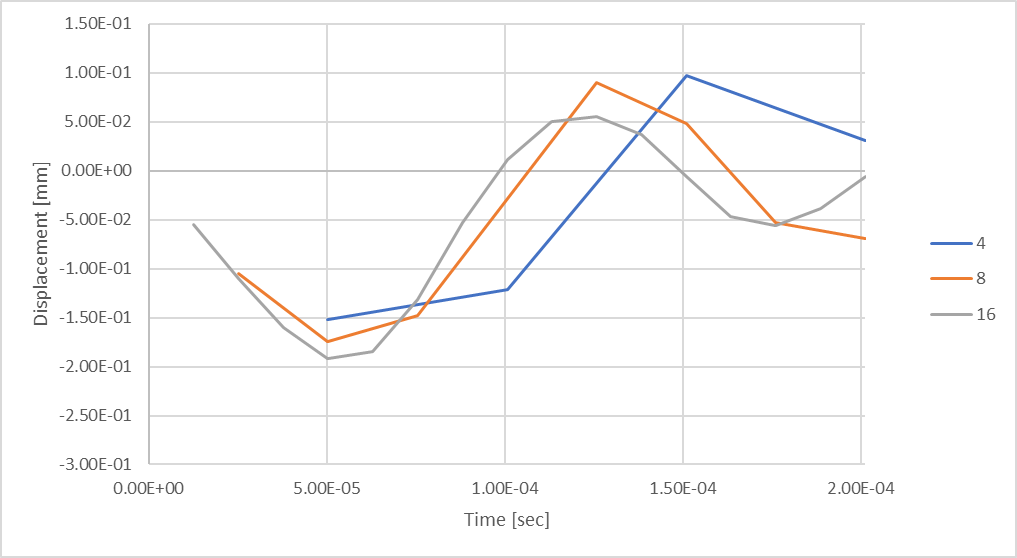
Figure 20 : Avec 16 pas de temps, on observe des déplacements plus importants de la tige en compression.
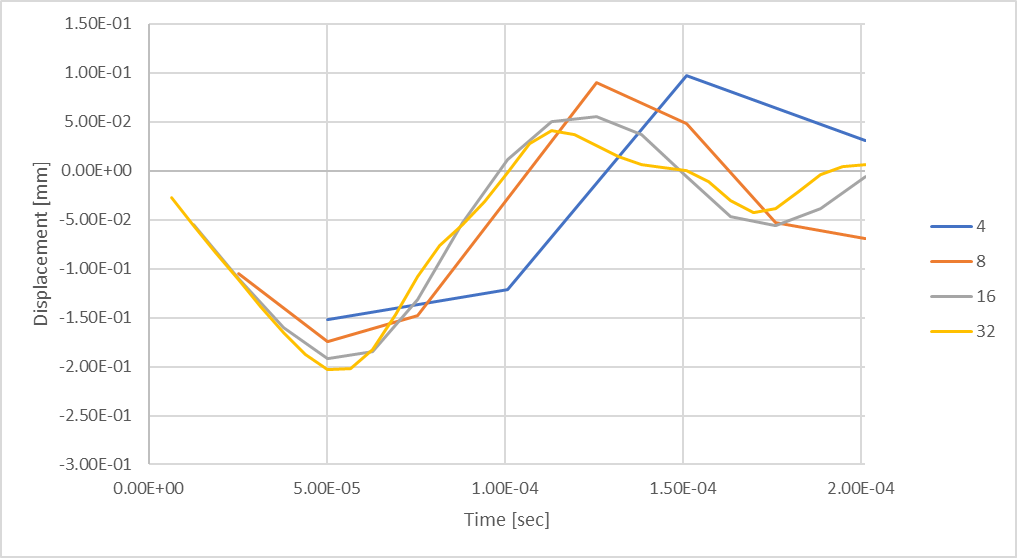
Figure 21 : Déformation maximale transitoire de la tige en utilisant 32 pas de temps.
Sur la base de notre analyse préalable du calcul de l’amplitude sinusoïdale moyenne, nous avons constaté qu’en considérant 32 pas, nous devrions nous attendre à une différence de 0,32 % par rapport aux résultats théoriques. Mais nous pouvons constater que la réponse de notre tige au déplacement en compression est toujours en cours de formation par rapport aux explorations précédentes sur les pas de temps. Que se passe-t-il si nous considérons des pas de temps supplémentaires ?
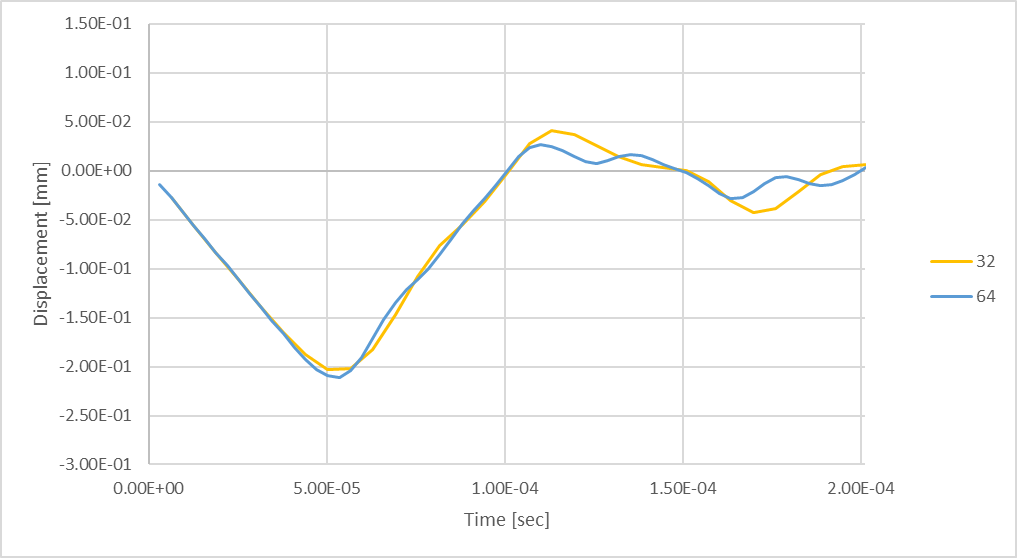
Figure 22 : Déformation maximale transitoire de la tige à l’aide de 64 pas de temps.
L’utilisation de 64 pas de temps produit une déflexion maximale de la tige en compression légèrement plus importante, mais essentiellement similaire, cependant, il y a des signes d’oscillations à plus haute fréquence qui se développent pendant le rebond de la tige.
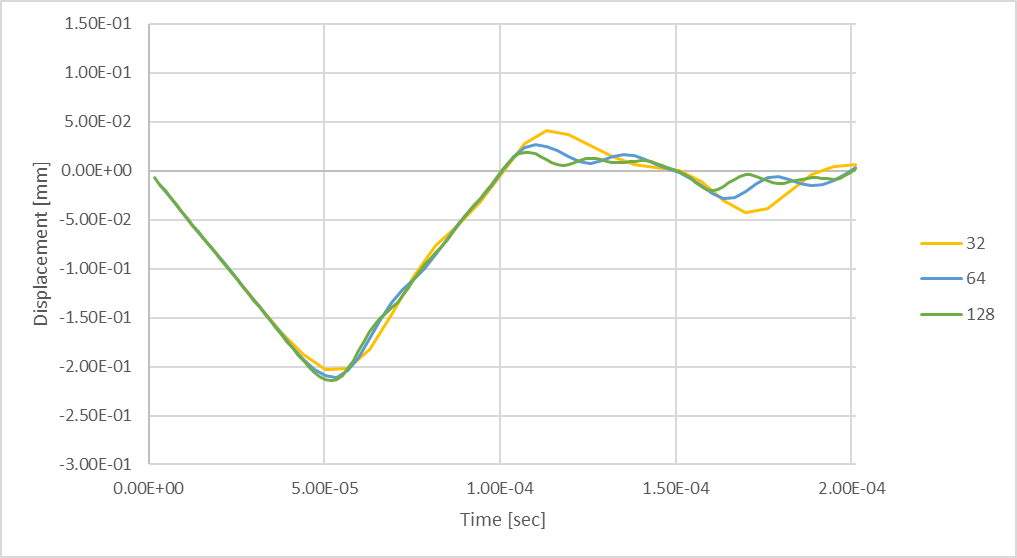
Figure 23 : Déformation maximale transitoire de la tige en utilisant 128 pas de temps.
Si l’on considère 128 pas de temps, la compression maximale de l’arbre est plus importante que si l’on considère un nombre inférieur de pas de temps. La déflexion maximale en compression est supérieure de 6 % à celle obtenue avec 32 pas de temps.
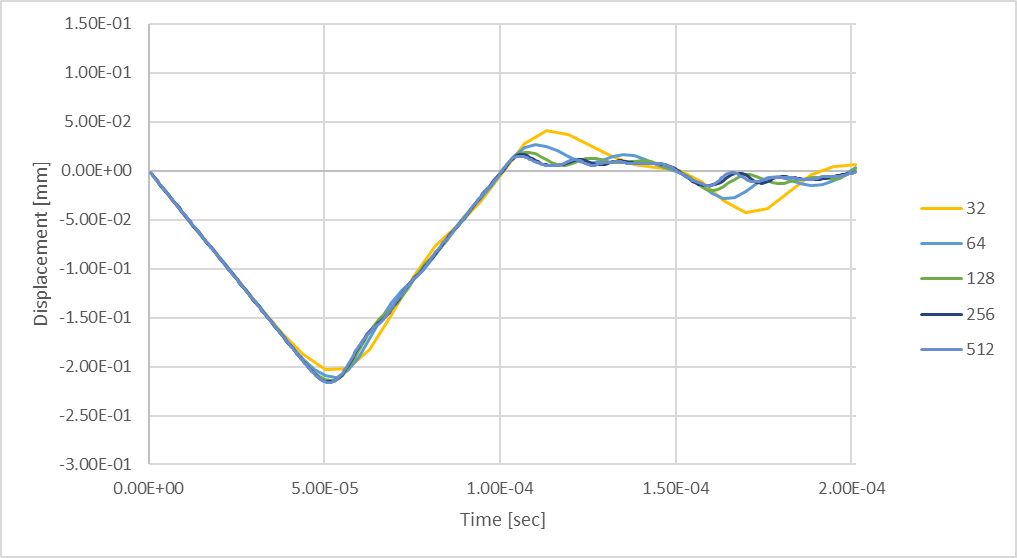
Figure 24 : Déformation maximale transitoire de la tige en utilisant jusqu’à 512 pas de temps.
La comparaison des résultats de l’analyse à 256 pas de temps avec ceux obtenus en considérant 512 pas de temps montre qu’en considérant davantage de pas de temps, il est possible de calculer une plus grande résolution de la réponse dynamique. Le tableau suivant illustre comment on peut s’attendre à ce que les déviations maximales de la tige de compression changent en fonction du nombre de pas de temps pris en compte dans une analyse structurelle transitoire.
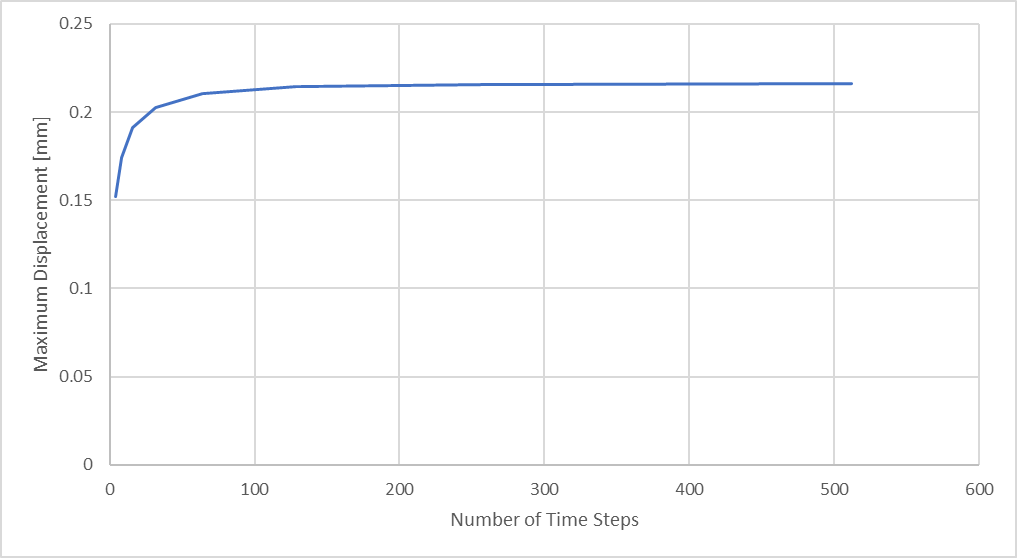
Figure 25 : Déplacement maximal en compression de la tige en fonction du nombre de pas de temps de l’analyse
Finalement, pour une taille de maille donnée, nous atteignons un point de rendement décroissant… où l’effort impliqué par un temps d’analyse prolongé et des fichiers de résultats plus importants n’est pas justifié par un changement significatif dans l’ampleur des résultats.
Sur la base de ces deux considérations, nous pouvons constater qu’en utilisant 32 pas de temps, nous pouvons espérer caractériser une courbe sinusoïdale avec une différence maximale de 0,32 %, mais ne produire que des résultats de déplacement avec une précision de 94 % par rapport à la même analyse utilisant 512 pas de temps, et seulement avec une précision de 91 % par rapport à notre déflexion maximale théorique. La figure ci-dessous montre comment les résultats de la compression maximale de la tige se comparent au maximum théorique estimé.
| Nombre de sous-étapes | Compression maximale | Max théorique | Différence (%) |
| 4 | 0.152139 | 0.222859 | 31.73% |
| 8 | 0.174023 | 0.222859 | 21.91% |
| 16 | 0.191486 | 0.222859 | 14.08% |
| 32 | 0.202746 | 0.222859 | 9.03% |
| 64 | 0.210712 | 0.222859 | 5.45% |
| 128 | 0.214455 | 0.222859 | 3.77% |
| 256 | 0.215752 | 0.222859 | 3.19% |
| 512 | 0.216232 | 0.222859 | 2.97% |
Figure 26 : Déplacement maximal en compression de la tige en fonction des pas de temps de l’analyse
Au fur et à mesure que le nombre de pas de temps augmente, la concordance entre les résultats de l’analyse par éléments finis et la valeur dérivée théoriquement augmente.
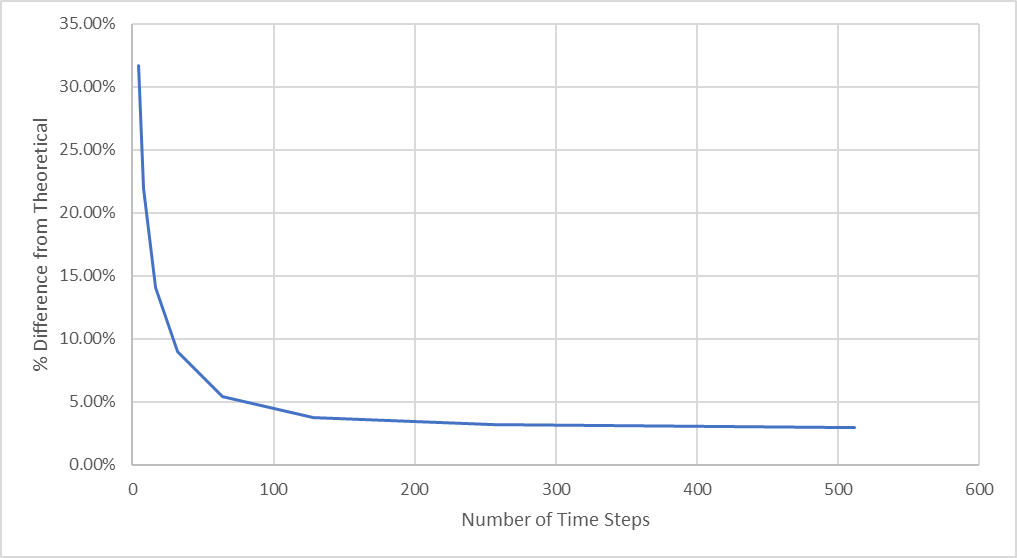
Figure 27 : Différence en pourcentage par rapport à la déflexion maximale théorique
Cette figure montre que la convergence s’améliore considérablement lorsque le nombre de pas de temps est compris entre 64 et 128, mais qu’elle change très peu lorsque le nombre de pas de temps augmente.
Mais qu’est-ce que tout cela signifie en ce qui concerne d’autres résultats, tels que le stress ?
Ci-dessous, je vais tracer la contrainte maximale de von Mises en fonction du temps pour plusieurs scénarios d’analyse.
Figure 28 : Contrainte de von Mises lors de la résolution de 32 pas de temps
Figure 29 : Contrainte de von Mises lors de la résolution de 64 pas de temps
Figure 30 : Contrainte de von Mises lors de la résolution de 128 pas de temps
Figure 31 : Contrainte de von Mises lors de la résolution de 256 pas de temps
Figure 32 : Contrainte de von Mises lors de la résolution de 512 pas de temps
En résumé, voici ce que nous voyons lorsque nous visualisons les contraintes :
| Nombre de sous-étapes | Max Moyenne Contrainte | Contrainte de pointe maximale | Différence en % de la contrainte moyenne |
| 4 | 120.04 | 301.98 | 29.62% |
| 8 | 136.4 | 316.61 | 20.03% |
| 16 | 150.57 | 312.42 | 11.72% |
| 32 | 159.15 | 301.68 | 6.69% |
| 64 | 165.4 | 283.51 | 3.03% |
| 128 | 168.84 | 303.99 | 1.01% |
| 256 | 170.05 | 354.35 | 0.30% |
| 512 | 170.56 | 442.08 | 0.00% |
Figure 33 : Déplacement maximal en compression de la tige en fonction des pas de temps de l’analyse
Nous pouvons constater que les contraintes d’impact maximales deviennent plus importantes à mesure que le nombre de pas de temps augmente, affichant les valeurs les plus élevées au début de l’impact et devenant plus faibles tout au long de l’événement. Les contraintes moyennes dans la tige passent de zéro à un pic au moment de la compression maximale, puis retombent vers zéro après la fin de l’impact. Nous pouvons tracer ces contraintes moyennes maximales ci-dessous.
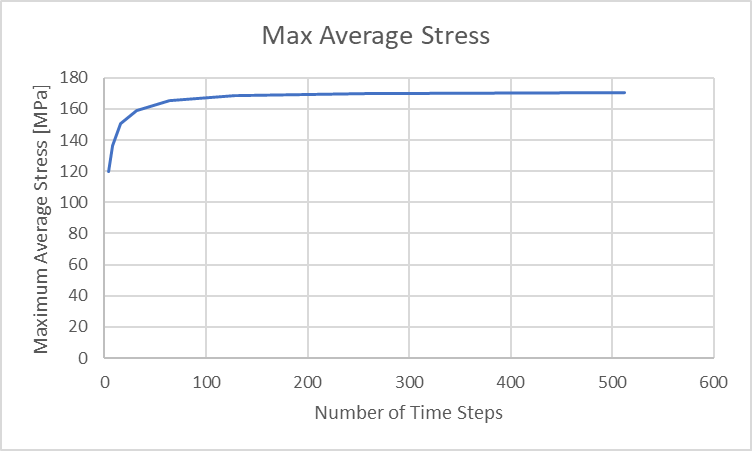
Figure 34 : Déplacement maximal en compression de la tige en fonction des pas de temps de l’analyse
Pour mettre en perspective ces contraintes moyennes maximales, nous pouvons calculer une contrainte moyenne maximale théorique dans notre tige comme suit :
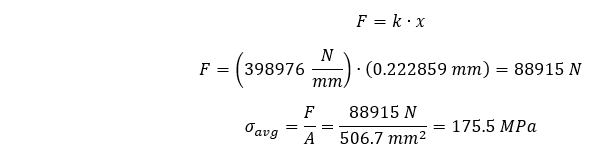
En comparant à nouveau nos contraintes moyennes maximales à notre moyenne maximale calculée théoriquement, nous pouvons résumer la différence en % comme suit :
| Nombre de sous-étapes | Max Moyenne Contrainte | Contrainte moyenne maximale théorique | Différence (%) |
| 4 | 120.04 | 175.5 | 31.60% |
| 8 | 136.4 | 175.5 | 22.28% |
| 16 | 150.57 | 175.5 | 14.21% |
| 32 | 159.15 | 175.5 | 9.32% |
| 64 | 165.4 | 175.5 | 5.75% |
| 128 | 168.84 | 175.5 | 3.79% |
| 256 | 170.05 | 175.5 | 3.11% |
| 512 | 170.56 | 175.5 | 2.81% |
Figure 35 : Déplacement maximal en compression de la tige en fonction des pas de temps de l’analyse
Une fois encore, comme pour les déflexions, nous constatons une amélioration significative de la différence en pourcentage de notre contrainte moyenne maximale par rapport à notre contrainte moyenne maximale calculée théoriquement en considérant entre 64 et 128 pas de temps pour l’événement. Cependant, l’utilisation d’un plus grand nombre de pas de temps n’améliore guère la précision de nos résultats.
Conclusion
Nous avons vérifié que les méthodes énergétiques utilisées pour estimer les déflexions maximales et les contraintes moyennes pour l’événement dynamique, tel que la chute d’un objet élastique sur une surface dure, peuvent produire des résultats raisonnables et que les améliorations les plus significatives en termes de précision se produisent en considérant entre 64 et 128 pas de temps pour un événement égal en période à la fréquence naturelle de notre objet percutant, calculée pour la direction de l’impact. Nous avons également constaté que la meilleure méthode pour approcher cette fréquence naturelle n’est pas le calcul manuel, mais une analyse modale réalisée à l’aide de la méthode des éléments finis, en particulier parce que la quantité de masse effective modale participante n’est pas toujours facile à estimer.
Rejoignez le forum des designers !
Votre expertise est essentielle pour la communauté. Rejoignez-nous et apportez vos connaissances !
Rejoindre le forum maintenantPartagez, apprenez et évoluez avec les meilleurs professionnels du secteur.

