mais dans ce cas, le décalage initial imposé (quel que soit son entité) est un décalage linéaire le long de l'axe du ressort, qui a une direction précise. (si ce n'est pas faux! ! )
c'est là que vous vous trompez.
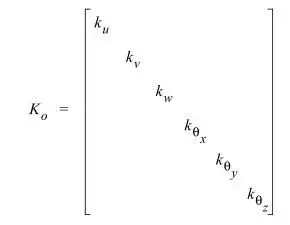
vous dites "un ressort avec une rigidité k", mais k est un nombre ? c'est pas vrai ! est tenseur 3x3 avec sur les rigidités diagonales principales dans les directions x, y et z (et dispersé un peu autour de quelques combinaisons de rigidité torsio, je ne me souviens pas. . )
maintenant, si vous dites "k" signifie que vous faites l'analyse dans une direction, bien sûr le forcinateur doit être dans cette direction.
un faisceau a plutôt des "mortisations" et des "masses" dans toutes les directions, et, si elles sont différentes, chacune d'elles va naître une manière différente de vibrer.
faisons quelque chose. commençons dès le début, excusez-moi si je suis banal, mais je ne veux rien laisser au hasard.
- une source et une masse. le diagramme de bode de ce système est unitaire constant jusqu'à une certaine fréquence, puis il a un asymptote vertical (résonance) puis diminue à quelque chose comme 10 décibels/décennie.
qu'est-ce que ça veut dire ? que si vous soulevez le système avec un sinusoïdal puissant (ce qui est une force pure). la "martellata" de l'onde a transformé quatre plus multi-fréquentiel, capable donc de donner de l'énergie à n'importe quelle façon de vibrer, qui alors commencera son évolution libre), donc, si vous chatouillé avec une force, vous aurez d'abord que le déplacement de la masse est égal à celui de la force, puis il commence à augmenter jusqu'à ce qu'il devienne hypothétiquement infini à la fréquence de résonance, puis augmente encore il est réduit à devenir zéro. que la fréquence de résonance est la fréquence appropriée du système "discret". signifie que si elle est stressée à cette fréquence, les oscillations augmentent indéfiniment, si vous fournissez de l'énergie au système, elle commencera à osciller juste à cette fréquence.
- oui. nous ajoutons un amortisseur. qu'est-ce qui se passe ? déplace un peu la fréquence de résonance, l'ascension devient un maximum local, et, augmentant l'amortissement, au-delà d'une certaine valeur, appelée critique, disparaît elle-même. le diagramme bode est constant jusqu'à ce que la résonance commence à descendre, mais il n'y a plus de résonance. qu'est-ce que ça veut dire ? qu'un système mass-modal, à l'intérieur de la confiture ne peut pas être mis en résonance, il semble évident, mais bode confirme
- maintenant nous ajoutons un autre système masse-molla-smorzator, avec des valeurs différentes, en dessous du précédent. pour corriger des idées, nous disons une masse beaucoup plus petite. qu'est-ce qui se passe ? il y aura d'abord une fréquence à laquelle il commence à osciller la première masse (plus grande), tandis que le petit suit le fort, puis à la main le premier réduit les oscillations et le second augmente, jusqu'à ce qu'ils arrêtent les deux. mais attention, il y a une fréquence intermédiaire dans laquelle les deux masses commencent une oscillation mutuelle. que notre système discret à deux masses n'a pas deux, mais trois propres fréquences, ou des façons de vibrer.
- maintenant nous ajoutons beaucoup d'autres petites entités "massa-molla-smorzatore". nous avons une "trave" élastique qui, à chaque fréquence, répondra d'une manière différente. il y a certaines fréquences où leurs propres façons s'annulent, d'autres dans lesquelles elles se résument. le diagramme de bode aura un ensemble de pics, chacun correspondant à une manière appropriée. sous une force égale à un pic de celui-ci, le faisceau peut subir une contrainte critique.