Taipan95
Guest
Bonjour à tous, je suis un nouvel utilisateur du forum! Je suis étudiant à la polytechnique de Torino, je vais au magistère. Je voulais proposer un exercice sur roues denses avec des doutes attenants sur la transmission des forces/couples: placer le schéma avec les données et illustrer ma procédure.
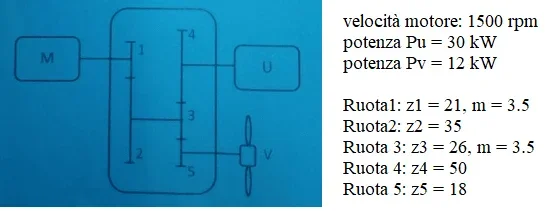Fondamentalement, grâce à un système d'engrenages, une puissance de conduite est transmise à deux utilisateurs différents. les doutes ne concernent qu'une partie de l'exercice, c'est-à-dire celui qui exige d'identifier la roue la plus stressée et de calculer le coefficient de sécurité pour la vérification statique des lewis sur cette roue.
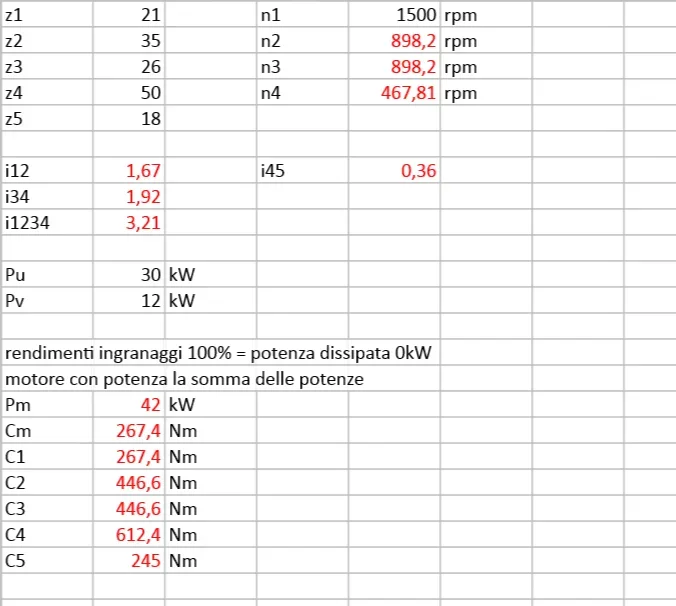
J'ai commencé par calculer le couple d'entrée, en plaçant la puissance d'entrée comme somme de ceux sur les deux sorties: c1 = 267,5 nm.
d'ici c2 = c1*z2/z1 = 445,8 nm, ainsi que oméga2 = r1/r2 * oméga1 = 94,2 rad/s = oméga3 puisqu'ils sont moulés sur le même arbre (idém pour la paire).
poursuivre avec ces formules Je suis arrivé à la conclusion que oméga5 = 136,1 rad/s et oméga4 = 49 rad/s.
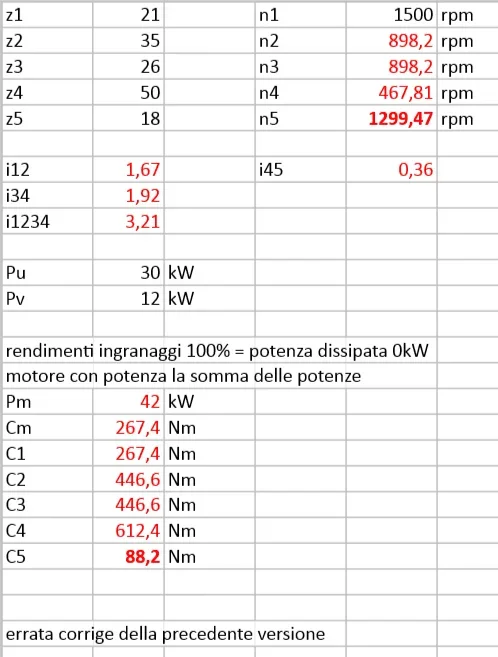
Maintenant, je pose la question: la paire de sortie, par exemple sur la roue 4, devrait être calculée comme pu/omega4 ou comme (pin - pu)/omega4? Je demande cela parce que suivant la première route je trouve deux paires sur roues 4 et 5 paires à 612.2 et 88.2 nm, au lieu de dans le second cas 244,9 et 240.2 nm respectivement.
J'avais ce doute parce que je ne comprends pas pourquoi il n'y a pas d'équilibre des couples, en ce sens que (je crois) les couples sortants en 4 et 5 devraient équilibrer le couple entrant en 3, donc la somme des couples 4 et 5 devrait donner 445,8 nm. en utilisant la "deuxième rue" Je trouve un résultat de 465 nm (quoique incorrecte, mais beaucoup plus similaire à ce que je trouverais en utilisant la première alternative!). dans les deux cas, les deux forces (obtenues en paires / rayons respectifs) seraient 2800 et 6997 n (évidentement inversées... dans le premier cas 2800 serait d'une roue, dans le second cas il serait de l'autre) et donc (2800+6997*r3 me donnerait 445,8 nm confirmant l'équilibre. Ce que je ne comprends pas, c'est si l'équilibre doit avoir lieu pour les couples "purs" ou pour les couples destinés à "force*rage complet".
Je m'excuse à l'avance d'être prolongé, je remercie à l'avance quiconque veut contribuer pour la patience!
Fondamentalement, grâce à un système d'engrenages, une puissance de conduite est transmise à deux utilisateurs différents. les doutes ne concernent qu'une partie de l'exercice, c'est-à-dire celui qui exige d'identifier la roue la plus stressée et de calculer le coefficient de sécurité pour la vérification statique des lewis sur cette roue.J'ai commencé par calculer le couple d'entrée, en plaçant la puissance d'entrée comme somme de ceux sur les deux sorties: c1 = 267,5 nm.
d'ici c2 = c1*z2/z1 = 445,8 nm, ainsi que oméga2 = r1/r2 * oméga1 = 94,2 rad/s = oméga3 puisqu'ils sont moulés sur le même arbre (idém pour la paire).
poursuivre avec ces formules Je suis arrivé à la conclusion que oméga5 = 136,1 rad/s et oméga4 = 49 rad/s.
Maintenant, je pose la question: la paire de sortie, par exemple sur la roue 4, devrait être calculée comme pu/omega4 ou comme (pin - pu)/omega4? Je demande cela parce que suivant la première route je trouve deux paires sur roues 4 et 5 paires à 612.2 et 88.2 nm, au lieu de dans le second cas 244,9 et 240.2 nm respectivement.
J'avais ce doute parce que je ne comprends pas pourquoi il n'y a pas d'équilibre des couples, en ce sens que (je crois) les couples sortants en 4 et 5 devraient équilibrer le couple entrant en 3, donc la somme des couples 4 et 5 devrait donner 445,8 nm. en utilisant la "deuxième rue" Je trouve un résultat de 465 nm (quoique incorrecte, mais beaucoup plus similaire à ce que je trouverais en utilisant la première alternative!). dans les deux cas, les deux forces (obtenues en paires / rayons respectifs) seraient 2800 et 6997 n (évidentement inversées... dans le premier cas 2800 serait d'une roue, dans le second cas il serait de l'autre) et donc (2800+6997*r3 me donnerait 445,8 nm confirmant l'équilibre. Ce que je ne comprends pas, c'est si l'équilibre doit avoir lieu pour les couples "purs" ou pour les couples destinés à "force*rage complet".
Je m'excuse à l'avance d'être prolongé, je remercie à l'avance quiconque veut contribuer pour la patience!
Mais pour éviter que quelqu'un ne soit confondu en lisant ce post, même à l'avenir, j'ai jugé approprié de le dire.