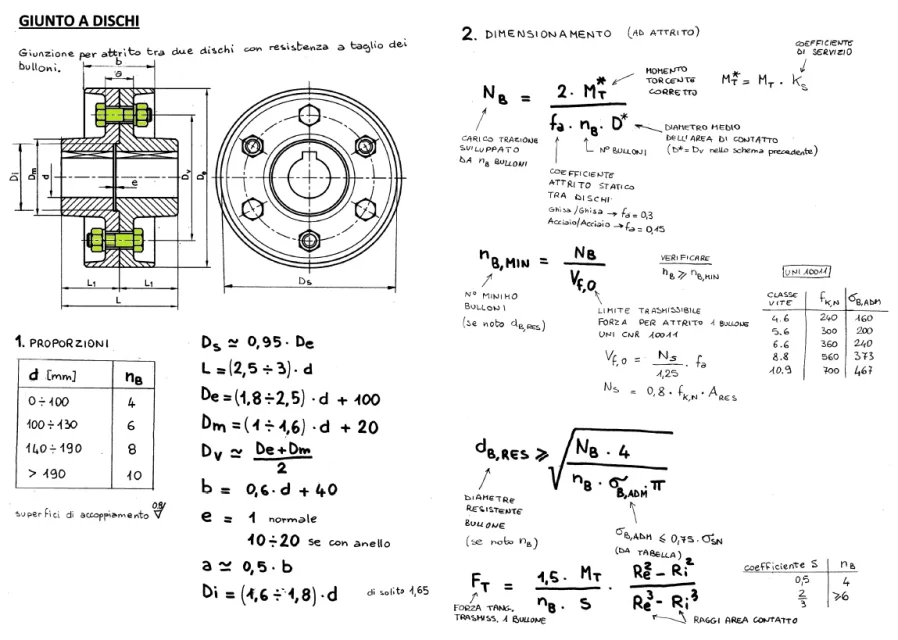
si la puissance, le couple et le régime de rotation sont les trois principales variables qui décrivent une action mécanique qui effectue un travail mécanique.
la paire est une force multipliée par son bras d'action et donc mesurée en [Nm]. le régime de rotation serait la vitesse de l'angle d'oméga mesurée en [rad/s]. la puissance est l'indication du couple dans l'effet de régime, alors:
♪[ P=C•\omega \]où le pouvoir est en [W]comme la vitesse d'angle est plus confortablement indiquée dans [giri/min] vous avez la formule compacte de puissance égale à:
♪[ P=\frac{C•n}{9549,2} \]où le pouvoir est en [kW]après cette prémisse, vous devez considérer que les données que vous avez fournies sont:
- puissance (aucune utilisation)
- Deux.
vous pouvez vous en sortir si vous en avez besoin, comme achèvement
- système de rotation
maintenant vous devez dimensionner l'arbre qui subit comme la seule action décrite dans le texte: le couple ou le moment de torsion, qui est équivalent à une force ronde.
Donc maintenant il doit être dimensionné torsion la section, en supposant un matériau avec ses caractéristiques.
Nous prenons un acier au carbone pour usage général c45. être un acier ductile non fragile a comme caractéristique de donner le rendement.
Je cherche un catalogue en ligne ou un manuel et je vois que grâce à sa charge de rendement rs=400mpa.
l'octaédrique de torsion de tension admissible est:
♪[ \tau_{adm}=0,58•\frac{Rs}{K} \]avec k le coefficient de sécurité qui s'applique normalement à 1,5 pour les applications normales, mais qui peut également être multiplié par deux en cas de chocs forts et de conditions particulières.
une section circulaire avec un diamètre de torsion à partir d'un moment de couple mt génère une tension de couple qui vaut:
♪[ \tau=\frac{Mt}{Wt} \]où wt est le module de torsion de la section à l'étude qui vaut pour une ronde complète:
♪[ Wt=\frac{Jp}{r} \]où jp est le moment d'inertie polaire et r est de demi-diamètre, c'est-à-dire la distance baricentrique maximale.
♪[ Wt=\frac{\pi•d^3}{16} \]maintenant égalant la tension admissible et la vraie est obtenue comme une formule inverse le diamètre de l'arbre
♪[ d≥\sqrt[3]{\frac{16*mt•k}{\pi•0,58•rs}}\]
La théorie la trouve aussi
pour.
Donc, trouvez à ce sujet...30mm d'arbre:
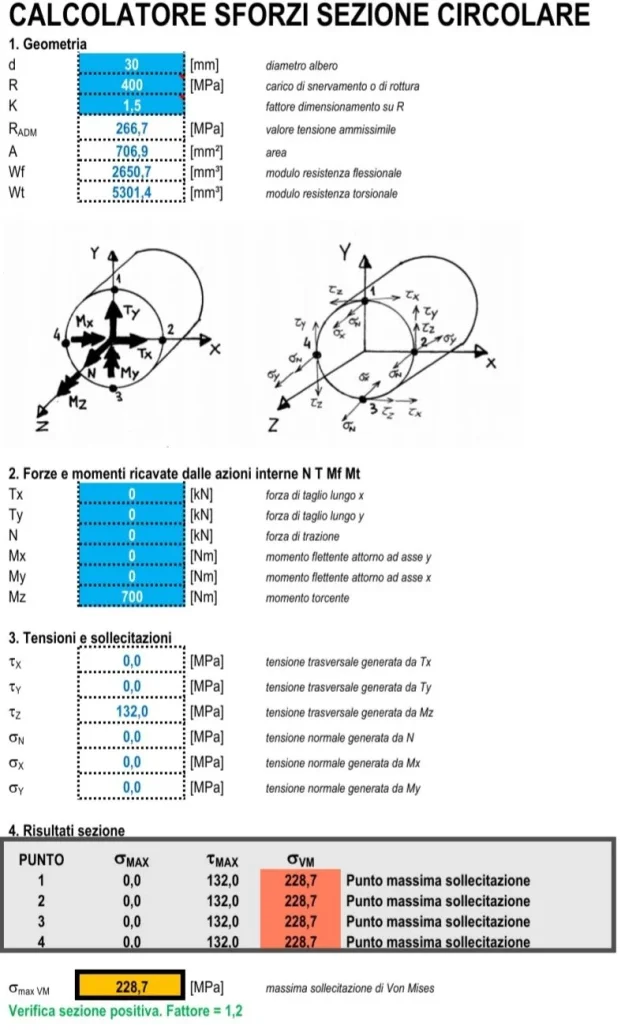
C'est bon ?
Tu comptes et tu me le dis.
Puis on parle du joint...