Explication des moments d’inertie de masse dans SOLIDWORKS

Rejoignez le forum des designers !

Votre expertise est essentielle pour la communauté. Rejoignez-nous et apportez vos connaissances !

Partagez, apprenez et évoluez avec les meilleurs professionnels du secteur.

Nous avons tous fait référence aux propriétés de masse lorsque nous travaillons avec des modèles solides, en particulier lorsque nous prenons des mesures de masse. Certifications SOLIDWORKS! La plupart des informations utiles sont disponibles en un coup d’œil : Densité, Masse, Volume, Surface, etc. Mais comment interpréter le reste des informations contenues dans les propriétés de la masse, en particulier les chiffres en bas de page ? Que nous disent-ils exactement ?

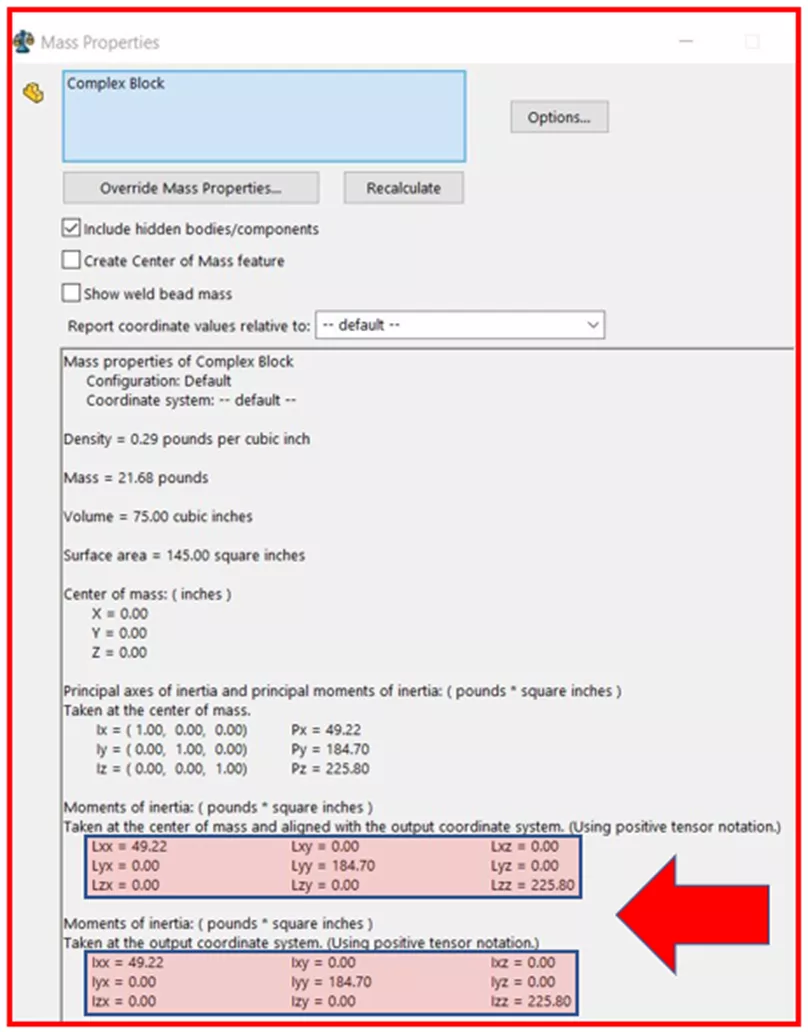
Tout repose sur les moments d’inertie qui dépendent de la masse, de la forme et de l’axe d’un objet. rotation.

Chaque objet possède un centre de masse qui, s’il est suspendu en l’air à partir de ce point, sera parfaitement équilibré. En prenant l’objet symétrique suivant bloc complexe à titre d’exemple, nous pouvons voir les axes principaux passant par son centre de masse.

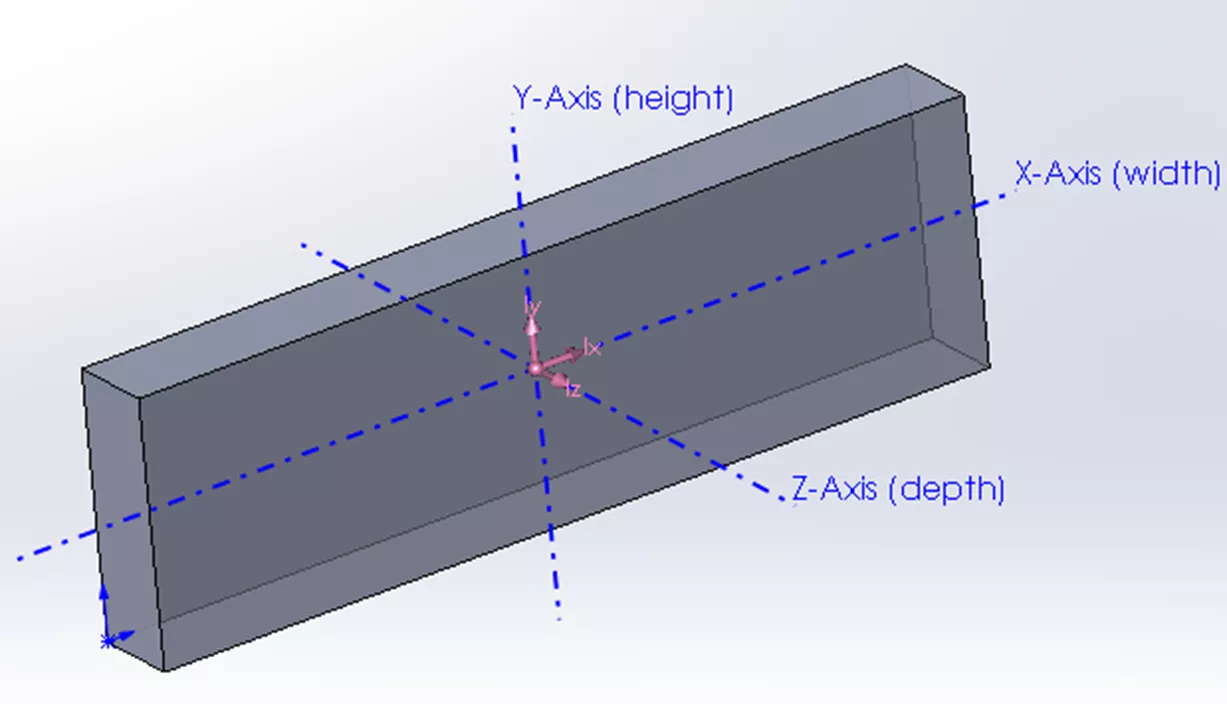
Si le bloc pivote autour de l’un de ces axes, nous verrons les valeurs principales de la masse et du moment d’inertie, qui sont affichées en unités de ML.². Ces valeurs représentent la distribution de la masse autour de chaque axe.

Les groupes de nombres (matrices 3×3) au bas de la fenêtre Propriétés de masse représentent Tenseurs d’inertie.

Sans entrer dans les détails, les éléments diagonaux de ces matrices représentent toujours Moments d’inertie de masse autour des axes primaires d’un système de coordonnées établi. Tout élément non diagonal représente un MOI des produits croisés. Le produit croisé MOI n’est en fait qu’une indication de la symétrie de l’objet. S’il n’est pas nul, on peut s’attendre à un couple ou à une accélération hors axe qui se traduira par une oscillation de l’objet, et non par une rotation pure et simple. Pensez à une roue de voiture équilibrée afin d’éviter toute oscillation.

Examinons un exemple d’objet symétrique par rapport à un seul plan (XY) :

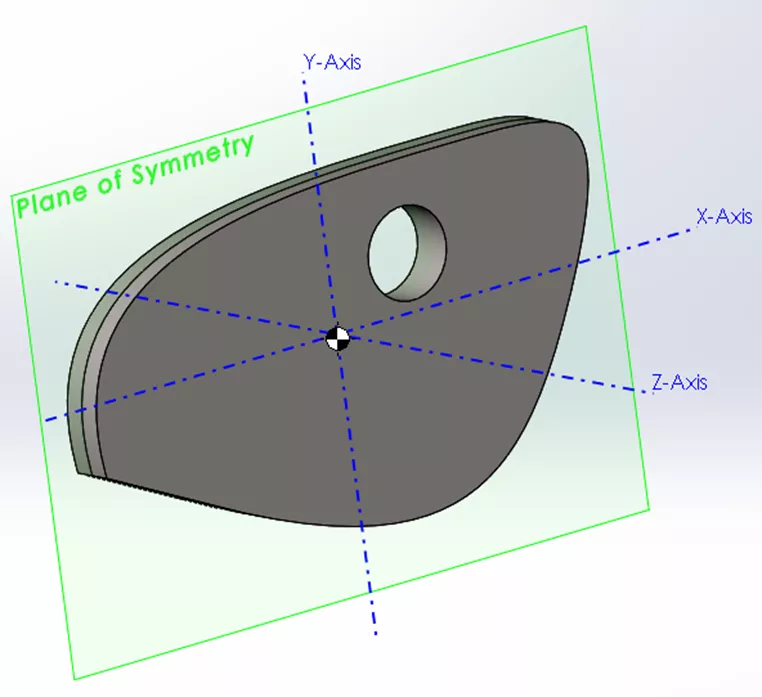
Nous voyons ici des valeurs nulles pour tous les produits croisés contenant l’axe Z (pas d’oscillation dans la direction Z). Cela s’explique par le fait que la masse de l’objet est équilibrée le long de cet axe de part et d’autre du plan de symétrie.

Une façon d’interpréter la notation matricielle est la suivante : si un objet tourne autour de l’axe X, alors Lxx est son inertie « contre » la rotation autour de l’axe X et, simultanément, Lxz est son inertie « contre » la rotation autour de l’axe Z.

Enfin, vous avez probablement remarqué que les propriétés de masse donnent également des valeurs de MOI autour de l’axe X. Système de coordonnées de sortie axes. L’OCS est le cadre de référence par défaut lors de la création d’une pièce, d’un assemblage, etc., et son emplacement dépend donc de la manière dont le modèle est construit.

Dans l’exemple suivant, le bloc a été créé en extrudant vers l’avant à partir de l’origine par défaut (plan avant), de sorte que son OCS est situé dans le coin inférieur arrière gauche. Il est intéressant de noter que l’emplacement du système de coordonnées de sortie peut être facilement modifié même après l’achèvement d’une pièce. Géométrie de référence.

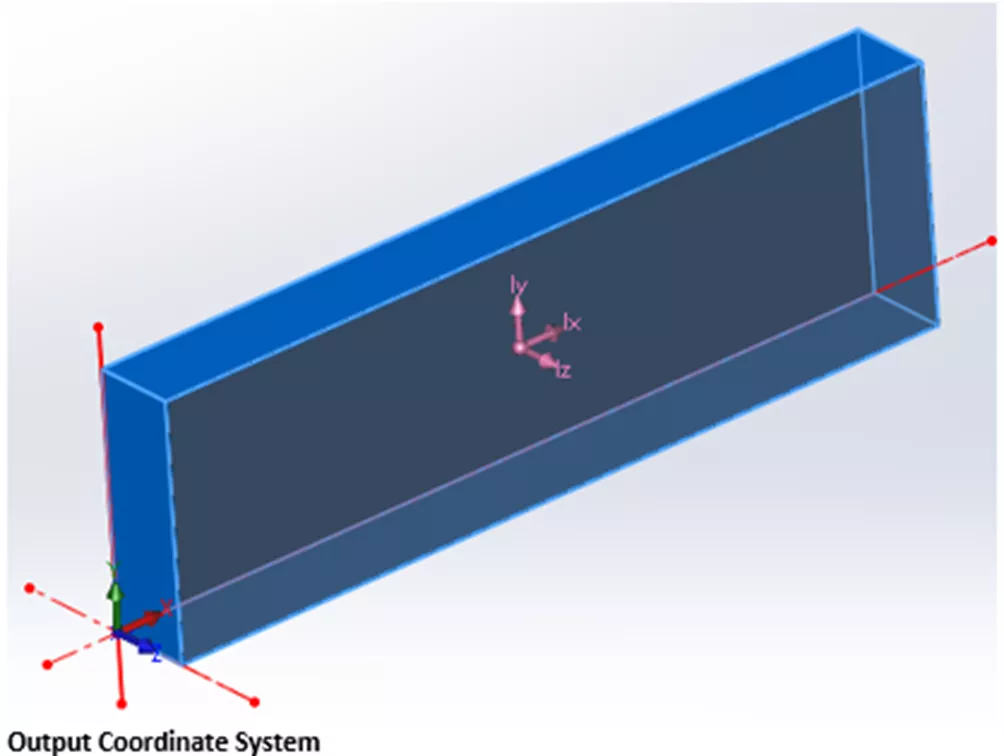
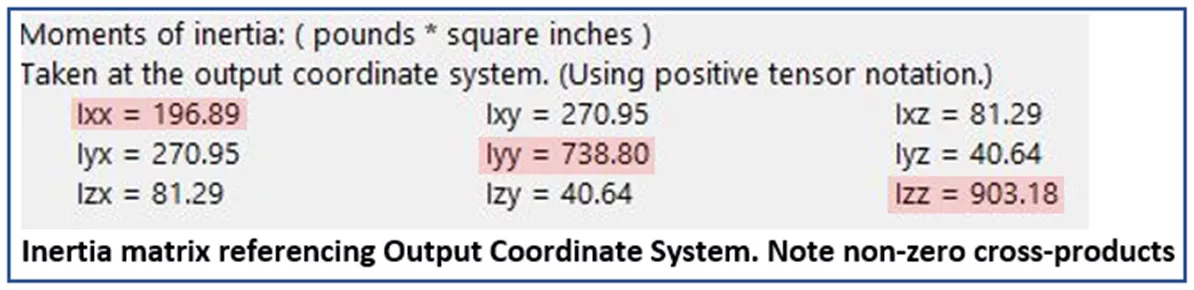
La matrice inférieure des nombres dans Mass-Properties est calculée en se référant au système de coordonnées de sortie de SOLIDWORKS. Système de coordonnées de sortie. Dans ce cas, il est facile d’imaginer notre modèle en rotation autour des axes OCS et, comme on peut s’y attendre, les moments d’inertie sont beaucoup plus importants. Une fois encore, nous voyons le MOI autour de chaque axe exprimé dans les éléments diagonaux, mais cette fois, comme le modèle n’est pas symétrique par rapport à l’un des axes OCS, nous voyons des valeurs non nulles dans tous les produits croisés.

Rejoignez le forum des designers !

Votre expertise est essentielle pour la communauté. Rejoignez-nous et apportez vos connaissances !

Partagez, apprenez et évoluez avec les meilleurs professionnels du secteur.