Le paradoxe des deux condensateurs : la capacité et l’inductance existent-elles ?

Rejoignez le forum des designers !

Votre expertise est essentielle pour la communauté. Rejoignez-nous et apportez vos connaissances !

Partagez, apprenez et évoluez avec les meilleurs professionnels du secteur.

Le paradoxe des deux condensateurs est une expérience de pensée provocante mise en place pour exposer certaines des limites de la modélisation des circuits électriques, et de nombreuses façons différentes de résoudre le paradoxe ont été conçues. J’ajouterai une solution au mélange qui peut être modélisée dans le logiciel COMSOL Multiphysics.^® puis de l’élargir pour poser une question encore plus provocante et y répondre : La capacité et l’inductance existent-elles ? Plongeons dans le vif du sujet !

Le paradoxe des deux condensateurs

Cette expérience de pensée est généralement présentée comme suit : Considérez un dispositif composé de deux condensateurs équivalents, avec une capacité, Cconnectés en parallèle avec un interrupteur ouvert entre eux. Tous les fils et les condensateurs sont constitués de matériaux idéaux, parfaitement exempts de résistance et de pertes. L’un des condensateurs est chargé à un potentiel, V_iLa charge stockée est donc Q = CV_i. Il n’y a pas de différence de potentiel sur l’autre condensateur, qui n’a donc pas de charge stockée. Que se passe-t-il lorsque vous fermez l’interrupteur ?

Schéma du paradoxe des deux condensateurs. Un condensateur a une différence de potentiel entre les plaques. Que se passe-t-il lorsque l’interrupteur est fermé ?

Certaines présentations de cette expérience de pensée jettent un leurre et affirment que la charge du premier condensateur s’écoule dans le second, réduisant la différence de potentiel sur le premier et l’augmentant sur le second jusqu’à ce qu’un état stable soit atteint – à ce moment-là, la différence de potentiel est la même sur les deux condensateurs et la moitié de la différence de potentiel entre les deux plaques est atteinte. V_icar la charge est la même, Qest maintenant répartie sur deux condensateurs équivalents. Cela conduit immédiatement à un paradoxe, car l’énergie contenue dans chaque condensateur est W_C = \frac{1}{2} C \Delta V^2. Si l’énergie initiale est \frac{1}{2} C V_i^2 et l’énergie finale est 2 \frac{1}{2} C\left( V_i/2 \right)^2 = \frac{1}{4} C V_i^2où est passée l’autre moitié de l’énergie ?

Il existe de nombreuses solutions qui font appel à tout ce qui va de la mécanique quantique à la thermodynamique. Ces solutions sont probablement toutes valables d’un point de vue pédagogique. Cependant, nombre d’entre elles font implicitement appel à la réalité en affirmant que les fils et les condensateurs doivent tout simplement avoir une certaine résistance ou une certaine inductance. Mais pourquoi ? Au moins dans le contexte d’une expérience de pensée, il peut être raisonnable de supposer que les matériaux sont parfaitement sans perte, et donc de négliger la résistance. Mais qu’en est-il de l’inductance ? Dans le cadre de cette expérience de pensée, pouvons-nous négliger l’inductance ? Suivons cette question et voyons si elle apporte une réponse intéressante…

Une solution simple au paradoxe

Notre dispositif est composé de deux condensateurs idéaux, sans perte. Mais même un condensateur idéal doit séparer ses charges dans l’espace. En d’autres termes, un condensateur doit avoir une certaine taille. Et si chaque condensateur a une certaine taille, il doit être séparé de l’autre condensateur par une distance non nulle. Si nous redessinons un peu notre schéma, nous constatons que nous avons deux condensateurs et deux demi-boucles de fil sans perte de diamètre fini, le long desquelles un courant variable dans le temps peut circuler. Mais comment appelons-nous une telle structure ? Un inducteur !

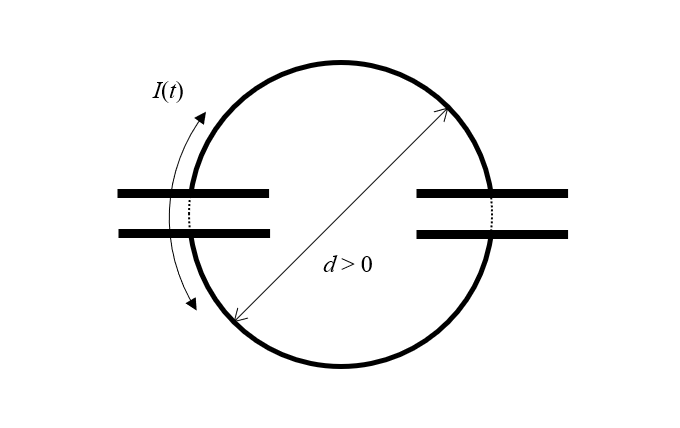
Le paradoxe peut être résolu en réalisant que la structure doit avoir une taille non nulle, le courant circulant autour d’une boucle de surface finie, et qu’elle est donc également un inducteur.

La structure que nous avons dessinée ici doit avoir une taille finie, et donc une inductance, tant qu’elle existe dans notre univers, où l’espace libre a une perméabilité magnétique. Ainsi, la simple conséquence de la présence d’un condensateur dans notre circuit est qu’il doit également y avoir une inductance dans le circuit. En fait, c’est encore mieux : Si nous avons un inducteur, même un inducteur sans perte, tout courant variable dans le temps qui le traverse entraînera un champ électrique entre les spires de l’inducteur, et donc tout inducteur que nous ajoutons à ce circuit agit également comme un condensateur ! Nous pourrions suivre ce raisonnement à l’infini, mais pour nos besoins, il suffit de modifier notre circuit avec un seul inducteur qui a une inductance, L.

Nous disposons maintenant d’un LC Le courant circulera dans les deux sens entre les condensateurs et le long des fils de longueur finie, oscillant à une fréquence donnée par : f=1/\sqrt{2\pi LC}. Il n’y aura jamais de solution en régime permanent et nous ne pourrons donc jamais évaluer l’énergie électrostatique seule. Nous devons également tenir compte de l’énergie due aux charges en mouvement, c’est-à-dire au flux de courant, Iet celle-ci est donnée par : W_L = \frac{1}{2} L I^2. La somme de cette énergie électrique et magnétique (\frac{1}{2} L I^2 + \frac{1}{2} C V^2) ne changera pas avec le temps.

Vérification dans le logiciel COMSOL Multiphysics^® Logiciel

Il est facile de construire un modèle qui vérifie cette situation à l’aide de COMSOL Multiphysics^® et le module RF. Pour ce faire, nous utiliserons le Ondes électromagnétiques, transitoires avec l’interface Électrostatique pour calculer les conditions initiales. Nous modéliserons une petite région de vide parfait avec les condensateurs et les fils à l’intérieur. Les plaques du condensateur, les fils et l’espace autour de notre volume sont tous traités comme des conducteurs électriques parfaits, ce qui signifie que les champs électromagnétiques ne pénètrent à travers aucune limite. Vous trouverez un guide pour la mise en place de ces modèles de décharge capacitive dans notre article du Centre d’apprentissage : « Modélisation de la décharge capacitive ».

La résolution de ce modèle dans le domaine temporel et l’évaluation de l’énergie électrique et magnétique totale montrent le comportement oscillatoire attendu. Il est également possible de diviser le domaine de modélisation en différentes régions pour évaluer l’énergie totale dans les régions autour des deux condensateurs ainsi que dans l’espace environnant. Ce graphique montre comment l’énergie oscille dans l’espace et dans le temps.

Animation montrant les courants à la surface des plaques et des fils du condensateur ainsi que le champ magnétique dans l’espace intermédiaire.

L’énergie électrique et l’énergie magnétique totales oscillent dans le temps ; la somme ne change pas dans ce dispositif sans perte.

Le total de l’énergie électrique et magnétique dans différents domaines montre que l’énergie oscille dans le temps et l’espace.

Nous pouvons observer que ces tracés ne sont pas purement sinusoïdaux dans le temps, et nous devrions nous demander pourquoi. D’où vient ce contenu à haute fréquence, c’est-à-dire les ondulations de l’énergie dans le temps ? Il provient de la structure. Il est évident que les deux plaques ont une capacité bien définie, mais il y a aussi une séparation des charges due aux fils, et toute cette structure se trouve dans une cavité cylindrique qui a une fréquence de résonance. Toutes ces différentes parties du dispositif contribuent d’une manière ou d’une autre au comportement électromagnétique. Chaque contribution peut être très faible, mais elle existe toujours lorsque nous considérons une structure de taille finie.

Poser plus de questions : La capacité et l’inductance existent-elles ?

Il est maintenant temps de poser une question plus provocante au sujet de ce dispositif électromagnétique (ou de tout autre) : A-t-il une capacité ou une inductance ? Nous avons clairement vu que ce dispositif particulier possède les deux. Mais que se passerait-il si nous le modifiions en ajoutant un matériau diélectrique très résistant entre les plaques du condensateur ? La capacité serait alors beaucoup plus grande, mais l’inductance resterait inchangée. Et si nous augmentons considérablement la capacité, pouvons-nous dire que l’inductance n’a pas d’importance ?

En bref : Non, il ne faut jamais penser qu’un dispositif électrodynamique est purement capacitif ou purement inductif. Dans un dispositif électrodynamique, il y aura toujours de l’énergie électrique due à la séparation spatiale des charges et de l’énergie magnétique due au mouvement des charges. Bien que nous puissions parfois construire des situations hypothétiques dans lesquelles l’une ou l’autre peut être ignorée, nous devons toujours nous rappeler que nous procédons à une simplification mentale.

En outre, tous les matériaux réels ont également une certaine résistance finie, de sorte que, pour être plus réaliste, nous devrions parler de tout comme ayant une impédance – et c’est là que nous nous mettons parfois dans une situation encore plus délicate. Lorsqu’il s’agit d’un modèle dans le domaine des fréquences, il existe une expression très familière pour l’impédance d’un appareil électrique :

Z = R + j\oméga L -j\frac{1}{\oméga C}

La résistance, Rdans cette expression est une mesure de la façon dont l’énergie cinétique des charges en mouvement, c’est-à-dire le courant, est convertie en énergie thermique.

Cette équation est immédiatement reconnaissable comme se rapportant à un oscillateur harmonique amorti à un seul degré de liberté, qui est l’un des problèmes les plus étudiés en ingénierie et en physique. Nous savons que nous pouvons calculer à partir de cette expression la fréquence de résonance et le facteur de qualité d’un tel oscillateur, et nous savons que les appareils réels ont une résonance et un facteur de qualité fondamentaux. Nous sommes donc tentés d’assimiler les deux et d’essayer de réduire un dispositif électrique réel, de taille finie, à une résistance, une capacité et une inductance uniques. Il s’agit d’une erreur conceptuelle qui n’est jamais valable, car l’expression ci-dessus pour l’impédance ne s’applique qu’à un dispositif de taille infinitésimale.

Tout dispositif réel a une taille finie et, lorsqu’il fonctionne à la résonance, l’énergie électrique et magnétique varie dans l’espace et le temps, comme nous l’avons vu sur les graphiques ci-dessus. Par conséquent, un modèle de circuit équivalent nécessite au moins trois nœuds au moins trois nœuds, mais parfois beaucoup plus. Si nous revenons à notre modèle physique des deux condensateurs et que nous supposons que la plaque de chaque condensateur est représentée par un nœud dans le circuit électrique, nous pouvons voir que le modèle de circuit équivalent devrait être au moins aussi compliqué que le circuit illustré ci-dessous, avec quatre nœuds. Notez qu’une petite capacité a été ajoutée en parallèle à l’inductance des fils puisqu’il y a également une séparation de charge le long des fils.

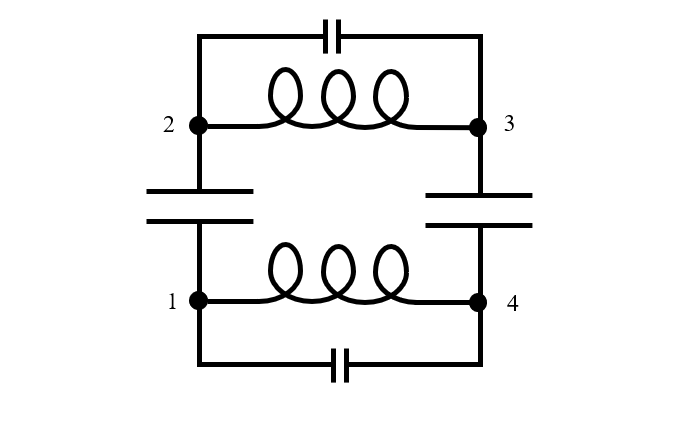
Modèle de circuit équivalent de deux condensateurs sans perte de taille finie connectés en série.

Cet exemple montre que la construction d’un modèle de circuit équivalent valable à proximité de la résonance peut rapidement devenir très complexe et nécessiter des connaissances physiques, une bonne dose d’expérience avec des dispositifs similaires et une modélisation numérique.

Pour en revenir à la question initiale, on pourrait dire que la capacité, l’inductance et même la résistance sont des concepts qui n’existent pas seuls, mais uniquement en combinaison les uns avec les autres. Bien que nous puissions parfois réduire l’impédance d’un dispositif en fonction de la fréquence à une simple résistance, capacité et/ou inductance, de telles simplifications ne sont valables qu’à des fréquences inférieures à la résonance du dispositif. Garder cela à l’esprit nous permet d’éviter toutes sortes d’écueils, allant de l’amusant paradoxe des deux condensateurs à des problèmes réels beaucoup plus complexes et frustrants.

Remarques finales

Nous avons utilisé ici une expérience de pensée classique pour comprendre pourquoi l’impédance d’un dispositif électromagnétique fonctionnant près de la résonance ne peut pas être décomposée en une résistance, une capacité et une inductance équivalentes. Les expériences de pensée telles que le paradoxe des deux condensateurs sont précieuses pour élargir notre compréhension de l’électromagnétisme et interpréter les résultats de nos modèles informatiques.

Pour en savoir plus

Vous souhaitez savoir comment la modélisation et la simulation peuvent être utilisées pour résoudre d’autres casse-tête ? Consultez d’autres exemples sur le blog COMSOL :

Rejoignez le forum des designers !

Votre expertise est essentielle pour la communauté. Rejoignez-nous et apportez vos connaissances !

Partagez, apprenez et évoluez avec les meilleurs professionnels du secteur.