Rejoignez le forum des designers !
Votre expertise est essentielle pour la communauté. Rejoignez-nous et apportez vos connaissances !
Rejoindre le forum maintenantPartagez, apprenez et évoluez avec les meilleurs professionnels du secteur.
Les techniques disponibles en tant que pilotes d'adaptateurs dans Process Composer sont excellentes. Ils sont le résultat de recherches approfondies en méthodes numériques. Les techniques les plus importantes sont le DOE, l'optimisation, les approximations et Six-Sigma. Nous avons discuté du DOE en détail dans les blogs précédents. Dans ce blog, nous approfondissons l'optimisation. N'oublions pas que nous sommes en processus composer, l'optimisation est donc paramétrique principalement pilotée par des paramètres géométriques ou physiques.
La définition classique de l'optimisation
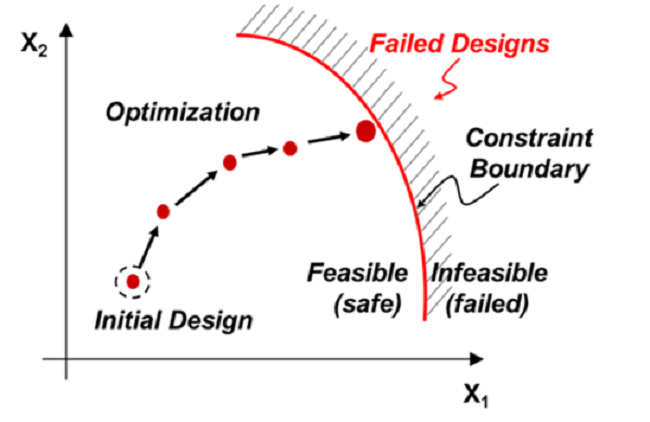
Vous avez une balle quelque part dans le terrain clôturé. Vous avez un point de départ. Vous devez trouver le ballon en parcourant la distance minimale sans franchir la clôture. Vous disposez de capteurs pour vous assister. La balle est la fonction Objectif. Les clôtures sont des contraintes. Les capteurs sont les techniques d'optimisation utilisées.

La différence entre la conception d'expériences et l'optimisation
La différence entre les deux est la même que la différence entre « meilleur » et « meilleur ». Le plan d’expériences est une méthode permettant de sélectionner de manière efficace le point de conception le plus approprié à partir d’un ensemble de points existants. Cet ensemble peut être défini soit par l'utilisateur, soit par le DOE lui-même. Les techniques d'optimisation commencent par un seul point de conception initial et naviguent de manière itérative dans l'espace de conception pour arriver au point de conception optimal ou optimal. Selon le problème, le DOE peut être un précurseur de l'optimisation.
Types de techniques d'optimisation
Il existe différentes méthodes pour les catégoriser en fonction de la façon dont la fonction objectif est définie et du type d'espace de conception approprié.
Techniques contraintes : Ils utilisent des fonctions distinctes pour fonctionner, une pour l'objectif et l'autre pour les contraintes. Nous avons tous vu de telles techniques à un moment ou à un autre lors de cours d'ingénierie. Ce sont les plus courants.
Réduire/Maximiser F(x) dans x1>x>x2
Sous réserve de : h(x)>a1 ; g(x)>a2; f(x)=0 etc.
Techniques sans contraintes : Ils utilisent une seule fonction pour l'objectif et les contraintes. L'utilisateur définit toujours des contraintes distinctes de l'objectif, mais en interne, le problème contraint est converti en un problème sans contrainte.
En fonction de l'application à différents types d'espace de conception, les méthodes d'optimisation peuvent être classées basées sur le gradient, directes ou exploratoires. Les abréviations affichées dans les images ci-dessous sont les noms des méthodes dans les catégories respectives.
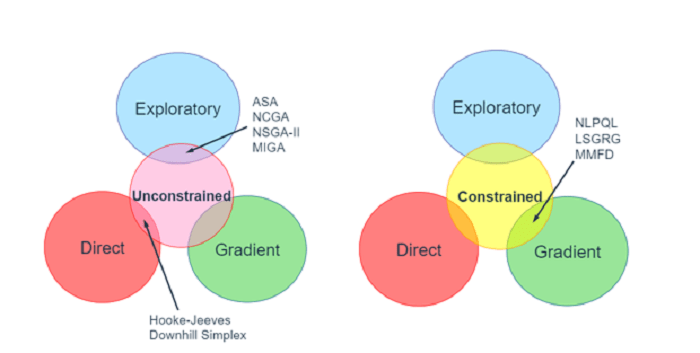
Méthodes de dégradé : Ce sont les plus anciens et ont été bien testés dans l’industrie. Ils fonctionnent selon le principe d'énergie minimale ou de stabilité maximale. Vous lâchez doucement une balle dans une vallée et elle glissera le long du chemin de la pente la plus raide jusqu'à ce qu'elle atteigne le point le plus bas de son voisinage. Ces méthodes fonctionnent dans un espace de conception continu qui a une continuité C0 et C1. Ils sont susceptibles de rester bloqués dans les minimums locaux, le point initial doit donc être soigneusement choisi.

Méthodes directes : Un algorithme de recherche directe commence par un point de base. Il recherche un ensemble de points autour de lui en recherchant celui où la valeur de la fonction objectif est inférieure à celle actuelle. L'algorithme saute à ce point en tant que nouveau point de base et recherche un nouvel ensemble de points autour de lui. On peut comprendre qu’une telle méthode est efficace sur le plan informatique car aucun calcul de gradient n’est requis. Il est plus polyvalent car la continuité C0 et C1 n'est pas requise. Les plus courants sont Hooke's-Jeeves et Downhill Simplex.
La méthode Hooke's Jeeves garde une trace de sa direction de déplacement. Il ne change pas de direction à chaque pas si un point inférieur est disponible dans le sens de la marche.

Méthodes exploratoires: Ces méthodes sont basées sur des techniques de croisement ou de mutation entre un ensemble de données de points appelés parents pour générer un autre ensemble de données de points appelés enfants. Le nouvel ensemble de données évolue à chaque mutation et se rapproche de la solution optimale. Il s'agit d'un schéma haute fidélité qui fonctionne avec toutes sortes de fonctions objectives : discontinues, non différenciables, stochastiques, de type entier mixte et hautement non linéaires avec de multiples pics et vallées, comme indiqué ci-dessous. Cependant, il s’agit du schéma d’optimisation le plus coûteux en termes de dépenses de calcul. Les méthodes les plus courantes sont l’algorithme génétique, l’essaim de particules et le recuit simulé adaptatif.
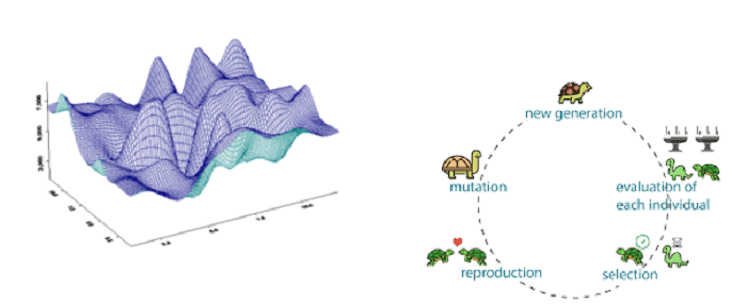
Méthodes basées sur des pointeurs: Il s'agit d'une approche mixte au cas où l'utilisateur n'aurait aucune idée du type de technique qui serait le plus approprié pour résoudre le problème avec une précision raisonnable. L'approche du pointeur peut être utile lorsque l'utilisateur rencontre un type d'espace de conception inconnu et difficile à visualiser. La méthode du pointeur peut utiliser jusqu'à trois schémas d'optimisation, de préférence un de chaque panier : gradient, direct et exploratoire. Au fur et à mesure de l'optimisation, l'algorithme suit l'efficacité de chaque méthode et utilise celle la plus appropriée pour le problème donné.
Rejoignez le forum des designers !
Votre expertise est essentielle pour la communauté. Rejoignez-nous et apportez vos connaissances !
Rejoindre le forum maintenantPartagez, apprenez et évoluez avec les meilleurs professionnels du secteur.

