デザイナーのためのフォーラムに参加しよう
あなたの専門知識はコミュニティにとって不可欠です。私たちに参加して、あなたの知識を提供してください。
今すぐフォーラムに参加する業界最高のプロフェッショナルと分かち合い、学び、成長する.
プロセスコンポーザーのアダプターのドライバーとして利用できるテクニックは素晴らしいです。 これらは、数値手法における徹底的な研究の結果です。 最も著名な技術は、DOE、最適化、近似、シックスシグマです。 DOE については、以前のブログで詳しく説明しました。 このブログでは、最適化について詳しく説明します。 私たちはコンポーザーをプロセス中であるため、最適化は主に幾何学的パラメーターまたは物理パラメーターによってパラメトリックに行われることを忘れないでください。
古典的な最適化の定義
フェンスで囲まれたフィールドのどこかにボールがあります。 あなたには出発点があります。 フェンスを越えずに最小限の距離を移動してボールを見つける必要があります。 支援用のセンサーがあります。 ボールは目的関数です。 フェンスは制約です。 センサーは最適化技術として使用されます。

実験計画法と最適化の違い
両者の違いは、「より優れたもの」と「最高のもの」の違いと同じです。 実験計画法は、既存の点の集合から効率的な方法で最も適切な設計点を選択する方法です。 このセットは、ユーザーまたは DOE 自体によって定義できます。 最適化手法は、単一の初期設計点から始まり、設計空間内を繰り返しナビゲートして、最適または最良の設計点に到達します。 問題によっては、DOE が最適化の前兆となる場合があります。
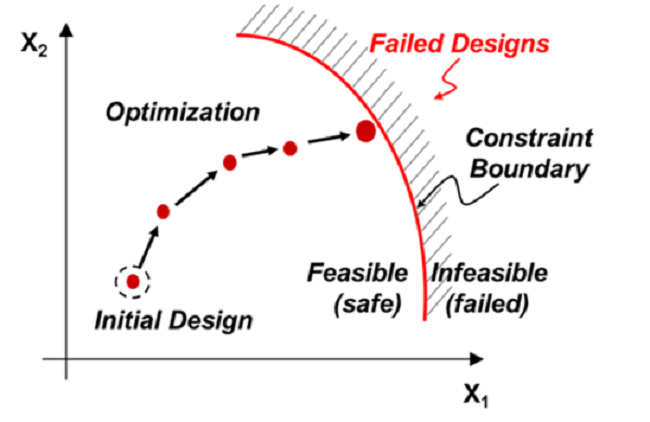
最適化手法の種類
目的関数の定義方法と適切な設計空間のタイプに応じて、それらを分類するさまざまな方法があります。
制約のあるテクニック: これらは、動作するために別々の関数を使用し、1 つは目的用、もう 1 つは制約用です。 私たちは皆、エンジニアリングの授業中にこのようなテクニックをある程度見たことがあります。 最も一般的なものです。
x1>x>x2 で F(x) を最小化/最大化します
条件: h(x)>a1; g(x)>a2; f(x)=0など
制約のないテクニック: 目的と制約の両方に 1 つの関数だけを使用します。 ユーザー定義の制約は目標とは別に定義されていますが、内部的には制約付きの問題が制約なしの問題に変換されます。
さまざまなタイプの設計空間への適用に基づいて、最適化方法は、勾配ベース、直接、または探索に分類できます。 以下の図に示されている略語は、各カテゴリのメソッドの名前です。
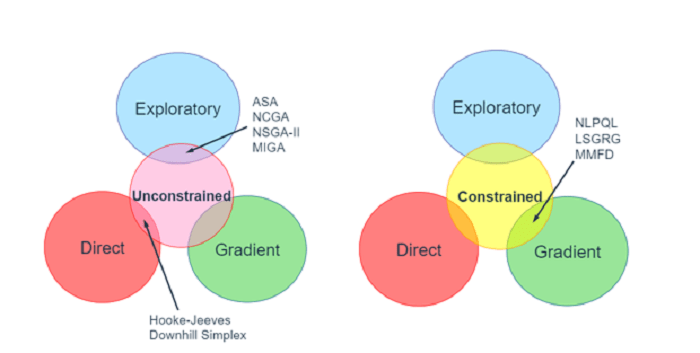
グラデーション法: これらは最も古く、業界で十分にテストされています。 これらは、最小エネルギーまたは最大安定性の原則に基づいて動作します。 ボールを谷にそっと落とすと、ボールは最も急な下り坂に沿って滑り、付近の最低点に達します。 これらの方法は、C0 と C1 の連続性を持つ連続設計空間で機能します。 極小点で行き詰まる可能性が高いため、最初の点は慎重に選択する必要があります。

直接的な方法: 直接検索アルゴリズムは基点から始まります。 周囲の一連の点を検索し、目的関数の値が現在の値よりも低い点を探します。 アルゴリズムは、新しい基点としてその点にジャンプし、その周囲の新しい点のセットを検索します。 このような方法は勾配計算が必要ないため、計算効率が高いことがわかります。 C0 と C1 の連続性が必要ないため、より汎用性が高くなります。 最も一般的なものはフックス・ジーブスとダウンヒル・シンプレックスです。
フックのジーブス法は、その進行方向を追跡します。 進行方向に低い点がある場合、ステップごとに方向は変わりません。

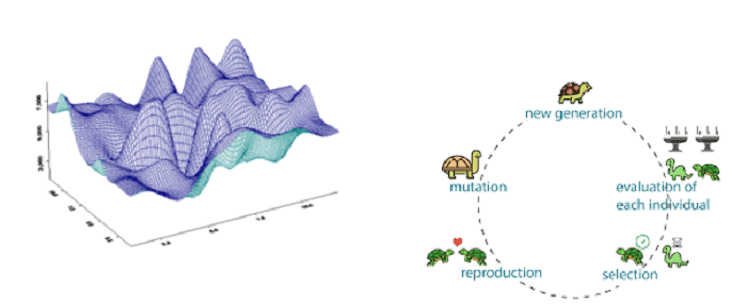
探索的手法: これらの方法は、親と呼ばれる点の 1 つのデータ セット間の交叉または突然変異技術に基づいて、子と呼ばれる別の点のデータ セットを生成します。 新しいデータセットは変異のたびに進化し、最適なソリューションに近づきます。 これは、あらゆる種類の目的関数 (以下に示すように、不連続、微分不可能、確率的、混合整数型、および複数の山と谷を持つ高度に非線形) で機能する高忠実度のスキームです。 ただし、これは計算コストの点で最も高価な最適化スキームです。 最も一般的な方法は、遺伝的アルゴリズム、粒子群、適応型シミュレーテッド アニーリングです。
ポインタベースのメソッド: これは、ユーザーが適切な精度で問題を解決するためにどのタイプの手法が最適であるか見当がつかない場合に備えて、組み合わせて使用するアプローチです。 ポインターによるアプローチは、ユーザーが視覚化するのが難しい見慣れないタイプの設計空間に遭遇したときに役立つ可能性があります。 ポインタ法では、最大 3 つの最適化スキームを利用できます。できれば各バスケットから 1 つずつ、勾配、直接、探索的最適化スキームを使用できます。 最適化が進むにつれて、アルゴリズムは各方法の有効性を追跡し、特定の問題に最も適した方法を使用します。
デザイナーのためのフォーラムに参加しよう
あなたの専門知識はコミュニティにとって不可欠です。私たちに参加して、あなたの知識を提供してください。
今すぐフォーラムに参加する業界最高のプロフェッショナルと分かち合い、学び、成長する.

