デザイナーのためのフォーラムに参加しよう
あなたの専門知識はコミュニティにとって不可欠です。私たちに参加して、あなたの知識を提供してください。
今すぐフォーラムに参加する業界最高のプロフェッショナルと分かち合い、学び、成長する.
概要
このディスカッションシリーズの最初のパートでは、剛体表面に物体を落下させ、その衝撃期間中にどのようなたわみと応力が発生するかについて、手作業による計算と時間依存応答との関係を探り、検証しました。 以下で説明する概念は、ANSYS Mechanical を使用して過渡構造解析をセットアップして解く方法を理解する上で不可欠です。
図 1:衝突時の棒(たわみのスケールを誇張して表示).
図 1 は、落下後の棒の例を示しており、衝撃の間に何が起こったかを示しています。 この資料の残りの部分では、この種のシステムをどのようにセットアップして解析し、一般的な手計算と比較することができるかについて説明します。
以下は、このディスカッションで取り上げられるトピックのリストです(登場する順):
- 位置エネルギー
- 弾性エネルギー
- 方向剛性
- 静的構造解析
- 平均圧縮力
- 運動エネルギー
- 衝撃速度
- 衝撃周期
- 固有振動数
- モーダル有効質量
- 過渡構造解析
- 解析期間
- タイムステップ頻度
- 複雑な過渡変位と応力の結果
- 平均圧縮応力
詳細
私は、ある物体が別の物体に衝突するような動的な事象によって生じる最大たわみと応力の結果と、手計算との関係を探求し始めました。 ANSYS Mechanicalを使用して、仮定を検証し、これらの動的事象の詳細を明らかにしました。 私は有限要素法を信頼しており、私の発見を皆さんと共有できることを楽しみにしています。
私は、円柱状の棒を剛体表面に落下させるという単純な例から調査を開始しました。 このシナリオ、およびこの議論に関連するすべてのシナリオでは、弾性的な材料挙動があり、どの荷重も塑性変形や損傷を起こさないと仮定しています。 これは、形状内にエネルギー保存があることを意味します。
このプロセスで、私は一連の仮定を立て、有限要素解析を実施して、それらの仮定を検証したり、異議を唱えたりしました。 このプロセスによって、私はさらに多くの質問をし、分析し、答えを得ることができました。 最終的に、私はこのダイナミックな出来事の多くの側面を自信を持って説明できるようになりました。
最も単純なアイデアから始めましょう。
この最初の例では、円筒形の棒を硬い表面に落とすことを考えます。 棒の直径は25.4mm、長さは254mm、質量密度は7.85e-06です。 [kg/mm³]. この棒は底面から1mの高さから落とされます。
図2:円柱棒
この状況では、位置エネルギーは弾性エネルギーに等しくなければなりません。
位置エネルギー:

弾性エネルギー:

落下する円柱の位置エネルギーと弾性エネルギーを等しくして、たわみを正確に予測できるかどうかを調べてみましょう。
棒は負のY方向に移動するように落下すると仮定します。 したがって、最初のステップは、Y方向のジオメトリの剛性を決定することです。
私たちのモデルの場合、この剛性は理論的に導き出すことができます。また、有限要素法を使って既知の荷重をかけ、この荷重を計算されたY方向のたわみで割ることによっても導き出すことができます。 これにより、有限要素法による推定結果を理論的に導き出された値と比較することができ、私たちの方法論に対する信頼性を高めることができます。
理論的な剛性を導き出しましょう。 Y方向については、以下の式が適用されます:

ここで、異なるタイプの荷重に関係する異なる考慮事項を理解するために、2つの異なる方法で有限要素解析による形状剛性も計算してみましょう。
ここでは、シリンダーの遠位端に力を加えながらベースを固定し、ベースでの反力がシリンダー上部に加えられる力と大きさが等しく符号が反対になるように考えます。 この圧縮荷重の大きさは、材料特性が線形であり、形状の非線形性(大変形)を考慮しない限り、重要ではありません。
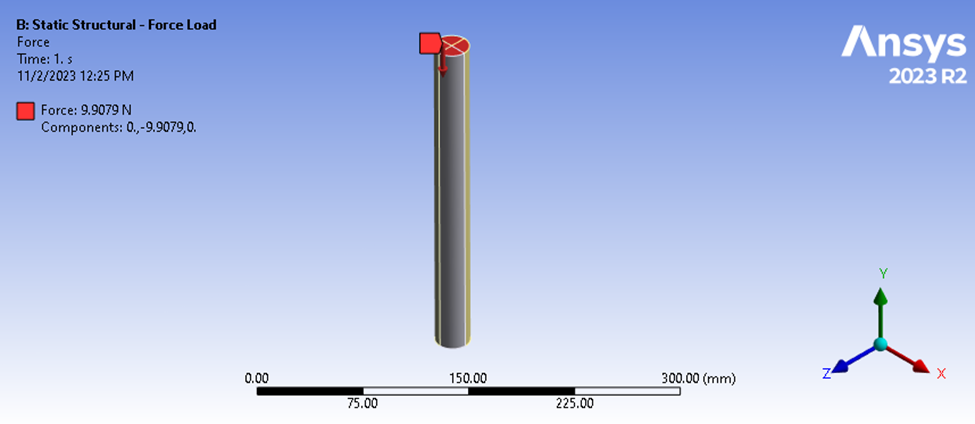
図3: 上部から荷重を受け、下部で支持されたロッドの静的構造解析。
このシナリオでは、上面に9.9079 Nの荷重がかかり、下面はY変位から固定されています。 この荷重の大きさは後ほど詳しく説明します。
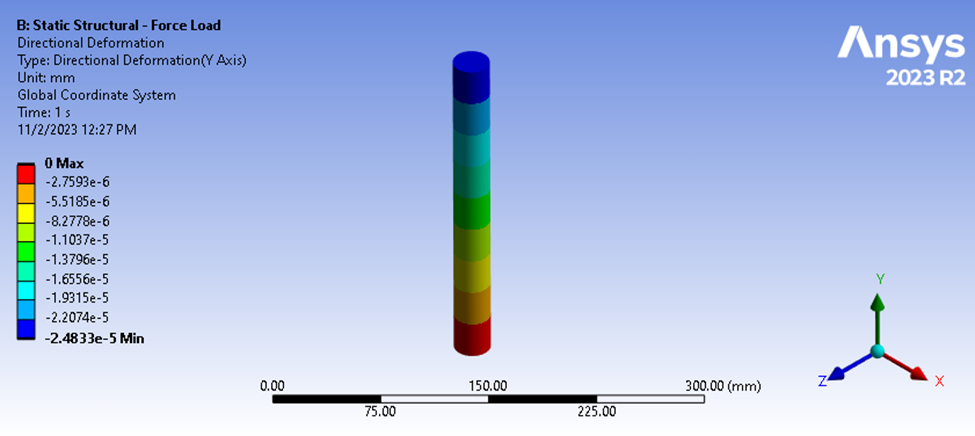
図4:静的構造のたわみ結果
静的構造解析を解くと、圧縮たわみの最大値は 2.4833e-5 mm であることがわかります。 9.9079 N の荷重に基づいて、以下の平均剛性を計算できます。
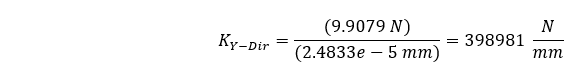
有限要素法は理論的アプローチと0.00125%しか差がないことがわかります。 これにより、私たちは良い気分になります😊。
次に、重力荷重のような異なるタイプの荷重を考えてみましょう。 ここでは、上面から力を取り除き、下面は拘束したまま、9806.6mm/sec^2で重力をかけます。 底面の反力は9.9079Nですが、上面に作用する力はほぼ間違いなくゼロです。 たわみの結果は、1.2421e-5 mm という異なるたわみの大きさを示しています。
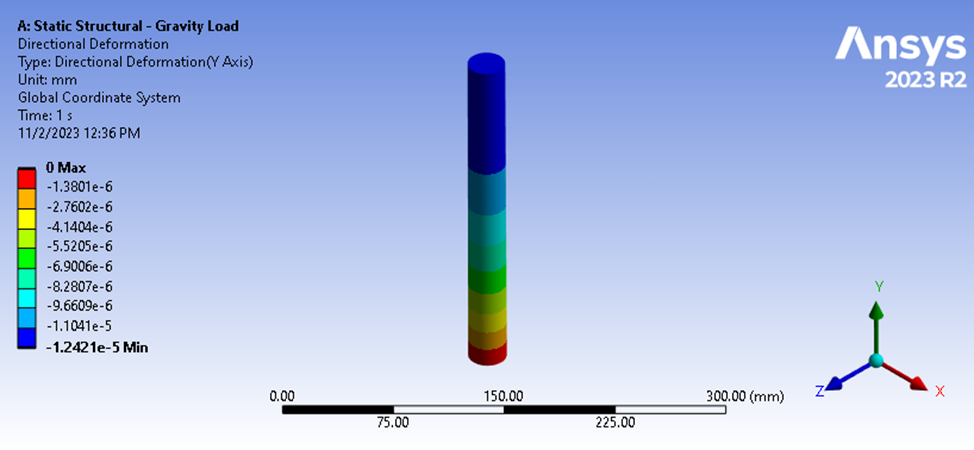
図 5:静的構造解析のたわみ結果
上記と同じ式の形で剛性を計算しようとすると、形状に作用する平均圧縮力を考慮していないため、誤った値になります。 この場合、形状が一定の断面を持つため、平均圧縮力は簡単に推定でき、推定平均剛性は以下のように計算できます。
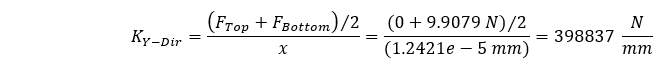
この推定値は、理論的に計算された値との差が0.0348%であることを示しています。 したがって、2つの異なる荷重方法によって、形状方向の剛性を自信を持って推定することができます。
推定された方向剛性をモデルおよび材料特性と共に代入すると、以下のように最大たわみを推定することができます。
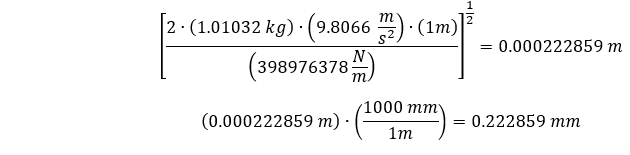
これは約0.223mmです。 次に、円柱棒が地面に衝突した時と衝突後のたわみをシミュレートする過渡構造モデルが必要です。

図6:過渡構造解析モデルと制約条件
このモデルでは、棒が負のY方向に4428 mm/secで移動すると仮定しています。 これは、このバーが1m落下した場合に達成する速度です。この速度は、シャフトの位置エネルギーと衝突の瞬間の運動エネルギーを等しくすることで計算できます。
運動エネルギー:
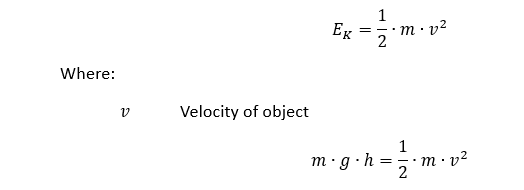
ですから

ジオメトリの垂直方向の高さを維持するために制約が追加され、ベースには圧縮のみのサポートが追加されます。 解析期間は、結果を収集するための頻繁なキャプチャレートとともに定義されます。
衝撃の後、バーの上部が下方にたわむと、圧縮のみのサポートに関連する剛性によってバーの下部がわずかに圧縮される可能性があるため、解析結果は複雑になります。 バーの全体的な圧縮を表すのは、これら 2 つの面の間のたわみの差です。
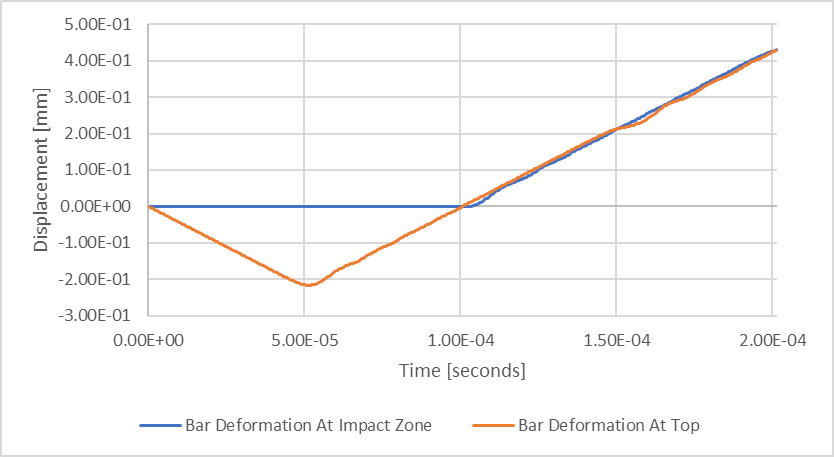
図 7:過渡構造たわみの結果
青い線の平坦な期間、「衝撃ゾーンでのバーの変形」は、底面での接触が発生する期間、つまり衝撃に関連する滞留期間を示しています。 この期間に着目してデータを再プロットすると、いくつかの観察がより容易になります。
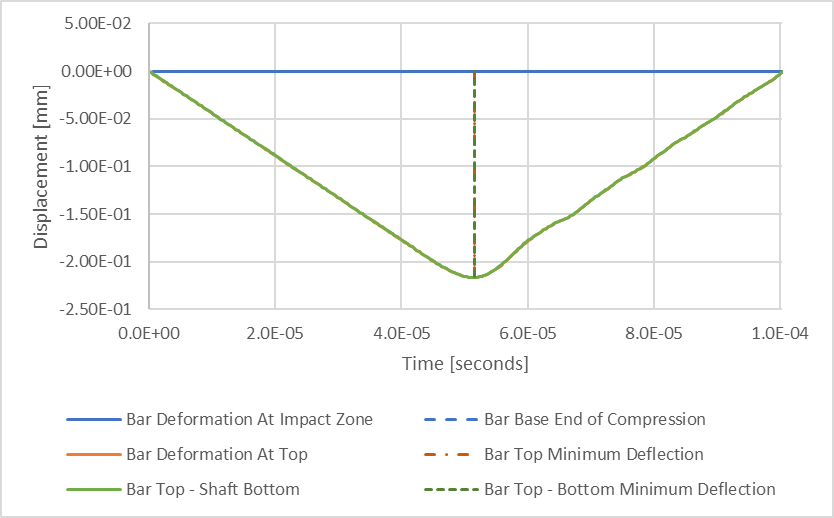
図 8:過渡構造圧縮たわみの結果
バーの上面たわみと下面たわみの差を表す緑色の線を追加しました。 2本の垂直破線は、オレンジと緑の線の最小結果に関連する時間間隔を表しています。 棒の最小圧縮は、棒の上面の最小圧縮と同時に起こることがわかります。 このことから、バーの最大圧縮は0.216 mmと推定でき、これは推定最大たわみ0.223 mmより3%弱小さい値です。
しかし、この例とその結果から探求し、学ぶべきことはまだあります。
ここでは、過渡構造解析の設定という側面から、特に今回の事象に関連する時間周期を取り上げ、どのような形状に対してこの周期をどのように見積もることができるかを判断してみましょう。
青い線が負の変位から正の変位に交差した時間(0.00010026秒)を見てみると、これはシャフトの圧縮に関連する周期に等しくなります。
シャフトは弾むバネと考えることができます。 衝撃の持続時間は、圧縮方向の固有振動数の周期の 1/2 を反映しています。 したがって、次のようになります。

では、この理論を裏付けることができるかどうか、また、このような形状や、将来解析したいと思うような形状の固有振動数をどのように推定できるかを探ってみましょう。
上記のテストモデルに適用された「圧縮のみ」のサポートを変更し、同じサーフェスにY方向の拘束を加え、ANSYSで縦振動周波数を直接解くことができます。
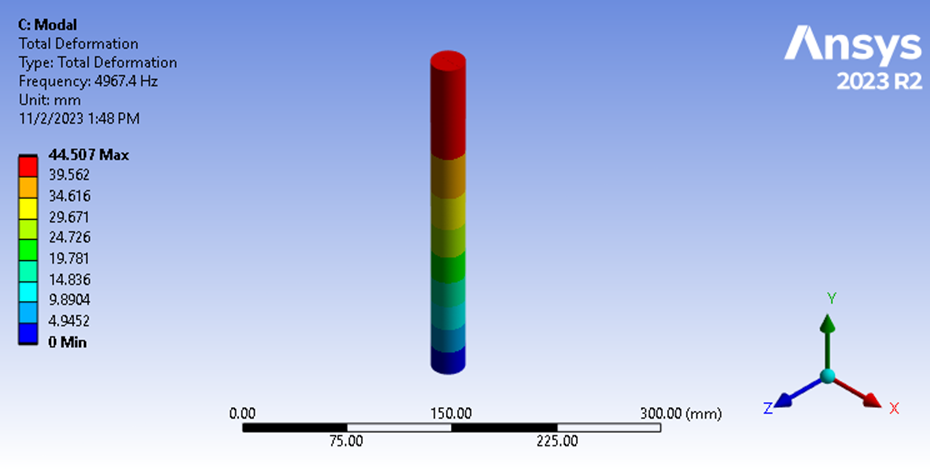
図 9:モーダル解析の基本周波数
縦振動数は 4967.4 Hz です。 これは、過渡構造変位の結果に基づく固有振動数の推定が、0.4%以内の精度で行われたことを示しています。 この所見は、2つの物体が衝突した場合の衝撃の持続時間は基本周波数の周期の1/2に等しいという私たちの理論を裏付けるものです。
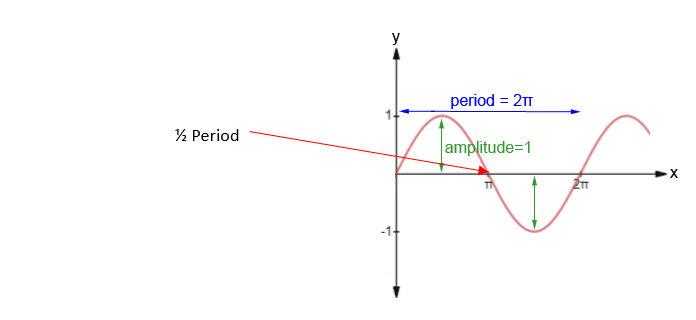
図 10:衝撃の周期
この解析例では、部品は1つしかなく、圧縮のみの垂直サポートがもう1つの非常に硬い物体を表していると仮定します。 したがって、このシャフトは、これら 2 つの衝撃を受ける相手のうち、より柔軟な方です。 この過渡構造解析では、解析期間をこの固有振動数の周期に等しく定義し、この周期の最初の1/2の期間に衝撃が発生することを想定しています。
しかし、過渡構造解析を設定する場合、この固有振動数をどのように計算するのでしょうか?
先ほどお見せしたように、衝撃姿勢を維持するための拘束条件を使用しながら、形状のモーダル解析を実行し、衝撃圧縮のモード形状を直接解くことができます。 しかし、同じことを達成する解析的な方法はあるのでしょうか。
これを調べるには、衝撃方向における形状の固有振動数を計算する必要があります。

方向剛性を推定する方法についてはすでに説明しましたが、モード有効質量の考察をよりよく理解するために、いくつかの例を考えてみましょう。
このシステムの全質量は
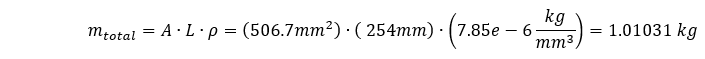
ジオメトリの一端が拘束されているため、系の有効質量は全質量よりも小さくなります。 ジオメトリの複雑さと、ジオメトリを固定するために使用される拘束に基づいて、参加する質量の量を見積もるのは難しいかもしれません。 私たちの場合、形状は単純であり、一端が固定された押し出し断面の場合、有効質量はシステムの全質量の1/3に等しいと導かれることがよくあります。 この場合、基本周波数は次のようになります:
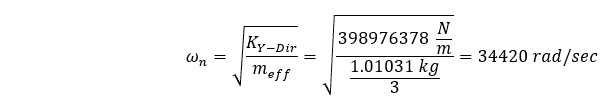
これは、より明確に次のように表現できます:
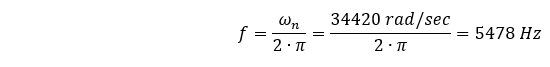
この値(5478Hz)は、有限要素法で計算した固有振動数(4967.4Hz)よりも10%以上大きいのです。
答えはモーダル有効質量の推定に関係しています。 縦剛性の計算に自信があれば(…あります…)、モデルの設定を変更して、基本周波数の計算をより簡単に検証することができます。
モデルの材料の質量密度をゼロに設定し、ジオメトリの遠位端に1.01031kgの質量を追加します。
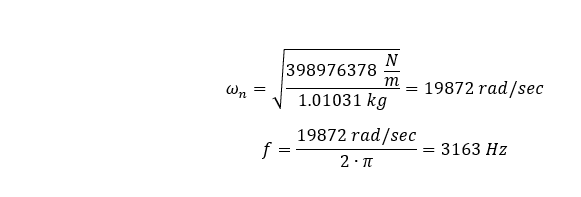
有限要素解析を実行した結果、基本縦振動数は3154.6Hzであることがわかりました。
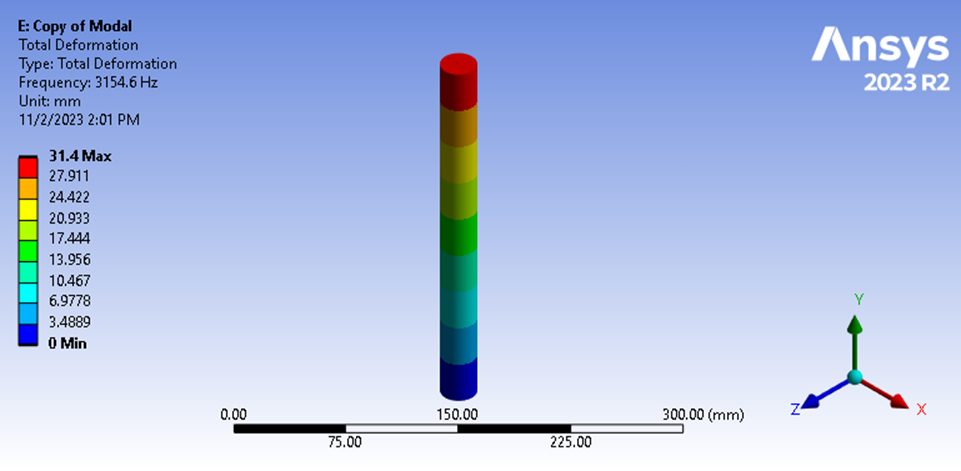
図11 モーダル解析の基本周波数
これは、手計算との0.27%の差を反映しています。 したがって、有限要素法に対する信頼性が増し、形状全体に分散した質量を利用した手計算で使用した有効質量の見積もりの弱点が明らかになりました。
式を再整理することにより、分布質量を考慮しながらANSYSで計算された固有振動数を考慮して、この有効質量を次のように解くことができます:
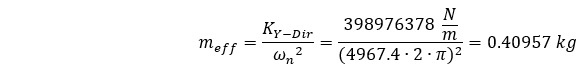
この有効質量は、システムの全質量の0.405であることがわかります。
したがって、他の、より複雑な形状の場合、この質量分率は一意であり、理論的に導出するのは困難であり、有限要素法を使用して固有振動数を確実に解くことができると予想されます。
与えられた形状に対して固有振動数をどのように決定するかを理解したところで、過渡解析中にどの振動数で解析結果を収集すべきかを決定する必要があります。
そのためには、解析ステップサイズが解析にどのような影響を与えるかを、2つの異なる観点から検討する必要があります。 1つは、正弦波のような非線形応答の区分的線形特性を使用して期待される観点です。 もう1つの観点は、実際の解析結果が捕捉率周波数の変化の関数としてどのように変化するかということです。 私たちは衝撃問題を検討しており、衝撃周期は柔軟なコンポーネントの基本振動に関連していると仮定しているため、ステップサイズと、それが正弦曲線を表現する精度にどのように影響するかとの関係を調べることは理にかなっています。
この関係を評価するために、正弦曲線の前半の大きさの加重平均を、この同じスパンの理論的平均と比較します:
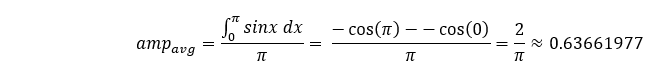
次に、異なるステップ数を使うことによって、この正弦曲線をどの程度正確に表現できるかを調べ、台形の法則を使って前半の曲線の下の面積を計算し、その面積をそのスパンの周期で割ります。
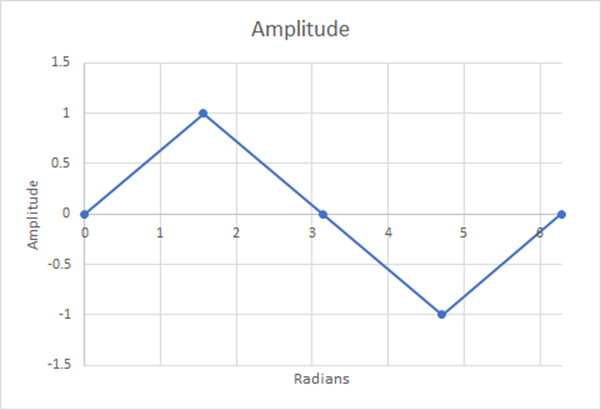
図12:4ステップ;推定加重平均=0.5;21.46%の差
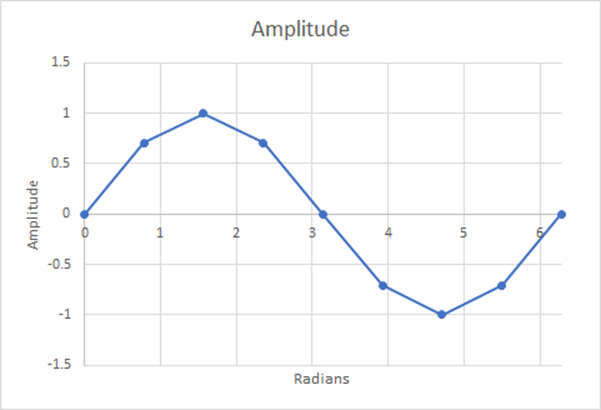
図13:8ステップ;推定加重平均=0.60536;5.19%の差
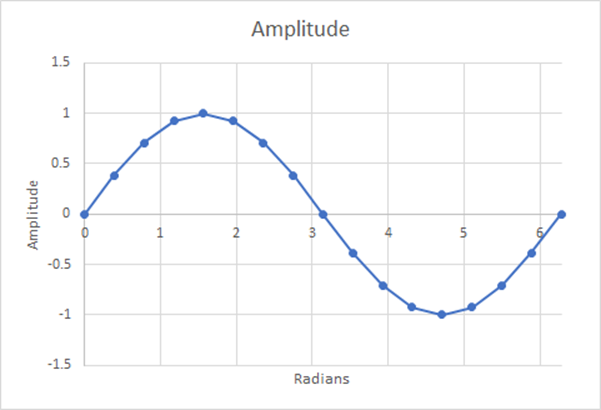
図14:16ステップ;推定加重平均=0.6284;1.29%の差
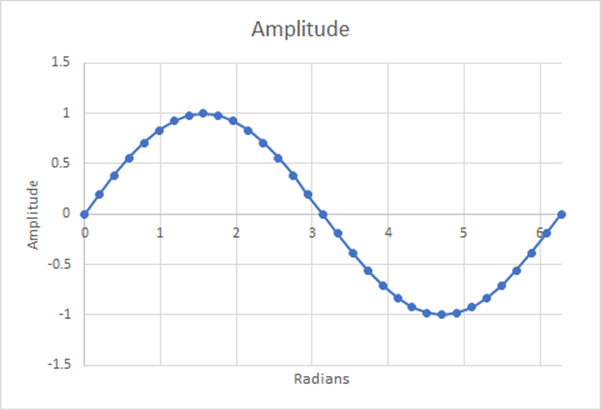
図15:32ステップ、推定加重平均=0.6346、差0.32
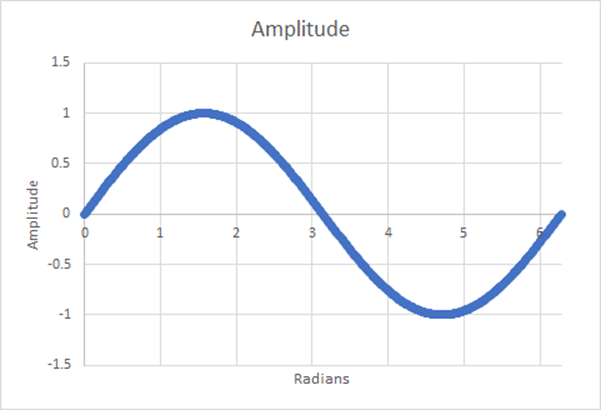
図16:512ステップ、推定加重平均=0.6366、0.001%の差
実際、理論値と完全に一致することはなく、この精度が時間ステップ数の増加に伴ってどのように変化するかをプロットすると以下のようになります。
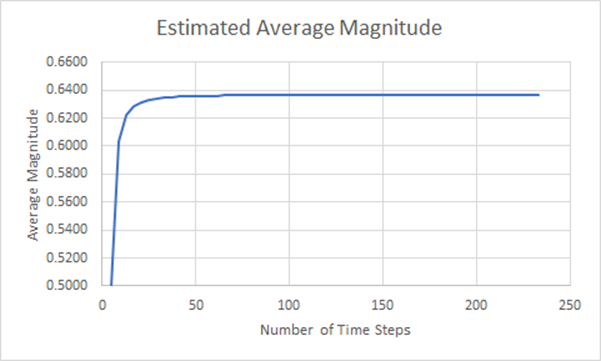
図17:推定平均マグニチュード収束プロット
この検証から、近似のステップ数を増やすとすぐに精度が大きく向上することがわかります。 しかし、これは時間ステップ数が増加するにつれて結果がどのように変化するかは考慮していません。
解析結果への影響を調べるために、解で定義された異なるタイムステップ数を考慮しながら、最大ロッド圧縮結果を時間の関数としてプロットします。
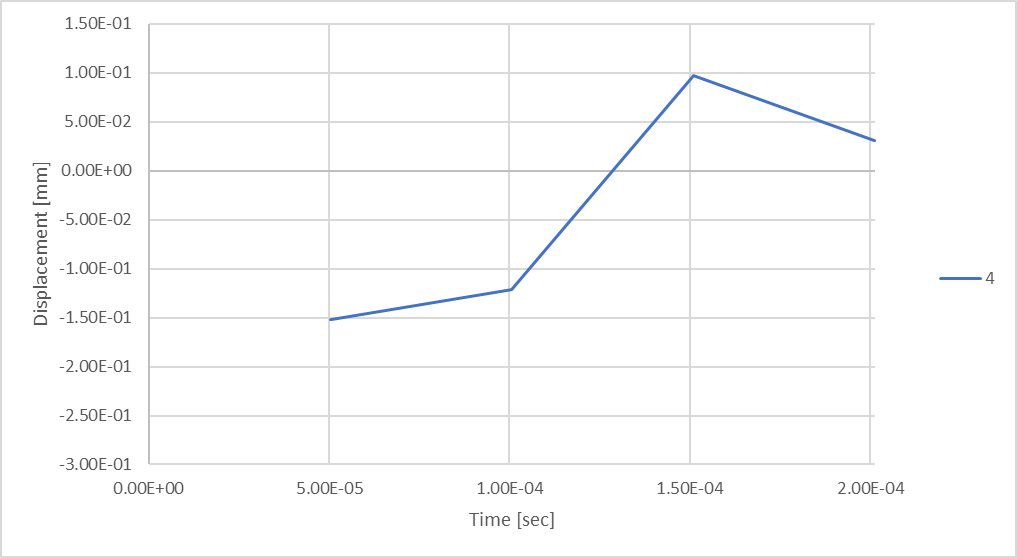
図18:4つのタイムステップを考慮した場合のロッド変位。
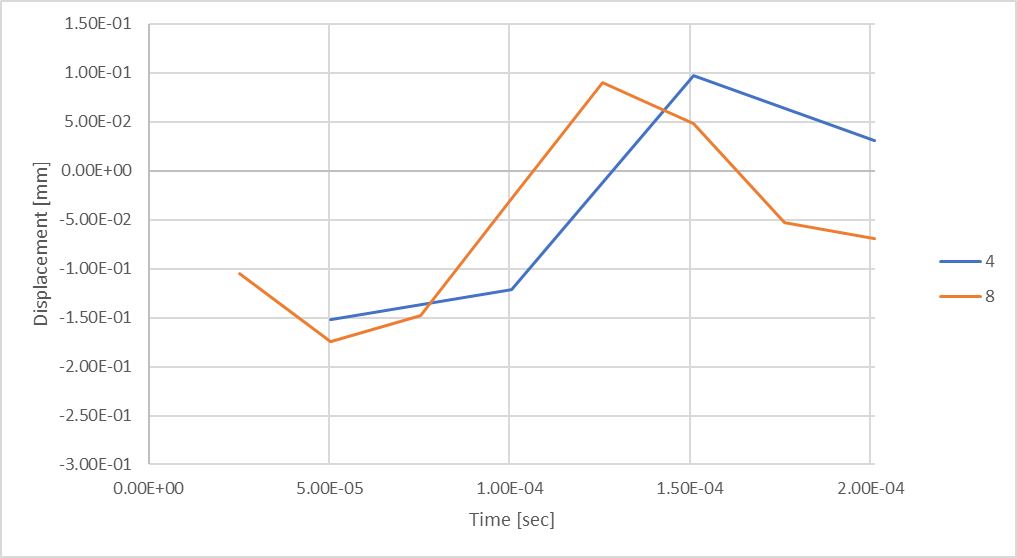
図 19: 8 タイムステップを考慮したときのロッドの変位.
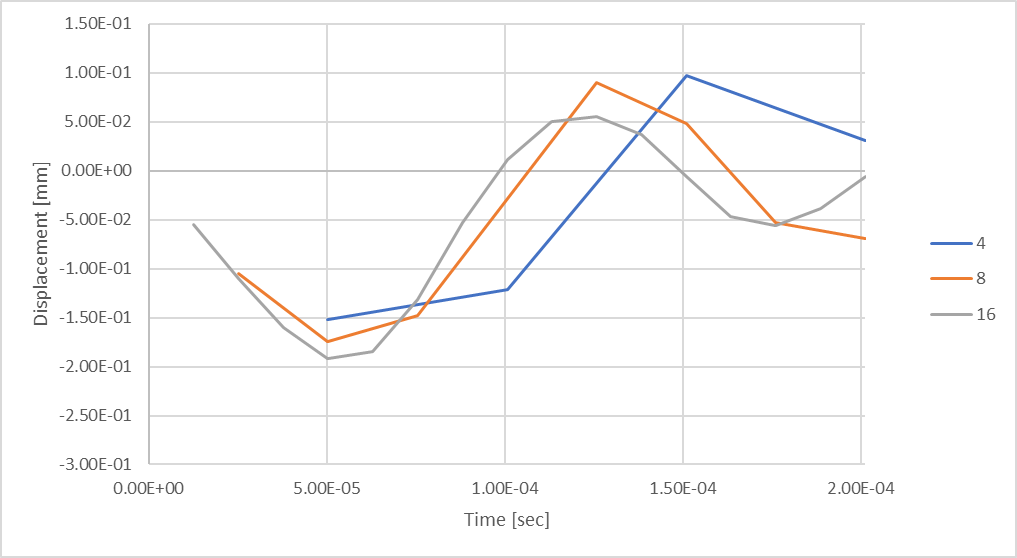
図20: 16タイムステップでは、ロッドの圧縮変位が大きくなっています。
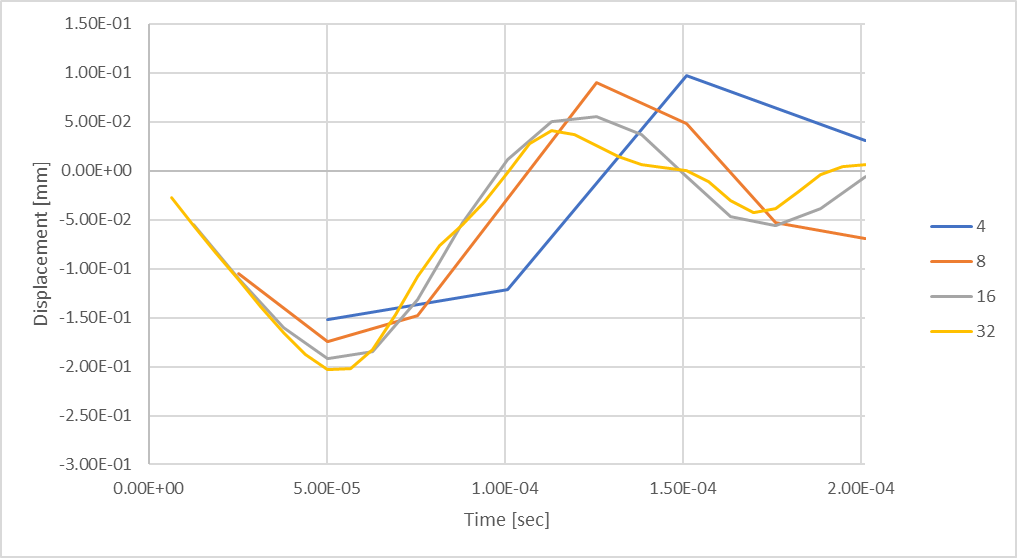
図 21: 32 タイムステップを使用した過渡最大ロッドたわみ。
平均的な正弦波の大きさを計算する事前の解析に基づき、32ステップを考慮することで、理論結果と最大0.32%の差が予想されることがわかりました。 しかし、私たちのロッド圧縮変位応答は、事前の時間ステップの探索と比較して、まだ形成されていることがわかります。 さらに時間ステップを増やすとどうなるでしょうか?
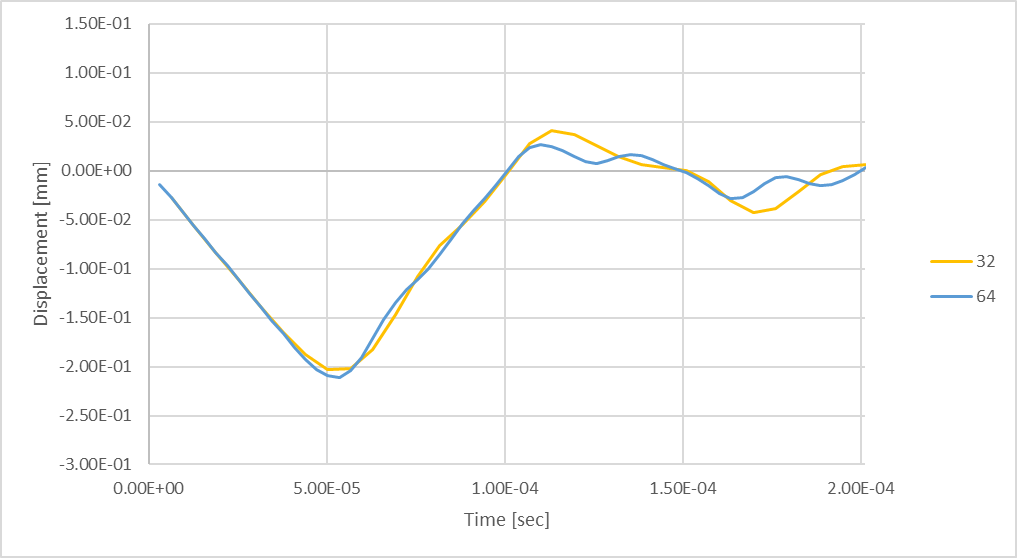
図 22:64 個のタイムステップを使用した過渡最大ロッドたわみ。
64 回のタイムス テップでは、ロッドの最大圧縮たわみがわずかに大きくなりますが、ほぼ同 じです。
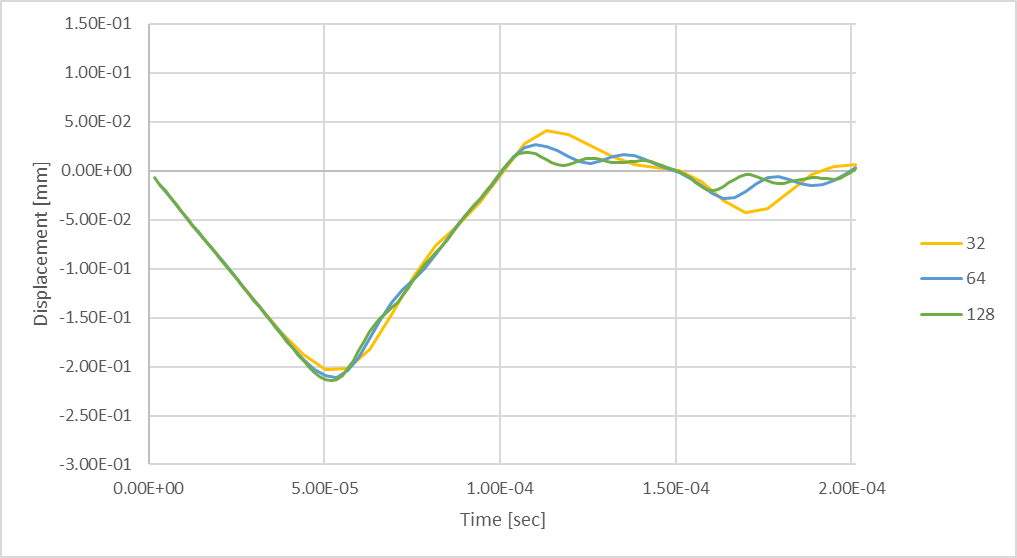
図 23:128タイムステップを使用した過渡最大ロッドたわみ。
128 回のタイムス テップを考慮すると、少ないタイムス テップ数よりもシャフトのピークの圧縮 が大きくなります。 最大圧縮たわみは、32 のタイムス テップを考慮した場合よりも 6%大きくなっています。
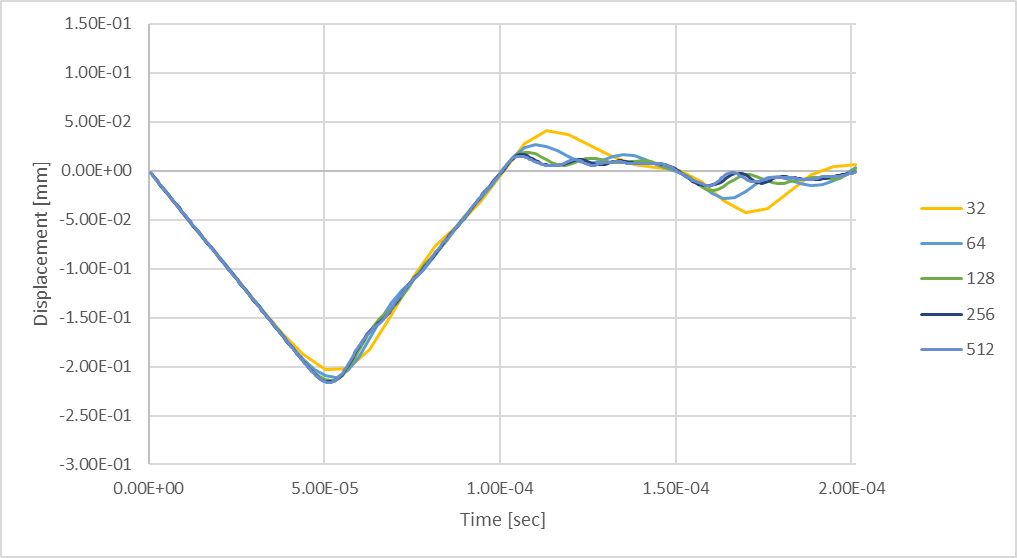
図 24:最大 512 のタイムステップを使用した過渡最大ロッドたわみ。
256 回のタイムステップ解析結果と、512 回のタイムス テップを考慮した解析結果を比較すると、より多くのタイムス テップを考慮することで、動的応答のさらなる分解能を計算で きることがわかります。 次の図は、過渡構造解析で考慮するタイムス テップ数の関数として、ロッドの最大圧縮たわみがどのように変 化するかを示しています。
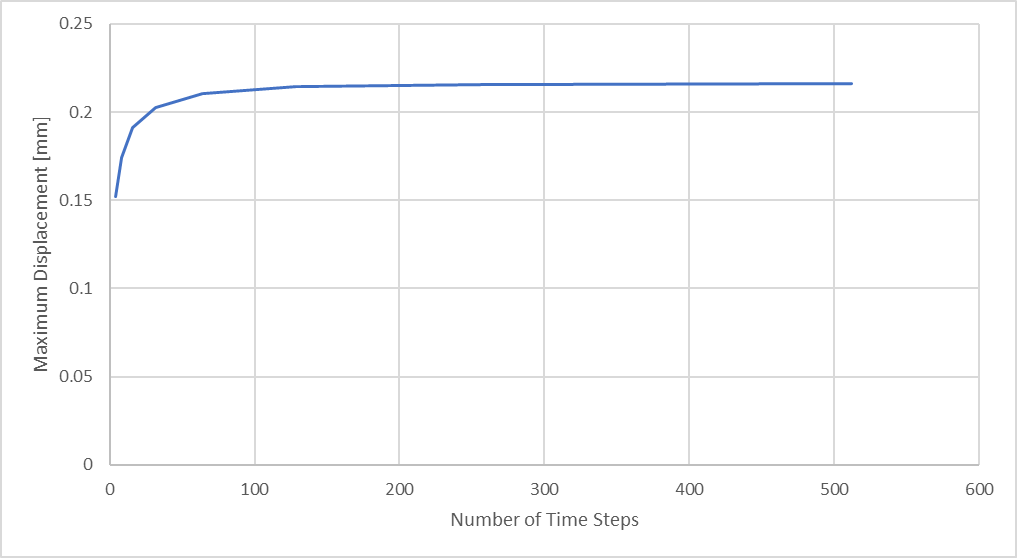
図 25:ロッドの最大圧縮変位と解析時間ステップ数
最終的に,あるメッシュサイズでは,解析時間の延長と解析結果ファイルの増大に伴う労力が結果の大きさの大きな変化によって正当化されないという収穫逓減のポイントに到達します.
これら 2 つの考察に基づき、32 個のタイムス テップを使用することで、正弦曲線を最大 0.32% の差で特徴付けることが期待できますが、512 個のタイムス テップを使用した同じ解析と比較して 94% の精度でしか変位結果を得られず、理論上の最大たわみと比較して 91% の精度しか得られないことがわかります。 下図は、ロッド圧縮の最大値と理論的に推定された最大値を比較したものです。
| サブステップ数 | 最大圧縮 | 理論上の最大 | 差 |
| 4 | 0.152139 | 0.222859 | 31.73% |
| 8 | 0.174023 | 0.222859 | 21.91% |
| 16 | 0.191486 | 0.222859 | 14.08% |
| 32 | 0.202746 | 0.222859 | 9.03% |
| 64 | 0.210712 | 0.222859 | 5.45% |
| 128 | 0.214455 | 0.222859 | 3.77% |
| 256 | 0.215752 | 0.222859 | 3.19% |
| 512 | 0.216232 | 0.222859 | 2.97% |
図 26:最大ロッド圧縮変位 vs 解析時間ステップ
時間ステップの数を増やすと,有限要素解析の結果と理論的に導出された値との一致度が高くなります.
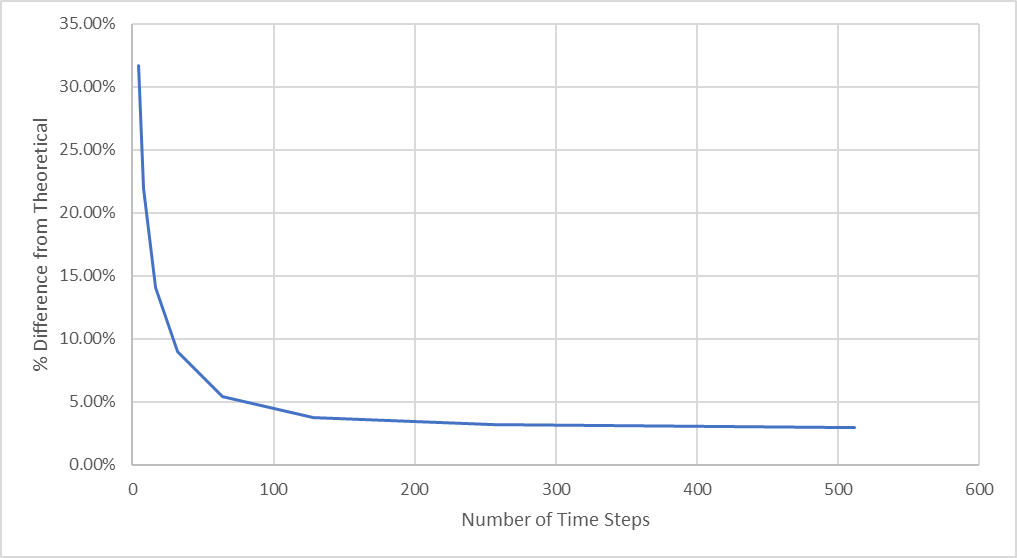
図27:理論上の最大たわみとの差の割合
この図から、時間ステップ数が64から128の間になると収束に向けて劇的な改善が見られますが、時間ステップ数を増やしてもほとんど変化しないことがわかります。
しかし、ストレスのような他の結果に関して、これは何を意味するのでしょうか?
以下に、いくつかの解析シナリオについて、時間あたりの最大フォンミーゼス応力をプロットしてみます。
図28: 32時間ステップを解いたときのフォンミーゼス応力
図29:64時間ステップを解いたときのフォンミーゼス応力
図30:128時間ステップを解いたときのフォンミーゼス応力
図31:256時間ステップを解いたときのフォンミーゼス応力
図 32: 512 時間ステップを解いたときのフォンミーゼス応力
まとめると、これが応力を表示しているときのものです:
| サブステップの数 | 最大平均応力 | 最大ピーク応力 | 平均応力差 |
| 4 | 120.04 | 301.98 | 29.62% |
| 8 | 136.4 | 316.61 | 20.03% |
| 16 | 150.57 | 312.42 | 11.72% |
| 32 | 159.15 | 301.68 | 6.69% |
| 64 | 165.4 | 283.51 | 3.03% |
| 128 | 168.84 | 303.99 | 1.01% |
| 256 | 170.05 | 354.35 | 0.30% |
| 512 | 170.56 | 442.08 | 0.00% |
図 33:最大ロッド圧縮変位 vs 解析時間ステップ
ピーク衝撃応力は、時間ステップ数が増加するにつれて大きくなり、衝撃の開始時に最大値を示し、イベント全体を通じて小さくなっていることがわかります。 ロッドの平均応力は、ゼロから最大圧縮時のピークまで上昇し、 衝撃終了後にゼロに向かって下降します。 これらの最大平均応力を以下にプロットします。
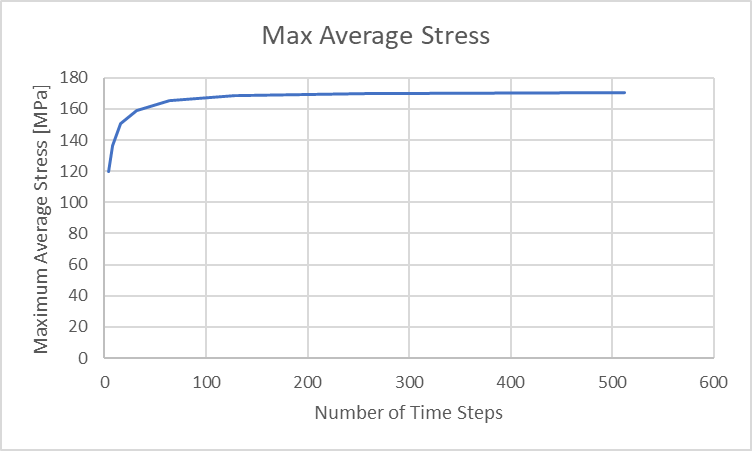
図 34:最大ロッド圧縮変位 vs 解析時間ステップ
これらの最大平均応力を考慮するために、ロッドの理論的な最大平均応力を次のように計算することができます:
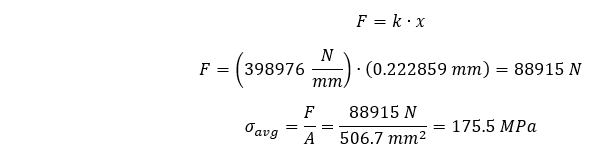
最大平均応力と理論的に計算された最大平均応力をプロットし直すと、その差は次のようにまとめられます:
| サブステップ数 | 最大平均応力 | 理論上の最大平均応力 | 差 |
| 4 | 120.04 | 175.5 | 31.60% |
| 8 | 136.4 | 175.5 | 22.28% |
| 16 | 150.57 | 175.5 | 14.21% |
| 32 | 159.15 | 175.5 | 9.32% |
| 64 | 165.4 | 175.5 | 5.75% |
| 128 | 168.84 | 175.5 | 3.79% |
| 256 | 170.05 | 175.5 | 3.11% |
| 512 | 170.56 | 175.5 | 2.81% |
図 35:最大ロッド圧縮変位 vs 解析時間ステップ
再び、たわみの場合と同様に、事象に対して 64 から 128 の時間ステップを考慮した場合、理論的に計算された最大平均応力と比較して、最大平均応力の差のパーセンテージが大幅に改善されました。 しかし、より多くの時間ステップを使用しても、結果の精度はほとんど向上しません。
結論
硬い表面への弾性体の落下のような動的事象の最大たわみと平均応力を推定するために使用されるエネルギー法は、妥当な結果をもたらす可能性があること、そして、最も顕著な精度の向上は、衝突方向について計算された、衝突する物体の固有振動数と同じ周期の事象について64から128の時間ステップを考慮する間に生じることを検証しました。 また、この固有振動数を近似する最良の方法は、手計算ではなく、有限要素法を用いたモーダル解析であることもわかりました。
デザイナーのためのフォーラムに参加しよう
あなたの専門知識はコミュニティにとって不可欠です。私たちに参加して、あなたの知識を提供してください。
今すぐフォーラムに参加する業界最高のプロフェッショナルと分かち合い、学び、成長する.

