디자이너를 위한 포럼에 참여하기
여러분의 전문 지식은 커뮤니티에 매우 중요합니다. 참여하여 지식을 공유하세요
지금 포럼에 참여하세요업계 최고의 전문가들과 함께 공유하고 배우며 성장하세요.
요약
다물체 동역학(MBD)을 사용할 때는 해석하는 데 너무 오랜 시간이 걸리지 않는 모델을 설정하는 것이 중요합니다. 이를 달성하는 가장 좋은 방법은 강체를 사용하는 것입니다. Ansys Motion에는 일부 유연한 부품이 필요한 경우 본체의 응력을 계산하는 두 가지 옵션이 있습니다. 하나는 전체 유한 요소 공식을 활용하는 Nodal 접근 방식이고 다른 하나는 모달 선형 확장을 사용하는 Modal 접근 방식입니다. 이 블로그에서는 스트레스 결과의 차이점을 확인하기 위해 이 두 가지 방법론을 비교합니다.
모달 및 노드 분석.
노드 접근 방식을 사용하면 솔버는 모델 내 최대 자유도(DOF) 및 매트릭스 크기를 포함하는 전체 FEA 계산을 수행합니다. 반면, 모달 접근법은 변형 벡터를 가정합니다. 유 모드형상 세트를 선형적으로 결합하여 표현됩니다.
![]()
스케일 팩터 또는 진폭 ㅏ 모달 좌표라고 하며 Ψ 모드 형상의 집합입니다.
변형이 다음과 같이 구축될 수 있음을 알 수 있습니다.

그런 다음 솔버는 먼저 유연한 부품에 대한 모달 해석을 계산하고 계산된 모드를 사용하여 모델을 해석합니다. 이 경우 DOF 수가 상당히 줄어듭니다. 이 방법론은 선형 모델에만 적용됩니다.
모션 모델.
이 예에서는 유압 액츄에이터를 복제하기 위해 다양한 조인트와 모션 기능을 사용하여 유압 굴삭기 어셈블리를 시뮬레이션했습니다. 버킷이 운반하는 무게를 시뮬레이션하기 위해 버킷에 하중이 적용됩니다. 모델은 다양한 접근 방식을 사용하여 해결됩니다. 처음에는 기본 해석 시간을 설정하기 위해 강체가 사용됩니다. 이어서 두 번째 모델에는 절점 접근 방식을 사용하는 5개의 유연체가 포함됩니다. 마지막으로 마지막 모델도 유연체를 활용하지만 전체 FEA 노드 계산 대신 모달 솔루션을 사용합니다.
강체 모델의 경우 계산 시간은 1초 미만입니다. 그러나 이 모델은 응력이나 변형 결과를 생성하지 않습니다.

Nodal 접근 방식을 사용하면 솔루션을 얻는 데 47k 이상의 DOF와 271초가 소요됩니다.
![]()

모달 유연체를 사용하는 분석에는 약 200 DOF가 포함되며 약 5초가 소요됩니다. 이는 전체 FEA 계산의 중요한 차이점입니다.
![]()
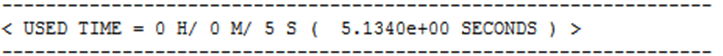
스트레스 결과.
서로 다른 시간 단계 동안의 등가 응력은 두 모델 모두에서 기본적으로 동일합니다. Nodal 모델(오른쪽)에 도달한 최대값은 6.80초에 112.08MPa이고 Modal의 경우 6.72초에 111.96입니다. 스트레스 차이는 0.107%이다.
추가 사항
각 본체 모달 확장에 사용되는 최대 모드 수를 제어하고 첫 번째 모드 형상이 억제되어 솔루션 품질을 향상시키는 방법을 확인할 수 있습니다.
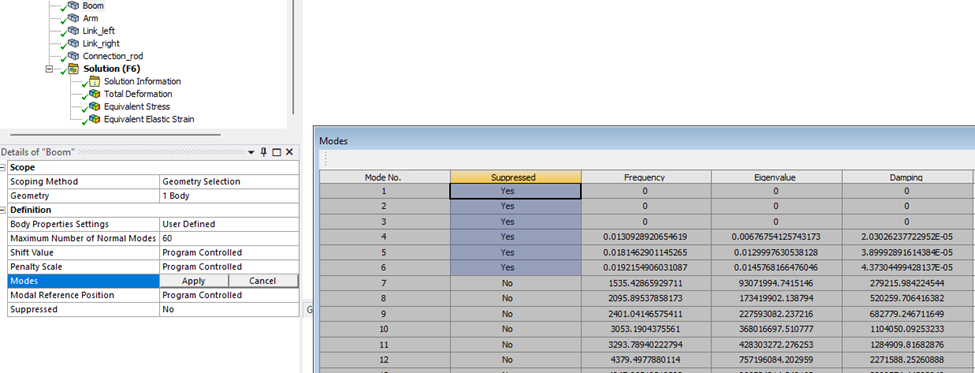
권장 사항
모달 바디에는 비선형 재질을 사용할 수 없습니다. 작은 변형과 선형 재료 가정이 적용되는 경우에만 이 기술을 사용하는 것이 중요합니다.
결론
모달 본체 접근 방식은 신속하게 솔루션을 찾고 일반적인 응력 상태를 확인하는 데 유용합니다. 각각의 특정 사례에 선형 재료를 적용할 수 있는지 여부가 결정되면 사용자는 필요한 경우 노드 분석으로 전환할 수 있습니다.
이 방법을 사용하여 절약한 시간은 예비 설계 단계에서 매우 중요할 수 있습니다. 사용자는 다양한 시나리오를 테스트한 후 가장 유망한 시나리오를 식별한 후 전체 노드 모델로 전환할 수 있습니다.
디자이너를 위한 포럼에 참여하기
여러분의 전문 지식은 커뮤니티에 매우 중요합니다. 참여하여 지식을 공유하세요
지금 포럼에 참여하세요업계 최고의 전문가들과 함께 공유하고 배우며 성장하세요.

