Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.
De twee-condensatorparadox is een provocerend gedachte-experiment dat is opgezet om enkele beperkingen van het modelleren van elektrische circuits bloot te leggen, en er zijn veel verschillende manieren bedacht om de paradox op te lossen. Ik zal een oplossing aan de mix toevoegen die in COMSOL Multiphysics gemodelleerd kan worden.® software en deze vervolgens uit te breiden om een nog provocerendere vraag te stellen en te beantwoorden: Bestaan capaciteit en inductie? Laten we erin duiken!
De twee-condensator paradox
Dit gedachte-experiment wordt gewoonlijk als volgt voorgesteld: Beschouw een apparaat dat bestaat uit twee gelijkwaardige condensatoren, met capaciteit, C, parallel geschakeld met een open schakelaar ertussen. Alle draden en condensatoren zijn gemaakt van ideale, perfect weerstandsvrije, verliesvrije materialen. Eén van de condensatoren wordt opgeladen tot een potentiaal, V_i, dus de opgeslagen lading is Q = CV_i. Er is geen potentiaalverschil op de andere condensator, dus deze heeft geen opgeslagen lading. Wat gebeurt er als u de schakelaar sluit?

Schema van de twee-condensatorparadox. Eén condensator heeft een potentiaalverschil tussen de platen. Wat gebeurt er als de schakelaar gesloten is?
Sommige presentaties van dit gedachte-experiment gooien er een rode haring tussen en beweren dat de lading van de eerste condensator naar de tweede zal stromen, waardoor het potentiaalverschil op de eerste kleiner wordt en op de tweede groter, totdat een stabiele toestand wordt bereikt – op dat moment is het potentiaalverschil op beide condensatoren gelijk en de helft van V_i, aangezien dezelfde lading, Qwordt nu verdeeld over twee gelijkwaardige condensatoren. Dit leidt echter meteen tot een paradox, want de energie in elke condensator is W_C = \frac{1}{2} C \Delta V^2. Als de aanvankelijke energie \frac{1}{2} C V_i^2 en de uiteindelijke energie is 2 \frac{1}{2} C_left( V_i/2 \right)^2 = \frac{1}{4} C V_i^2waar is de andere helft van de energie gebleven?
Er zijn veel oplossingen beschikbaar die zich beroepen op alles van kwantummechanica tot thermodynamica. Deze oplossingen zijn waarschijnlijk allemaal geldig vanuit educatief oogpunt. Veel van deze oplossingen doen echter een impliciet beroep op de werkelijkheid door te zeggen dat de draden en condensatoren gewoon een bepaalde weerstand of inductantie moeten hebben. Maar waarom? Tenminste binnen de context van een gedachte-experiment kan het redelijk zijn om perfect verliesvrije materialen aan te nemen, en dus de weerstand te verwaarlozen. Maar hoe zit het met de inductantie? Kunnen we binnen de context van dit gedachte-experiment inductantie verwaarlozen? Laten we deze vraag volgen en kijken of het een interessant antwoord oplevert…
Een eenvoudige oplossing voor de paradox
Ons apparaat bestaat uit twee ideale, verliesloze condensatoren. Maar zelfs een ideale condensator moet zijn ladingen ruimtelijk scheiden. Dat wil zeggen, een condensator moet een bepaalde grootte hebben. En als elke condensator afmetingen heeft, dan moet hij op een niet-nul afstand van de andere condensator staan. Dus als we ons diagram een klein beetje hertekenen, zien we dat we twee condensatoren hebben en twee halve lussen van verliesloze draad met een eindige diameter, waarlangs een tijdsafhankelijke stroom kan lopen. Maar hoe noemen we zo’n structuur? Een spoel!
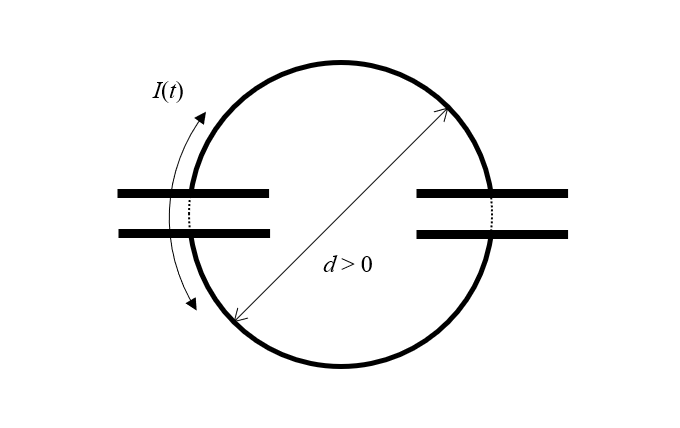
De paradox kan worden opgelost door te beseffen dat de structuur een niet-nulgrootte moet hebben, waarbij de stroom rond een lus van eindige oppervlakte stroomt, en daarom ook een spoel is.
De structuur die we hier getekend hebben moet eindige afmetingen hebben, en dus ook inductantie, zolang het bestaat binnen ons universum, waar de vrije ruimte magnetische permeabiliteit heeft. Dus simpelweg als gevolg van het feit dat er een condensator in ons circuit zit, moet er ook een inductor in het circuit zitten. Eigenlijk wordt het nog beter: Als we een spoel hebben, zelfs een zonder verlies, zal elke tijdsafhankelijke stroom die er doorheen loopt leiden tot een elektrisch veld tussen de windingen van de spoel, en dus werkt elke spoel die we aan deze schakeling toevoegen ook als een condensator! We zouden deze logica oneindig kunnen doortrekken, maar voor ons doel is het voldoende om onze schakeling aan te passen met een enkele spoel die een inductie heeft, L.
We hebben nu een LC circuit, en dit heeft een analytische oplossing die de paradox meteen opheldert: Er zal stroom heen en weer stromen tussen de condensatoren en langs de eindige-lengte draden, oscillerend met een frequentie gegeven door: f=1/elfsqrt{2pi LC}. Er zal nooit een stationaire oplossing zijn, dus we kunnen nooit alleen de elektrostatische energie evalueren. We moeten ook rekening houden met de energie als gevolg van de bewegende ladingen, d.w.z. de stroom, I, en dit wordt gegeven door: W_L = \frac{1}{2} L I^2. De som van deze elektrische en magnetische energie (\frac{1}{2} L I^2 + \frac{1}{2} C V^2) zal in de loop van de tijd niet veranderen.
Verifiëren in COMSOL Multiphysics® Software
Het is eenvoudig om een model te bouwen dat deze situatie verifieert met COMSOL Multiphysics.® en de RF-module. We zullen dit doen met behulp van de Elektromagnetische golven, voorbijgaande interface samen met de Elektrostatica interface om de beginvoorwaarden te berekenen. We zullen een klein gebied van perfect vacuüm modelleren met de condensatoren en draden erin. De condensatorplaten, draden en ruimte rondom ons volume worden allemaal behandeld als perfecte elektrische geleiders, wat betekent dat de elektromagnetische velden door geen enkele grens zullen doordringen. Er is een handleiding voor het opzetten van dergelijke modellen voor capacitieve ontlading in ons artikel in het Leercentrum: “Capacitieve ontlading modelleren”.
Het oplossen van dit tijd-domein model en het evalueren van de totale elektrische en magnetische energie laat het verwachte oscillerende gedrag zien. Het is ook mogelijk om het modelleringsdomein in verschillende gebieden op te delen om de totale energie in de gebieden rond de twee condensatoren en in de omringende ruimte te evalueren. Deze grafiek laat zien hoe de energie zowel in de ruimte als in de tijd oscilleert.
Animatie die de stromen op het oppervlak van de condensatorplaten en -draden toont, evenals het magnetische veld in de ruimte ertussen.
De totale elektrische en magnetische energie schommelen in de tijd; de som verandert niet in dit verliesloze apparaat.
Het totaal van de elektrische en magnetische energie in verschillende domeinen laat zien dat de energie schommelt in tijd en ruimte.
We kunnen waarnemen dat deze grafieken niet zuiver sinusvormig zijn in de tijd, en we moeten ons afvragen waarom dat zo is. Waar komt deze hogere frequentie-inhoud, d.w.z. de rimpelingen in de energie in de tijd, vandaan? Ze komen voort uit de structuur. Het is heel duidelijk dat de twee platen een goed gedefinieerde capaciteit hebben, maar er is ook een ladingsafscheiding door de draden, en deze hele structuur zit in een cilindrische holte die een resonantiefrequentie heeft. Al deze verschillende onderdelen van het apparaat hebben een bepaalde bijdrage aan het elektromagnetische gedrag. Elke bijdrage kan heel klein zijn, maar ze bestaat altijd als we een structuur met eindige afmetingen bekijken.
Meer vragen stellen: Bestaan capaciteit en inductie?
Het is nu tijd om een meer provocerende vraag te stellen over dit (of elk ander) elektromagnetische apparaat: Heeft het een capaciteit of inductantie? We hebben duidelijk gezien dat dit specifieke apparaat beide heeft. Maar wat als we het aanpassen door een zeer sterk diëlektrisch materiaal tussen de condensatorplaten toe te voegen? Dat zou de capaciteit veel groter maken, maar de inductantie onveranderd laten. En als we de capaciteit veel groter maken, kunnen we dan zeggen dat de inductantie er niet toe doet?
Kortom: Nee, we mogen nooit denken dat een elektrodynamisch apparaat puur capacitief of puur inductief is. In een elektrodynamisch apparaat zal er altijd elektrische energie zijn als gevolg van ruimtelijke scheiding van ladingen en magnetische energie als gevolg van beweging van ladingen. Hoewel we soms hypothetische situaties kunnen bedenken waarin het een of het ander genegeerd kan worden, moeten we altijd onthouden dat we een mentale vereenvoudiging maken.
Bovendien hebben alle echte materialen ook een bepaalde eindige weerstand, dus om realistischer te zijn, moeten we over alles spreken als hebbende een impedantie – en dit is waar we onszelf soms in nog meer problemen brengen. Wanneer we te maken hebben met een frequentiedomeinmodel, bestaat er een zeer bekende uitdrukking voor de impedantie van een elektrisch apparaat:
Z = R + j\frac{1}{\omega L -j\frac{1}{\omega C}}.
De weerstand, Rin deze uitdrukking is een maat voor de manier waarop de kinetische energie van de bewegende ladingen, d.w.z. de stroom, wordt omgezet in thermische energie.
Deze vergelijking is onmiddellijk herkenbaar als betrekking hebbend op een gedempte harmonische oscillator met één graad van vrijheid, een van de meest bestudeerde problemen in de techniek en natuurkunde. We weten dat we uit deze uitdrukking de resonantiefrequentie en kwaliteitsfactor van zo’n oscillator kunnen berekenen, en we weten dat echte apparaten een fundamentele resonantie en kwaliteitsfactor hebben. Dit brengt ons in de verleiding om de twee gelijk te stellen en te proberen om een echt elektrisch apparaat met eindige afmetingen te reduceren tot een enkele weerstand, capaciteit en inductie. Dit is een conceptuele fout en is nooit geldig omdat de bovenstaande uitdrukking voor impedantie alleen van toepassing is op een apparaat met oneindig kleine afmetingen.
Elk echt apparaat heeft eindige afmetingen, en wanneer het in resonantie werkt, variëren de elektrische en magnetische energie in ruimte en tijd, zoals we in de bovenstaande diagrammen zagen. Daarom zijn er voor een model van een equivalente schakeling minstens drie knooppunten nodig, hoewel het er soms veel meer kunnen zijn. Als we onze gedachten terugbrengen naar ons fysieke model van de twee condensatoren en aannemen dat de plaat van elke condensator wordt voorgesteld door een knooppunt in het elektrische circuit, zien we dat het equivalente circuitmodel minstens zo ingewikkeld zou moeten zijn als het circuit dat hieronder is afgebeeld, met vier knooppunten. Merk op dat er parallel aan de inductantie van de draden een kleine capaciteit is toegevoegd, aangezien er ook een scheiding van lading langs de draden is.
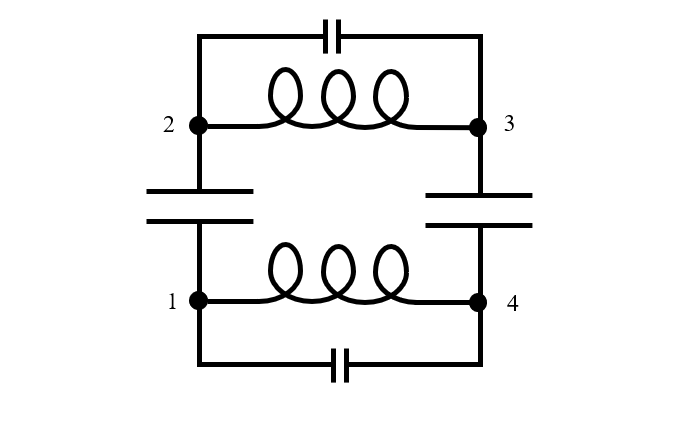
Een equivalent circuitmodel van twee in serie geschakelde verliesloze condensatoren van eindige grootte.
Hopelijk kunnen we aan de hand van dit voorbeeld zien dat het construeren van een equivalent circuitmodel dat geldig is in de buurt van resonantie al snel erg ingewikkeld kan worden, waarbij natuurkundig inzicht, een flinke dosis ervaring met soortgelijke apparaten en numerieke modellering nodig zijn.
Om terug te keren naar de oorspronkelijke vraag, zou men kunnen stellen dat capaciteit, inductie en zelfs weerstand concepten zijn die niet op zichzelf bestaan – dat ze alleen in combinatie met elkaar bestaan. Hoewel we de frequentie-afhankelijke impedantie van een apparaat soms kunnen herleiden tot een enkele weerstand, capaciteit en/of inductantie, zijn dergelijke vereenvoudigingen alleen geldig bij frequenties onder de resonantie van het apparaat. Als we dit in gedachten houden, kunnen we allerlei valkuilen vermijden, variërend van deze vermakelijke twee-condensatorparadox tot veel frustrerendere, complexe problemen in de echte wereld.
Slotopmerkingen
We hebben hier een klassiek gedachte-experiment gebruikt om te begrijpen waarom de impedantie van een elektromagnetisch apparaat dat in de buurt van resonantie werkt, niet kan worden ontleed in een enkele equivalente weerstand, capaciteit en inductantie. Gedachte-experimenten zoals de twee-condensatorparadox zijn waardevol voor het verbreden van ons begrip van elektromagnetica en het interpreteren van de resultaten van onze rekenmodellen.
Verder lezen
Wilt u weten hoe modellering en simulatie kunnen worden gebruikt om andere hersenkrakers op te lossen? Bekijk enkele andere voorbeelden op de COMSOL Blog:
Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.


