Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.
Istnieje wiele sytuacji, w których mogą być Państwo zainteresowani modelowaniem okresowych, choć niesinusoidalnych, sygnałów elektrycznych w celu obliczenia wynikowych pól elektrycznych, strat termicznych i zmian temperatury. Jednym z przykładów może być zastosowanie ciągów impulsów elektrycznych do tkanek ludzkich w celu neuromodulacji, elektroporacji lub ablacji termicznej. Chociaż takie sygnały można symulować za pomocą modelowania w dziedzinie czasu, możliwe jest również wydajne obliczenie odpowiedzi liniowej za pomocą transformaty Fouriera. Proszę dowiedzieć się więcej!
Spis treści
- Wprowadzenie
- Zrozumienie zawartości częstotliwościowej sygnału wejściowego
- Rozwiązywanie w dziedzinie częstotliwości
- Rekonstrukcja wyników przejściowych
- Wykorzystanie wyników FFT do analizy termicznej
- Zmiana typu impulsu i odstępu między impulsami
- Ignorowanie efektów pojemnościowych dla dalszego uproszczenia
- Uwagi końcowe
Wprowadzenie
Będziemy kontynuować pracę z przykładowym modelem, którego używaliśmy w naszym poprzednim wpisie na blogu „Understanding the Transient Electromagnetic Excitation Options” i rozwiążemy go za pomocą funkcji Prądy elektryczne interfejs. (Interfejs ten został wyróżniony w naszym poprzednim wpisie na blogu i wykazano, że jest wystarczający do rozwiązania tego typu modelu). Wzbudzenie prądowe jest trapezoidalnym przebiegiem impulsowym o okresie 1 µs. Model ten można rozwiązać w dziedzinie czasu. Poniżej przedstawiono napięcie na zaciskach i całkowite straty w modelu.
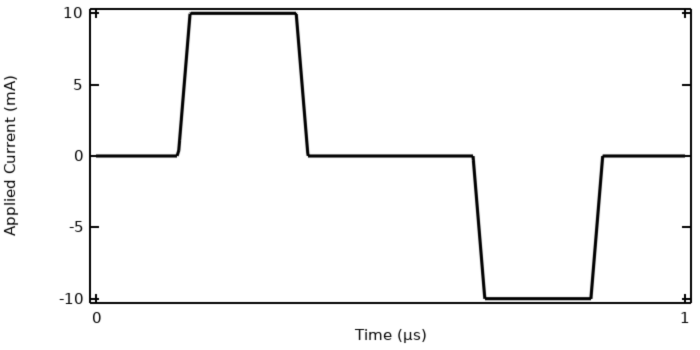
Prąd przyłożony do modelu, ramped trapezoidalna fala impulsowa.
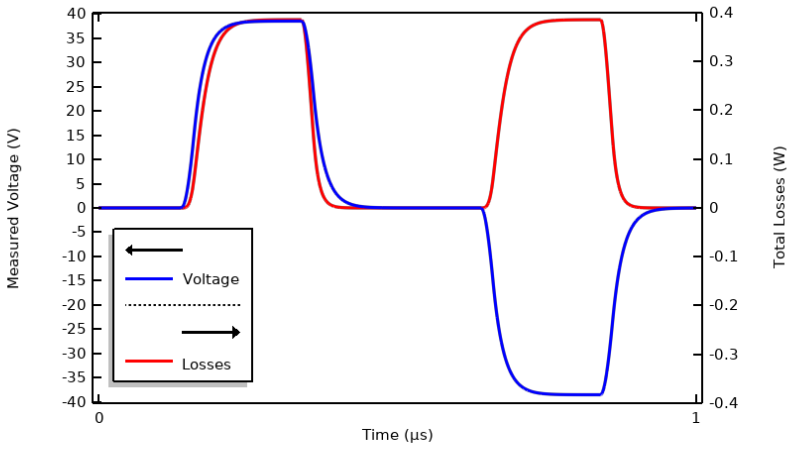
Obliczone napięcie na zaciskach i straty w materiale w jednym okresie.
Możemy również rozszerzyć model, aby rozwiązać go dla temperatury i uczynić przewodność elektryczną funkcją temperatury, przekształcając go tym samym w dwukierunkowo sprzężony model wielofizyczny. Wyrażenie, którego użyjemy to \sigma (T) = 0.03\exp \left(-\frac{T-20^\circ \text{C}}{20\text{K}}\right) \text{S/m}..
Stały warunek brzegowy temperatury jest stosowany wzdłuż boku i dna domeny modelowania. Model jest rozwiązywany dla pojedynczego okresu czasu (1 µs), a zmiany temperatury w tym okresie można zbadać. Jak widać na poniższym obrazku, zmiana temperatury jest minimalna.
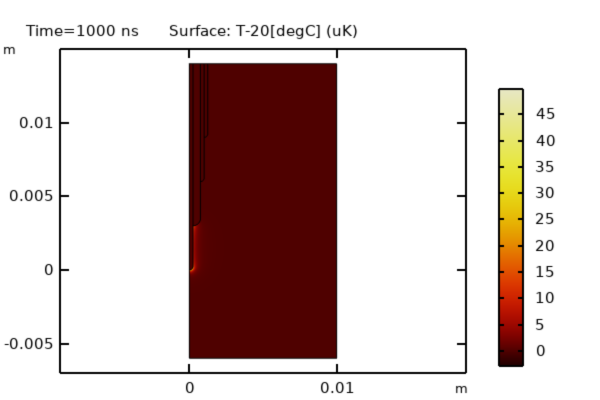
Obliczona zmiana temperatury po 1 mikrosekundzie jest niewielka.
Będziemy jednak chcieli rozwiązać problem zmian temperatury w znacznie dłuższych przedziałach czasowych niż jeden okres, a do tego to podejście do modelowania będzie zbyt kosztowne obliczeniowo. Będziemy musieli poszukać innych podejść. Zanim jednak do tego przejdziemy, należy poczynić kilka uwag na temat tego modelu i wyników:
- Przyłożony prąd zmienia się wokół uśrednionej wartości zerowej, więc sygnał wejściowy nie ma składowej stałej.
- Obliczone napięcie na zaciskach i straty spadają do zera pomiędzy impulsami.
- Ani przewodność elektryczna, ani względna przenikalność elektryczna nie zależą bezpośrednio od pola elektrycznego.
- Napięcie końcowe opóźnia prąd, co oznacza, że układ ma znaczną pojemność.
- Wzrost temperatury w jednym okresie wzbudzenia jest bardzo mały.
W konsekwencji obserwacji, że wzrost temperatury jest bardzo mały w okresie podobnym do okresu wzbudzenia elektrycznego, możemy traktować problem elektryczny jako lokalnie liniowy w czasie. Pozwala nam to na odtworzenie wyników poprzez transformatę Fouriera zastosowanego sygnału, a następnie rozwiązanie modelu w dziedzinie częstotliwości i zastosowanie odwrotnej transformaty Fouriera do odtworzenia wyników przejściowych dla modelu elektrycznego. W ten sposób szybko uzyskujemy informacje o tym, które harmoniczne sygnału wejściowego znacząco przyczyniają się do nagrzewania.
Rozwiązywanie przejściowych zmian temperatury w czasie znacznie dłuższym niż okres wzbudzenia można osiągnąć za pomocą dwukierunkowo sprzężonego modelu, który rozwiązuje pole temperatury wraz z kilkoma harmonicznymi. Prądy elektryczne interfejsów, po jednym dla każdej znaczącej składowej częstotliwości sygnału wejściowego. Będzie to znacznie bardziej wydajne obliczeniowo. Istnieje kilka kroków tego podejścia do modelowania, jak opisano w naszych artykułach Centrum Nauki „Zrozumienie sygnałów okresowych i ich zawartości częstotliwościowej”, „Wykorzystanie odwrotnej szybkiej transformaty Fouriera do rekonstrukcji sygnału przejściowego” oraz „Konfigurowanie i rozwiązywanie problemów z ogrzewaniem elektromagnetycznym”. Podsumujemy te kroki tutaj.
Zrozumienie zawartości częstotliwości sygnału wejściowego
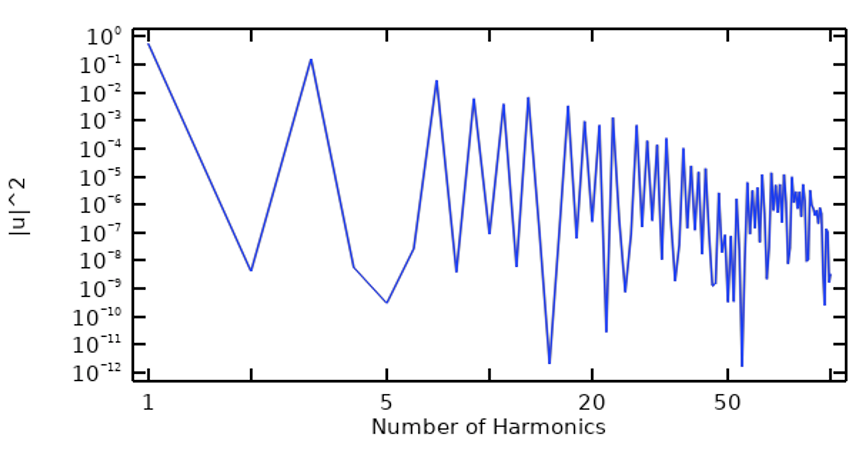
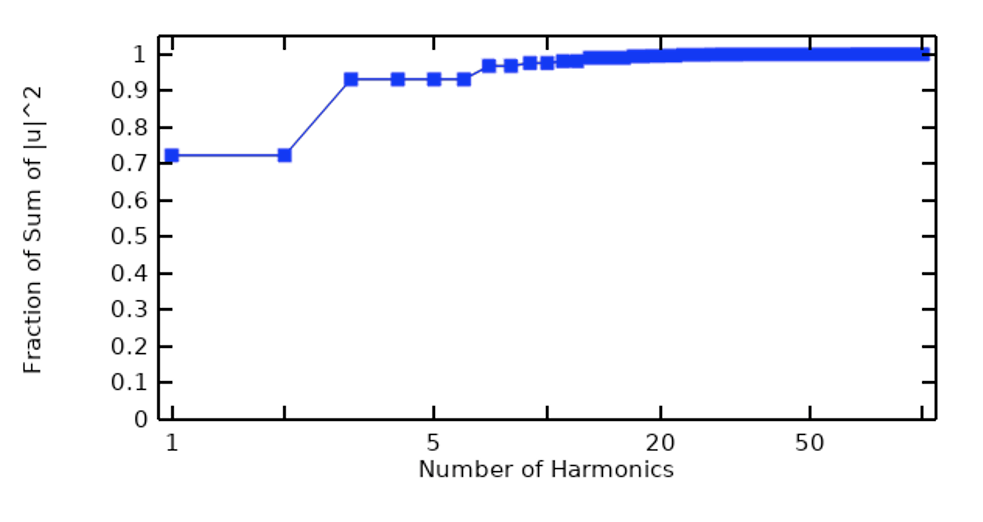
Zaczynając od sygnału okresowego, możemy wykonać szybką transformatę Fouriera (FFT) sygnału, aby zbadać jego zawartość częstotliwościową, co można zrobić pod względem wielkości każdej harmonicznej, a także pod względem skumulowanej sumy do bieżącej harmonicznej. Na poniższych rysunkach obraz po lewej stronie to wykres zawartości częstotliwości trapezoidalnej fali impulsowej, a obraz po prawej to skumulowana suma.
Zawartość częstotliwościowa trapezoidalnej fali impulsowej (po lewej) i pod względem sumy skumulowanej (po prawej).
Na tym wstępnym etapie możemy zauważyć, że przynajmniej w tym przykładzie tylko stosunkowo niewielka liczba harmonicznych wnosi większość energii w sygnale, a niektóre harmoniczne mają znikomy wkład.
Rozwiązywanie w dziedzinie częstotliwości
Wraz z FFT przyłożonego sygnału, musimy również obliczyć odpowiedź układu na wzbudzenie w dziedzinie częstotliwości, ze wzbudzeniem o tej samej wielkości na wszystkich częstotliwościach. Proszę zauważyć, że nie oznacza to, że odpowiedź układu będzie równoważna na wszystkich częstotliwościach – temat ten został szczegółowo omówiony w naszym wpisie na blogu „Zrozumienie opcji wzbudzenia do modelowania prądów elektrycznych”. Wyniki zamiatania w zakresie częstotliwości pokazano poniżej na wykresie uśrednionych strat cyklicznych, z którego możemy wywnioskować, że model, z którym pracujemy, ma impedancję, która zmienia się znacząco wraz z częstotliwością. W tym przypadku rozwiążemy dla pierwszych 100 harmonicznych, a gdy będziemy wiedzieć, które częstotliwości są ważne, możemy uruchomić mniejszy zestaw częstotliwości.
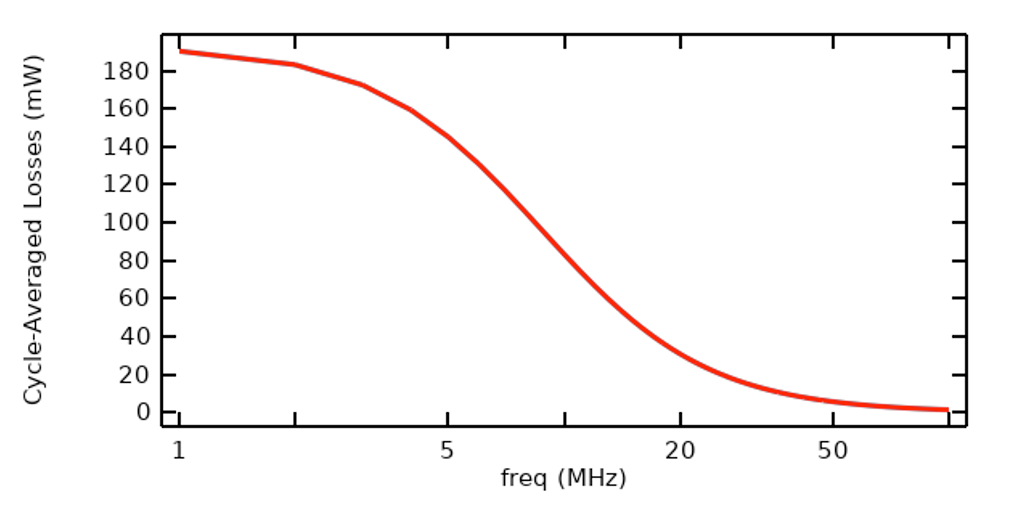
Wykres uśrednionych strat w próbce w funkcji częstotliwości, z równoważnym wzbudzeniem przy wszystkich częstotliwościach.
Rekonstrukcja wyników przejściowych
Ponieważ mamy już FFT sygnału wejściowego, po obliczeniu wyników w dziedzinie częstotliwości, z jednostkowym wzbudzeniem na wszystkich rozważanych częstotliwościach, możemy użyć odwrotnej szybkiej transformaty Fouriera (IFFT) do odtworzenia odpowiedzi przejściowej systemu. Poniższy wykres pokazuje doskonałą zgodność, a podejście IFFT jest mniej intensywne obliczeniowo.
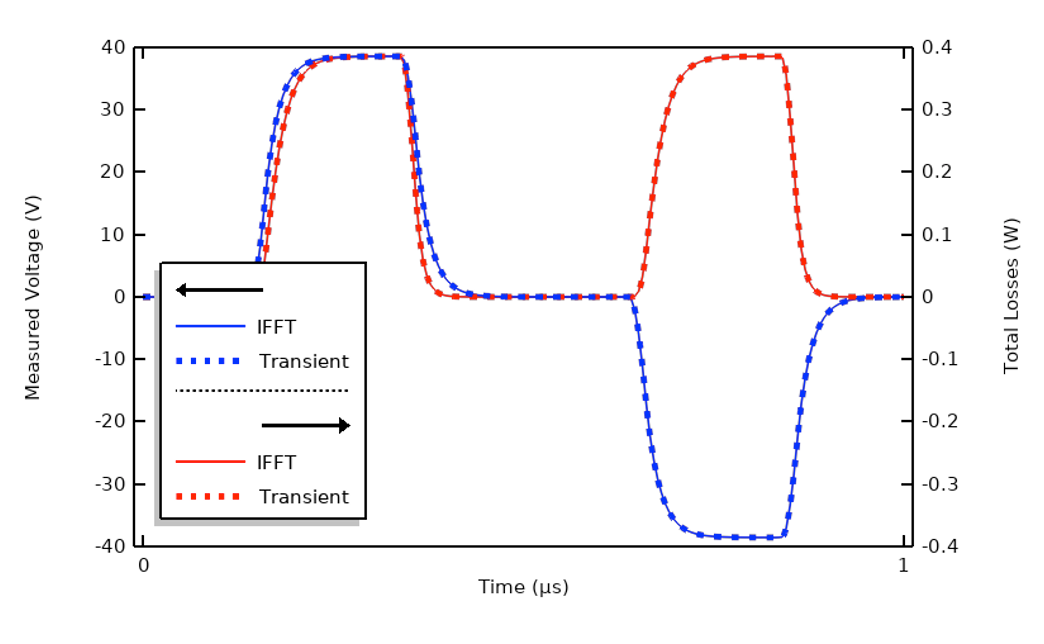
Porównanie wyników przejściowych i wyników rekonstrukcji za pomocą IFFT przy użyciu 100 harmonicznych.
Chociaż uzyskanie doskonałej zgodności w zakresie wyników przejściowych może być przydatne, często interesuje nas tylko ogrzewanie, więc zamiast oceniać wyniki IFFT pod względem ich zgodności w dziedzinie czasu, przydatne jest również porównanie strat zintegrowanych w czasie w jednym cyklu. Dla tego zastosowanego sygnału 99% strat jest wychwytywanych przez rozwiązanie tylko dla pierwszej, trzeciej, siódmej i dziewiątej harmonicznej. Oznacza to, że całkowite zintegrowane straty zgadzają się całkiem dobrze, mimo że wyniki przejściowe są zauważalnie różne.
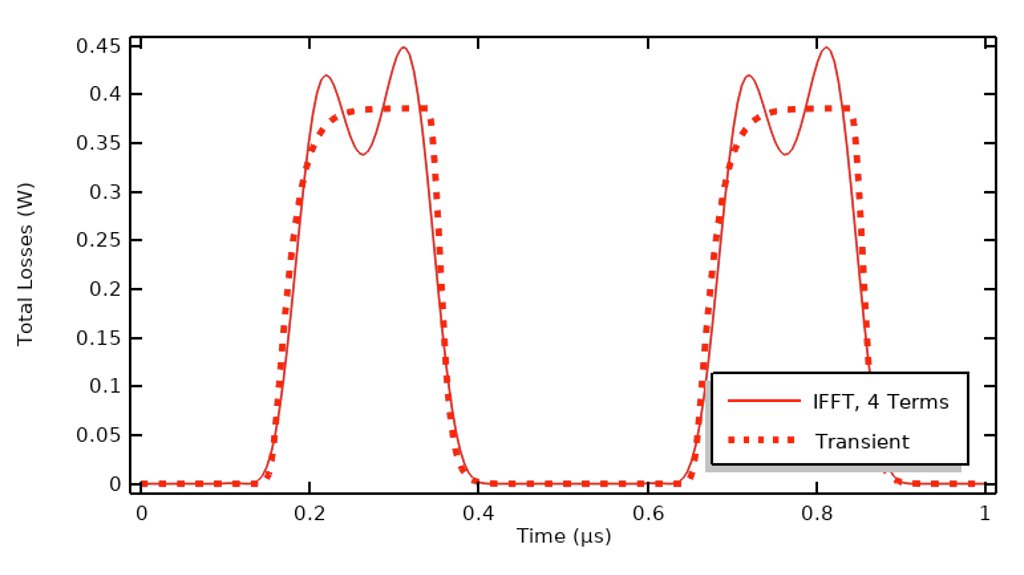
Porównanie strat w dziedzinie czasu i strat zrekonstruowanych za pomocą IFFT przy użyciu tylko czterech harmonicznych.
Na powyższym rysunku widzimy, że chociaż zgodność nie wygląda tak dobrze, całka strat w całym okresie czasu zgadza się w granicach 1%.
Wykorzystanie wyników FFT do analizy termicznej
Do tej pory przyjrzeliśmy się, jak zrekonstruować zmienność strat przejściowych w jednym okresie, ale do celów analizy termicznej prawdopodobnie będziemy zainteresowani modelowaniem znacznie dłuższych czasów, ponieważ zmiany temperatury występują w przedziałach czasowych wielokrotnie dłuższych niż okres sygnałów elektrycznych. Jeśli mamy materiały, w których przewodnictwo elektryczne zmienia się wraz z temperaturą, będziemy chcieli uwzględnić to dwukierunkowe sprzężenie między fizyką w naszym modelu. Gdybyśmy próbowali rozwiązać jednocześnie pola elektryczne i pola temperatury, z wystarczająco dokładną rozdzielczością czasową, aby uchwycić wzbudzenie elektryczne, wówczas otrzymalibyśmy model, którego rozwiązanie zajęłoby bardzo dużo czasu. Chociaż czasami jest to uzasadnione, często chcemy szybszego podejścia i właśnie w tym przypadku dane, które obliczyliśmy do tej pory, staną się bardzo przydatne.
Jak pokazano poniżej, straty w dziedzinie czasu można przybliżyć jako równomierne w czasie, w oparciu o sumę wkładów z kilku pierwszych harmonicznych. Jest to słuszne przy założeniu, że termiczna skala czasowa jest znacznie dłuższa niż okres elektryczny.
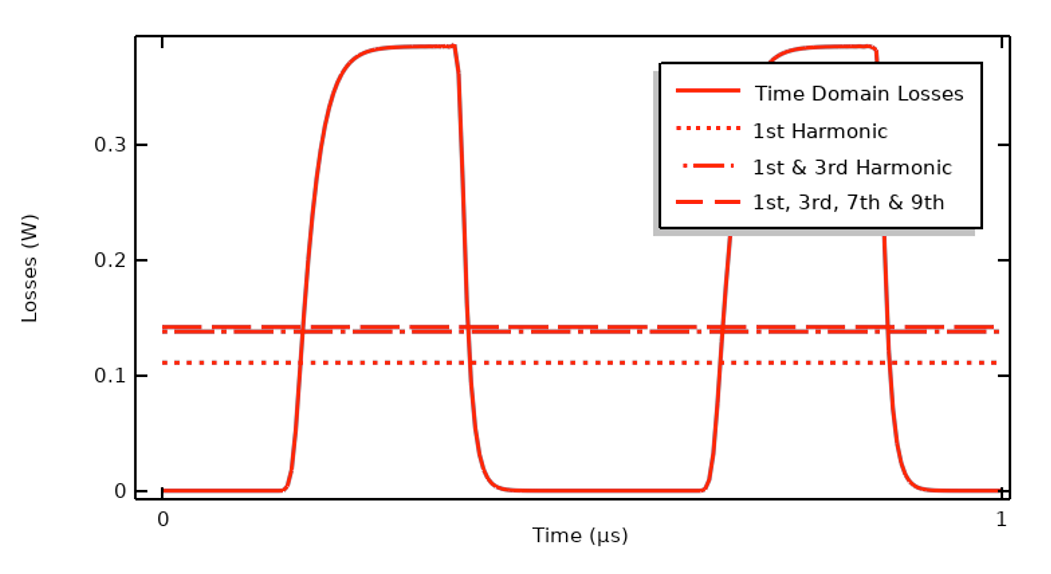
Wykres porównujący straty w dziedzinie czasu i sumę średniej cyklicznej obliczonej dla kilku harmonicznych.
Jak zauważyliśmy wcześniej, dla tego sygnału wejściowego potrzebujemy tylko podstawowej, trzeciej, siódmej i dziewiątej harmonicznej, aby uchwycić 99% ogrzewania w jednym okresie. Oznacza to, że możemy skonfigurować nowy model z czterema różnymi harmonicznymi. Prądy elektryczne W tym celu należy utworzyć interfejsy fizyczne, z których każdy jest rozwiązywany w dziedzinie częstotliwości dla innej harmonicznej, i pomnożyć wielkość przyłożonego prądu dla każdej harmonicznej przez odpowiedni współczynnik Fouriera sygnału wejściowego. Interfejsy te można następnie rozwiązać wraz z przejściowym (lub stacjonarnym) modelem termicznym, który obliczy zmiany temperatury i uwzględni dwukierunkowe sprzężenie, które powstaje, ponieważ właściwości materiału elektrycznego są funkcjami temperatury. Takie podejście jest stosunkowo bardziej wydajne obliczeniowo i pozwala na modelowanie geometrii 3D. Aby uzyskać wskazówki dotyczące konfigurowania takich modeli, w których wyniki FFT sygnału wejściowego są wykorzystywane do definiowania obciążeń cieplnych, proszę zapoznać się z naszym artykułem „Konfigurowanie i rozwiązywanie problemów z ogrzewaniem elektromagnetycznym”.
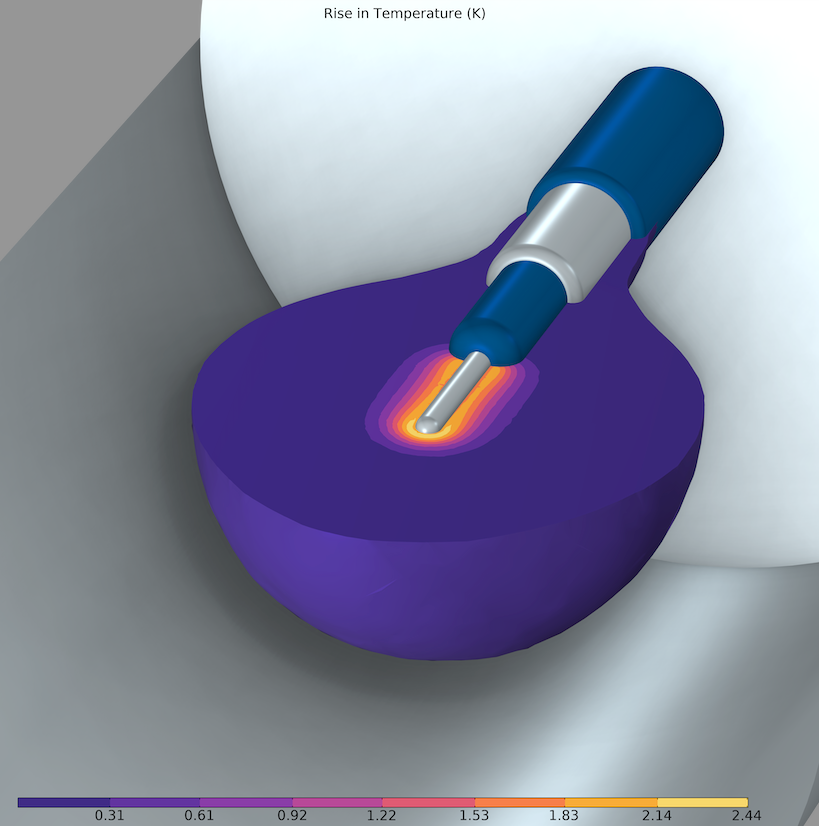
Wzrost temperatury obliczony w modelu 3D przy użyciu uśrednionego cyklicznie nagrzewania spowodowanego sumą harmonicznych zastosowanego przebiegu prądu.
Zmiana typu impulsu i odstępów między impulsami
Warto również zastanowić się, co się stanie, jeśli będziemy chcieli modelować ciąg impulsów, sygnał, który jest ściśle dodatni. Sygnał ten ma składową stałoprądową, co teoretycznie sprawia, że IFFT jest bardziej zaangażowany, ponieważ musimy również wziąć pod uwagę rozwiązanie stacjonarne. Ale ponieważ interesuje nas tylko ogrzewanie i jeśli straty spadają do zera między impulsami, to znak wzbudzenia nie ma znaczenia. Oznacza to, że nagrzewanie elektryczne jest takie samo niezależnie od kierunku przepływu prądu. Jeśli nagrzewanie w czasie spada do zera między impulsami, wówczas nie ma składowej stałej nagrzewania, którą należy uwzględnić w IFFT. Tak więc, nawet gdy mamy do czynienia z sygnałem wejściowym, który jest ściśle dodatni, rozsądne może być traktowanie go jako sygnału, który przełącza się z dodatniego na ujemny, wyłącznie w celu uproszczenia rekonstrukcji IFFT. Poniższy sygnał i wcześniej przedstawiony sygnał są identyczne pod względem obliczonych strat.
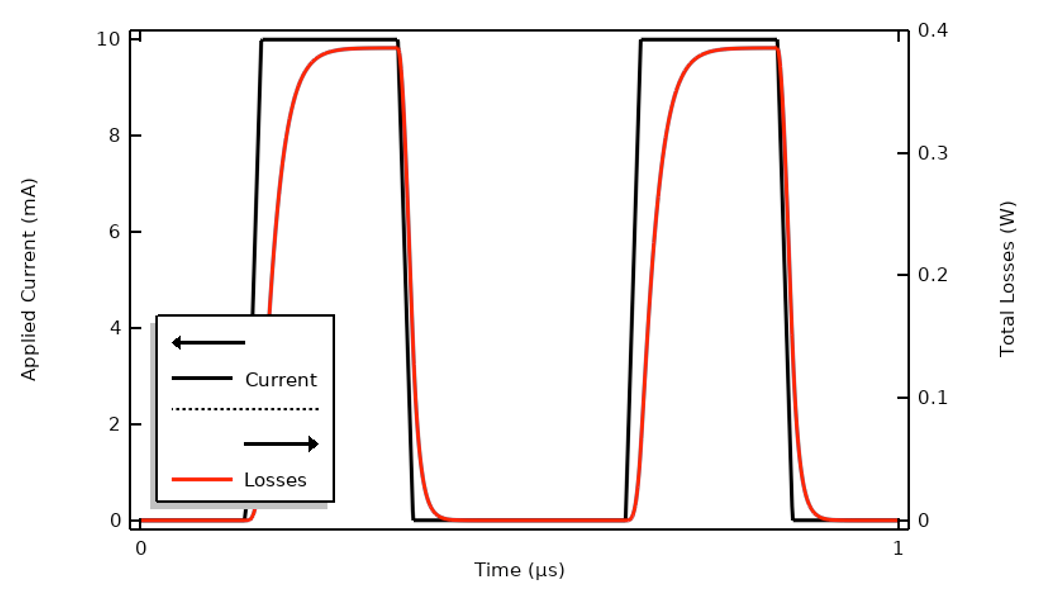
Sygnał wejściowy, który jest ściśle dodatni, będzie miał identyczne ogrzewanie w porównaniu z sygnałem symetrycznym, o ile profil ogrzewania osiągnie zero pomiędzy nimi.
Zmieńmy również odstępy między impulsami. Zwiększa to okres sygnału wejściowego, więc możemy pomyśleć, że musimy powtórzyć FFT. Ponieważ jednak ogrzewanie spada do zera między impulsami w naszym oryginalnym sygnale, dodanie dłuższego czasu, w którym ogrzewanie jest zerowe, nie zmienia strat spowodowanych pojedynczym impulsem. Oznacza to, że jeśli mamy ciąg impulsów z długim okresem między impulsami, wystarczy wykonać FFT sygnału z krótszym czasem między impulsami, ponieważ jest to wystarczające do dokładnego przewidzenia profilu ogrzewania i oszczędza trochę wysiłku obliczeniowego. Podczas rozwiązywania dwukierunkowo sprzężonego problemu termicznego, zastosowany sygnał musi zostać przeskalowany w dół o współczynnik pierwiastka kwadratowego z cyklu pracy. Na poniższym rysunku impulsy mają równoważny czas trwania, ale okres jest podwojony, więc cykl pracy wynosi 0,5.

Zwiększenie czasu między impulsami nie zmienia profilu nagrzewania każdego impulsu.
Ignorowanie efektów pojemnościowych dla dalszego uproszczenia
Przykład, który rozważaliśmy do tej pory, został zaprojektowany (pod względem właściwości materiałów i kształtu fali) w celu zilustrowania przypadku, w którym podejście FFT jest najbardziej przydatne. Ten poziom złożoności nie zawsze jest potrzebny. Wróćmy do naszego pierwszego wykresu przyłożonego prądu i napięcia końcowego i odtwórzmy go z innym materiałem próbki, takim o przewodności elektrycznej, która jest dziesięć razy większa. Spowoduje to odpowiedź podobną do poniższego rysunku. Opóźnienie między napięciem i prądem w stosunku do okresu jest znikome, co oznacza, że prawie nie występują efekty pojemnościowe. Lub: Impedancja systemu jest prawie czysto rezystancyjna i stała w interesującym nas zakresie częstotliwości. Podobnie, gdyby zastosowano ten sam kształt fali, ale dziesięciokrotnie wolniejszy, odpowiedź wyglądałaby podobnie.
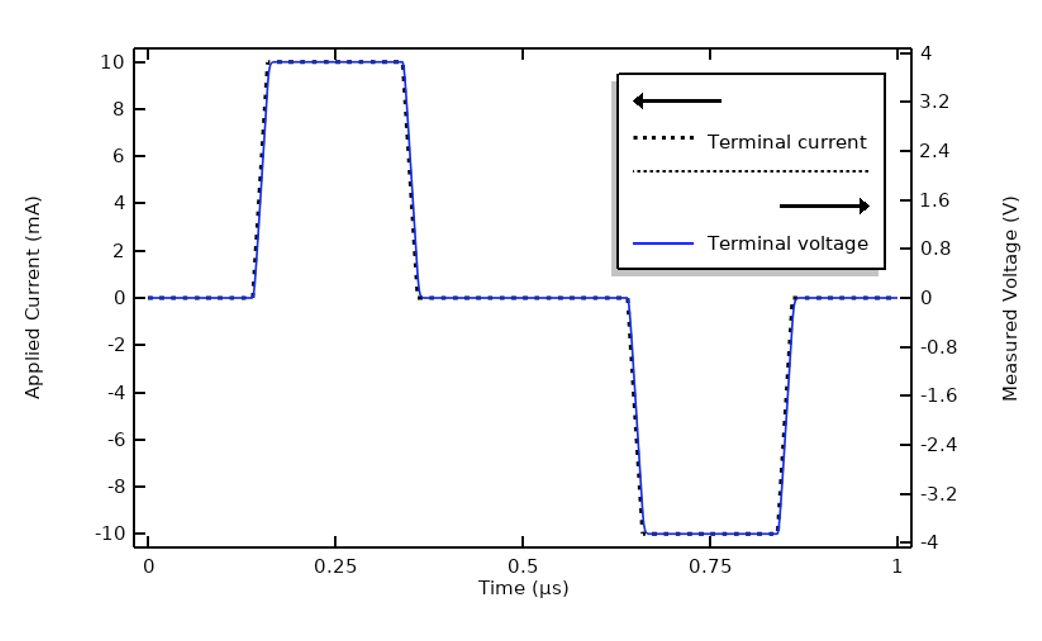
Zmiana przewodności elektrycznej na dziesięciokrotnie większą spowoduje zmianę odpowiedzi systemu. Efekty pojemnościowe są teraz pomijalne.
Zakładając, że mamy do czynienia z układem prawie czysto rezystancyjnym i przy założeniu, że przewodność elektryczna jest stała w odniesieniu do zawartości częstotliwości przyłożonego sygnału, możliwe jest uproszczenie modelu elektrycznego do stacjonarnego problemu prądu stałego, a tym samym całkowite zignorowanie efektów pojemnościowych i wynikających z nich prądów przemieszczenia. The Prądy elektryczne interfejs fizyki można następnie rozwiązać w Stacjonarny a zastosowany sygnał DC jest pierwiastkiem kwadratowym ze średniej cyklu kwadratu sygnału przejściowego:
f_{DC}=\sqrt{\frac{1}{T_1}\int_0^{T_1}f
Wyrażenie to jest takie samo niezależnie od tego, czy wzbudzenie jest wyrażone prądem, napięciem czy napięciem zakończonym. Korzystanie z tego uproszczenia jest uzasadnione, o ile właściwości elektryczne są stałe w odniesieniu do częstotliwości i natężenia pola elektrycznego.
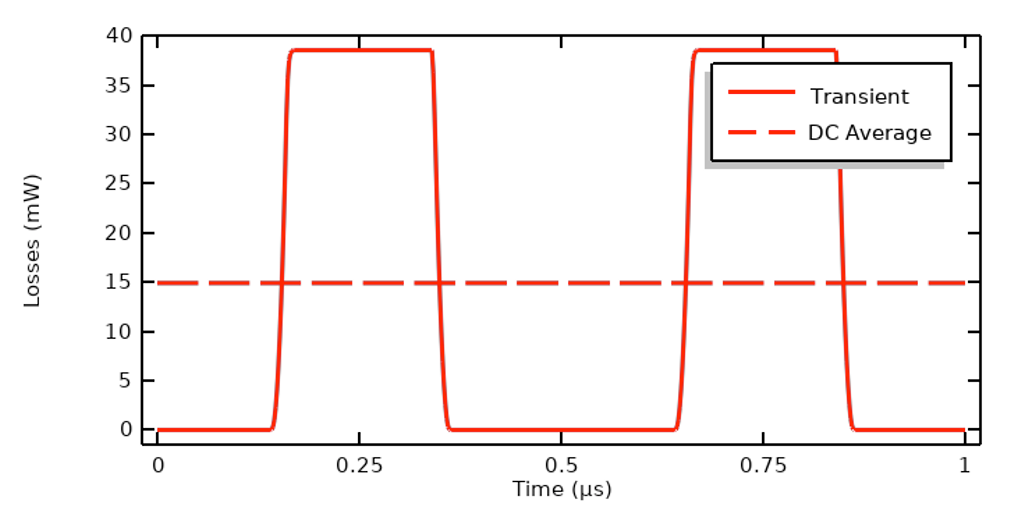
Straty w dziedzinie czasu dla prawie czysto rezystancyjnego materiału i średnia równoważna DC.
Przyjrzeliśmy się, jak modelować wzbudzenie elektryczne, które jest okresowe i jak często można to zredukować do rozważenia pojedynczego okresu. Wykonując FFT sygnału wejściowego, można zidentyfikować ważną zawartość częstotliwości, a odpowiedź układu przejściowego można przewidzieć za pomocą kombinacji rozwiązania dla zestawu częstotliwości i kroku badania IFFT.
Wyniki FFT i IFFT można wykorzystać do przewidywania odpowiedzi w czasie i można je wykorzystać jako dane wejściowe do symulacji ogrzewania elektrotermicznego. Szczególnie efektywne może być aproksymowanie sygnału okresowego jako sumy kilku harmonicznych, co pozwala nam traktować to jako dwukierunkowo sprzężony problem wielofizyczny w bardzo efektywny sposób. W przypadku niektórych typów problemów, możemy dokonać dalszego uproszczenia poprzez całkowite zignorowanie zawartości częstotliwości.
Jeśli zajmują się Państwo modelowaniem w tej dziedzinie, powinni być Państwo w pełni świadomi wszystkich tych zawiłości i uproszczeń podczas tworzenia modeli wielofizycznych.
Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.