Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.
Wraz z wydaniem wersji 6.2 oprogramowania COMSOL Multiphysics® oprogramowanie, możliwości modelowania dyspersji elektrycznej można teraz rozszerzyć na Prądy elektryczne który obsługuje zarówno modelowanie w dziedzinie czasu, jak i częstotliwości. Ta funkcjonalność jest szczególnie ważna dla dokładnego modelowania szerokiej klasy materiałów, w tym izolatorów i żywych tkanek. Przyjrzyjmy się pokrótce, czym jest dyspersja, a następnie pokażemy, jak uwzględnić ją w modelach COMSOL i omówimy, dlaczego jest ważna.
Wprowadzenie
W każdym przypadku modelowania szybkich impulsów prądu elektrycznego stosowanych do żywej tkanki, na przykład w kontekście ablacji serca, elektroporacji lub stymulacji nerwowej, należy wziąć pod uwagę dyspersyjny charakter tkanki, a także izolatory elektryczne.
Wszystkie materiały są elektrycznie dyspersyjne, co oznacza, że względna przenikalność elektryczna zmienia się wraz z częstotliwością wzbudzenia. Przenikalność jest miarą tego, jak materiał zareaguje lub spolaryzuje się w obecności pola elektrycznego. Wielkość tej reakcji zmienia się wraz z częstotliwością ze względu na różne atomy i cząsteczki w materiale oraz ich strukturę. Jest to również miara ilości energii elektrycznej przekształcanej w ciepło lub traconej, gdy materiał jest wystawiony na działanie zmiennego w czasie sygnału. Straty te wynikają ze względnego ruchu atomów i cząsteczek, które oscylują w zmiennych w czasie polach. Podczas pracy w dziedzinie częstotliwości względna przenikalność elektryczna jest wyrażana jako liczba zespolona: \epsilon_r = \epsilon_r^{’} – i \epsilon_r^{„}, gdzie składowe rzeczywista i urojona są powiązane za pomocą wzoru Relacje Kramersa-Kroniga. Na poniższym rysunku przedstawiono dwie takie krzywe dyspersji, reprezentujące odpowiednio materiał izolacyjny i żywą tkankę. Pierwsza z nich ma stosunkowo prostą krzywą, o prawie jednolitych właściwościach w szerokim paśmie częstotliwości, więc widzimy, że nie zawsze konieczne jest rozważanie dyspersji. Z drugiej strony, zawsze istnieje pasmo częstotliwości, w którym występują znaczne różnice we właściwościach i konieczne jest uwzględnienie dyspersji.
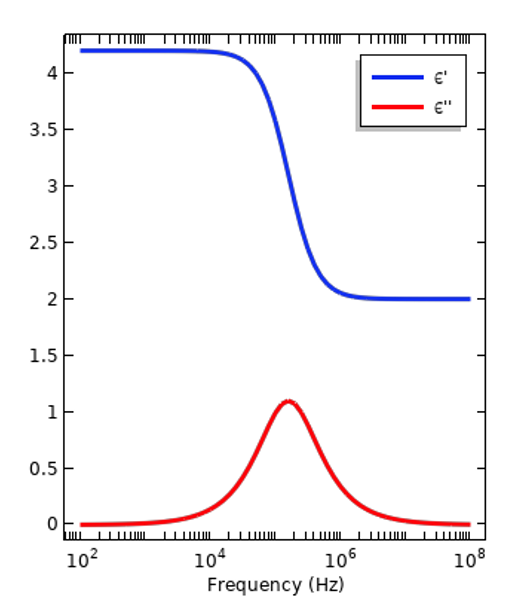
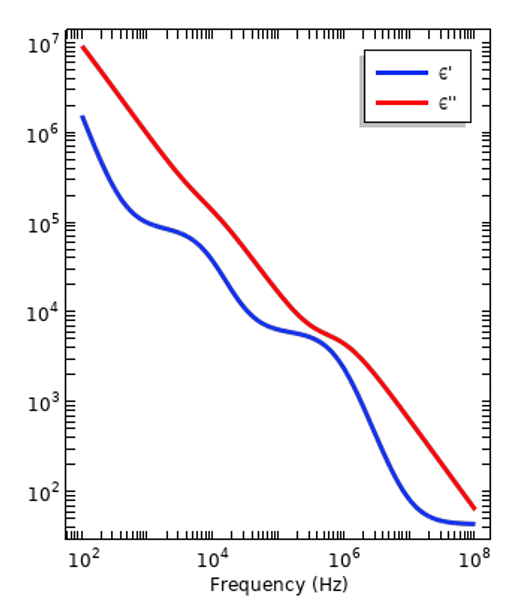
Reprezentatywne krzywe dyspersji izolatora (po lewej) i tkanki ludzkiej (po prawej). Wykreślono wielkość składowej względnej przenikalności elektrycznej o wartości rzeczywistej i urojonej.
Oprócz strat zależnych od częstotliwości występują również straty elektryczne w statycznym polu elektrycznym, które są określane ilościowo przez przewodność elektryczną prądu stałego, \sigma_{DC}. Wszystkie materiały mają pewną przewodność stałoprądową, ale może ona być bardzo, bardzo mała. Jest to oddzielny mechanizm strat od strat dyspersyjnych. Wygodne może być wyrażenie wszystkich strat materiałowych, niezależnie od mechanizmu, poprzez całkowitą przewodność: \sigma_{tot} =\sigma_{DC} + 2\pi f \epsilon_0\epsilon_r^{„}poniżej dla tych samych dwóch materiałów. Należy jednak zauważyć, że przewodność zależna od częstotliwości może być również przedstawiona bez składowej DC jako \sigma(f) = 2\pi f \epsilon_0\epsilon_r^{„} z \sigma_{DC} zgłaszane oddzielnie.
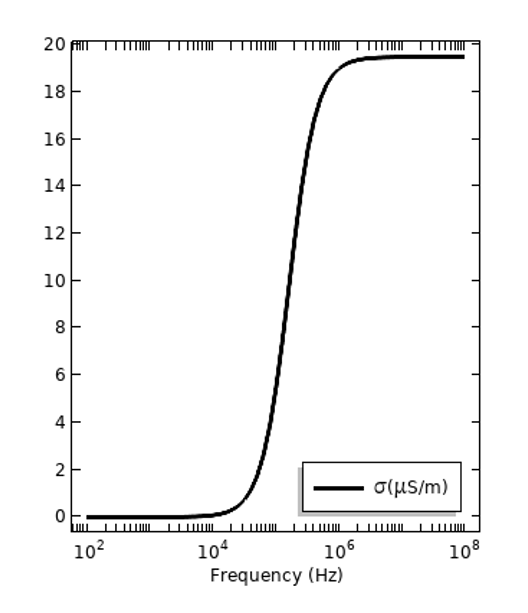
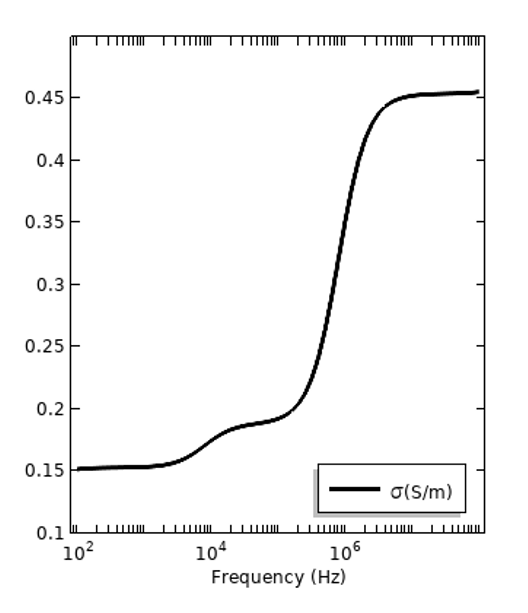
Straty tych samych dwóch materiałów pod względem całkowitej przewodności elektrycznej, z przewodnością stałoprądową przedstawioną jako udział w stratach dyspersyjnych.
Chociaż właściwości materiału są określane eksperymentalnie, nie chcemy bezpośrednio wykorzystywać danych eksperymentalnych, ponieważ będą one obarczone pewną niepewnością i nie będą spełniać relacji Kramersa-Kroniga, prowadząc w ten sposób do modelu nieprzyczynowego. Zamiast tego dopasowujemy do danych funkcję, która już spełnia relacje Kramersa-Kroniga i używamy współczynników tej dopasowanej funkcji do opisania zachowania naszego materiału. Obecnie oprogramowanie obsługuje model Multipole Debye model, który przyjmuje jako dane wejściowe dowolną liczbę, Nbiegunów, gdzie każdy biegun m, ma czas relaksacji, \tau_mi względnej przenikalności elektrycznej, \Delta \epsilon_r_mi na tej podstawie definiuje przenikalność zespoloną jako:
\epsilon_r = \epsilon_\infty + \displaystyle {\sum_{m=1}^N}\frac{\Delta \epsilon_{rm}}{1+i\omega \tau_m}
gdzie \epsilon_\infty opiera się na limicie niskiej częstotliwości, \epsilon_\infty \rightarrow \epsilon_{rS}-\Sigma \Delta \epsilon_r_mlub limit wysokiej częstotliwości, \epsilon_\infty \rightarrow \epsilon_{rS}. Ponadto czasy relaksacji mogą być opcjonalnie przesunięte ze względu na zmianę temperatury przy użyciu dowolnego z następujących parametrów Vogel-Fulcher, Arrhenius, Williams-Landel-Ferry, lub Tool-Narayanaswamy-Moyniha lub nawet funkcję przesunięcia zdefiniowaną przez użytkownika.
Jeśli zamiast tego dysponują Państwo danymi eksperymentalnymi dla rzeczywistych i urojonych składowych przenikalności elektrycznej i chcą dopasować do nich model Debye’a, można to zrobić za pomocą funkcji Partial Fraction Fit funkcjonalność w COMSOL® wersja 6.2. Aby uzyskać przewodnik dotyczący korzystania z tej funkcji, proszę zapoznać się z naszym artykułem „Dopasowanie modelu dyspersji Debye’a do danych eksperymentalnych”.
Korzystanie z interfejsu prądów elektrycznych
Uwzględnienie dyspersji w Prądy elektryczne wymaga tylko kilku kroków. Po pierwsze, a Bieżąca ochrona cecha domeny musi zostać dodana i zastosowana do odpowiednich domen. W ramach tej funkcji Typ materiału musi być ustawiony na Solid. Może to być nadal używane do modelowania płynu, przy założeniu, że płyn nie odkształca się.
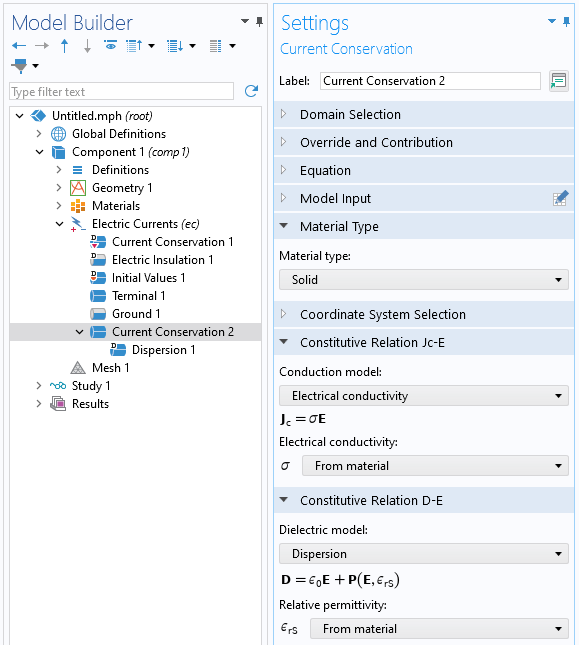
The Bieżąca ochrona funkcja, w której Dyspersja można wybrać model dielektryczny.
Po zmianie Model dielektryczny opcja do Dyspersja, pojawi się dodatkowa podfunkcja. W ramach tej funkcji, gałęzie Multipole Debye jak również zachowanie graniczne, jak pokazano na poniższym zrzucie ekranu. Alternatywnie do wprowadzania biegunów lub gałęzi, możliwe jest również określenie danych relaksacyjnych za pomocą opcji Stała styczna strat model, który jako dane wejściowe przyjmuje styczną strat, częstotliwość środkową i szerokość pasma. Na podstawie tych danych oprogramowanie automatycznie określi liczbę biegunów, czasy relaksacji i względną przenikalność elektryczną. Możliwe jest również użycie prostszego Debye który ma pojedynczy biegun. Efekty termiczne, które powodują przesunięcie czasów relaksacji, można opcjonalnie włączyć za pomocą opcji Efekty termiczne ustawienia.
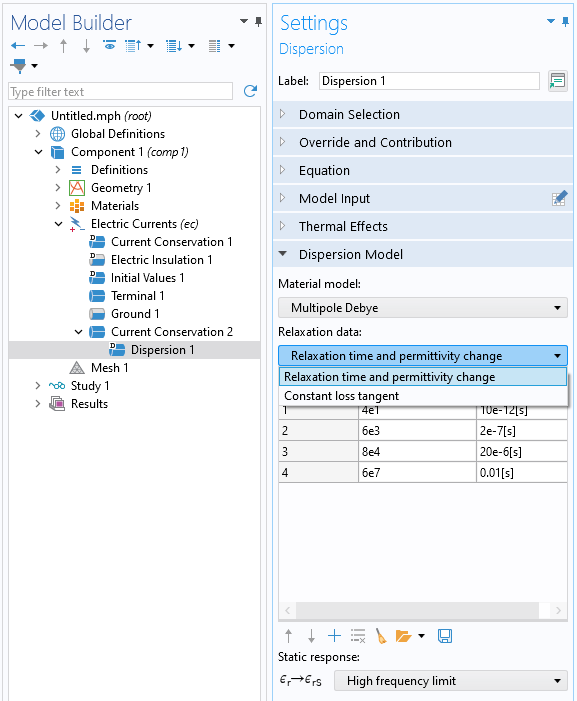
The Dyspersja podfunkcja, w której gałęzie Multipole Debye i określono zachowanie graniczne.
Patrząc na wyniki
Możemy przyjrzeć się, jak dyspersja wpływa na odpowiedź prostego układu, takiego jak równoległy kondensator płytkowy działający w dziedzinie częstotliwości i wypróbować nasze dwa różne materiały umieszczone wewnątrz. Na poniższych wykresach możemy zobaczyć, jak rzeczywiste i urojone składowe impedancji zmieniają się wraz z częstotliwością.
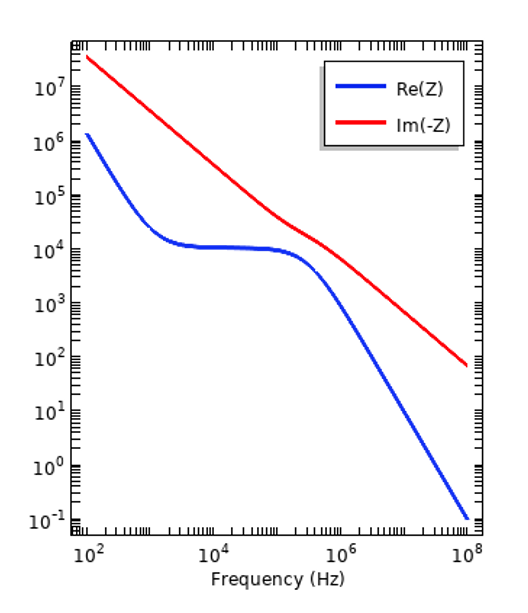
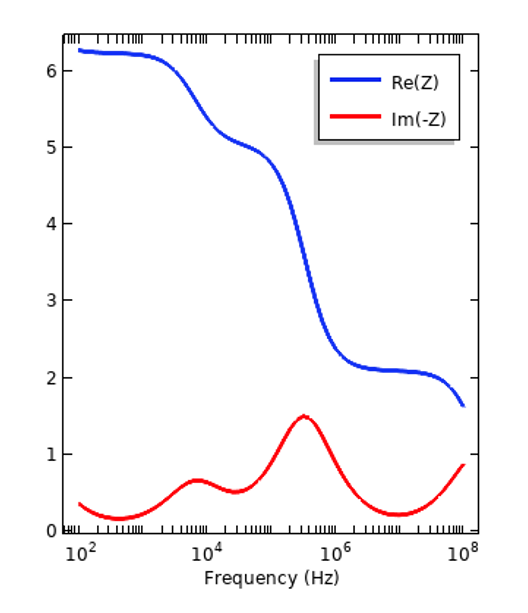
Impedancja równoległego kondensatora płytkowego z próbką izolatora (po lewej) i tkanki (po prawej) wewnątrz. Proszę zauważyć, że wykreślona jest ujemna składowa urojona impedancji.
Możemy również użyć tego samego modelu, aby przyjrzeć się wynikom wzbudzenia tego samego układu w dziedzinie czasu. Przyjrzymy się wyłącznie próbce materiału tkankowego, ponieważ zmiany w odpowiedzi na częstotliwości są bardziej dramatyczne. Konfiguracja materiału dyspersyjnego jest taka sama, ale warto przyjrzeć się różnym sposobom wzbudzania takiego układu. Zaczynamy od pobudzenia układu wygładzonym krokiem w przyłożonym prądzie, narastającym od 0 do 1 A w ciągu 10 ns i obliczamy odpowiedź w ciągu 100 µs, wykreślając napięcie wykryte na zacisku (patrz rysunek poniżej). Wyniki są wykreślane w czasie i w czasie w skali logarytmicznej.
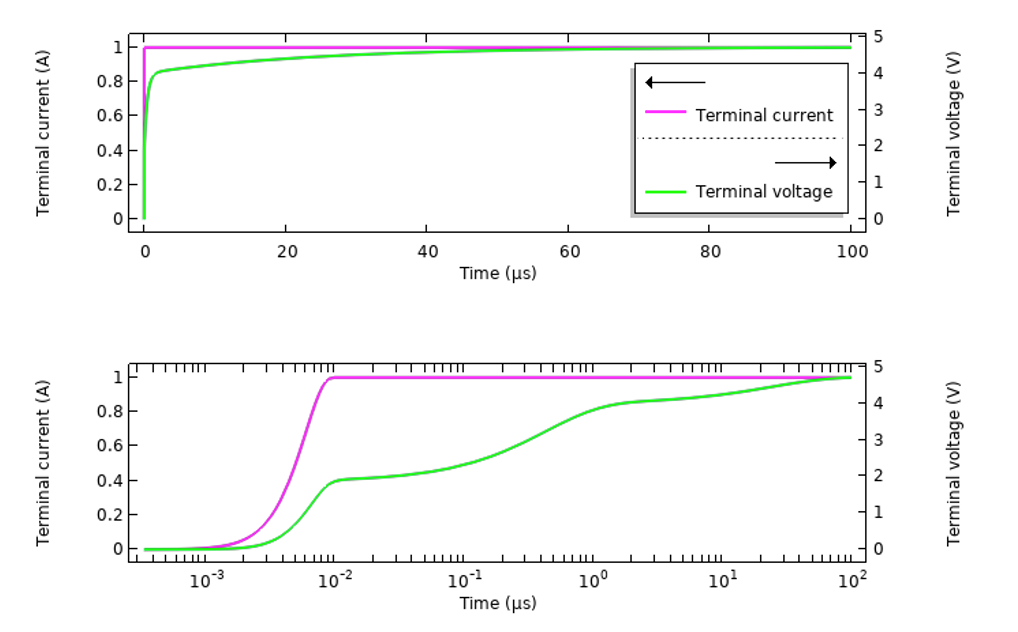
Reakcja przejściowa próbki materiału tkankowego z narzuconym prądem w czasie.
Interesujące jest porównanie tych wyników z modelem wzbudzanym przez podobnie gładki skokowy sygnał napięciowy propagujący się wzdłuż linii transmisyjnej. Poniższe rysunki przedstawiają odpowiedź w postaci zmierzonego prądu i napięcia. Proszę zauważyć, że wykreślony tutaj sygnał napięcia jest sumą padającego wygładzonego sygnału napięcia krokowego i sygnału odbitego od struktury i materiału. Ten całkowity sygnał wykazuje zmienne w czasie zachowanie ze względu na materiał dyspersyjny.
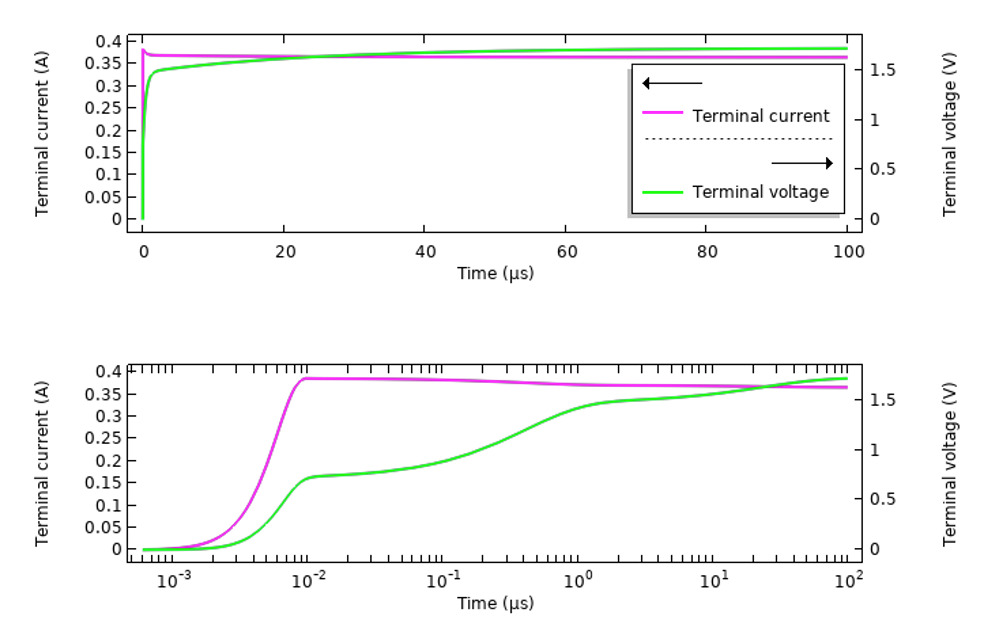
Odpowiedź przejściowa przykładowego materiału tkankowego wzbudzonego przez linię transmisyjną, ze skokowym sygnałem napięciowym.
Uwagi końcowe
Modelowanie dyspersji elektrycznej w obrębie Prądy elektryczne Interfejs jest teraz możliwy i łatwy do skonfigurowania. Ten model materiałowy daje dokładniejszy obraz rzeczywistej odpowiedzi elektrycznej, a także strat w modelach zarówno w dziedzinie częstotliwości, jak i czasu. Ta funkcjonalność jest przydatna do modelowania wielu materiałów.
Warto zauważyć, że modelowanie dyspersji elektrycznej jest również możliwe za pomocą funkcji Elektrostatyka i jest nim od wersji 6.0, w której jest przeznaczony głównie do modelowania stratnych materiałów piezoelektrycznych. Ponadto, w przypadku modelowania przy znacznie wyższych częstotliwościach, moduł RF i moduł optyki falowej zawierają inne modele dyspersji.
Join the forum for Designers!
Your expertise is vital to the community. Join us and contribute your knowledge!
Join the Forum NowShare, learn and grow with the best professionals in the industry.

