Nauka na podstawie paradoksu dwóch kondensatorów: czy istnieje pojemność i indukcyjność?

Join the forum for Designers!

Your expertise is vital to the community. Join us and contribute your knowledge!

Share, learn and grow with the best professionals in the industry.

Paradoks dwóch kondensatorów to prowokacyjny eksperyment myślowy, którego celem jest ujawnienie niektórych ograniczeń modelowania obwodów elektrycznych. Opracowano wiele różnych sposobów rozwiązania tego paradoksu. Dodam rozwiązanie do miksu, które można modelować w COMSOL Multiphysics^® oprogramowanie, a następnie rozwiń je, aby zadać jeszcze bardziej prowokacyjne pytanie i odpowiedzieć na nie: czy istnieje pojemność i indukcyjność? Zanurzmy się!

Paradoks dwóch kondensatorów

Ten eksperyment myślowy jest zwykle przedstawiany w następujący sposób: Rozważmy urządzenie składające się z dwóch równoważnych kondensatorów o pojemności: C, połączone równolegle z otwartym przełącznikiem między nimi. Wszystkie przewody i kondensatory wykonane są z idealnych, doskonale pozbawionych rezystancji, bezstratnych materiałów. Jeden z kondensatorów jest naładowany do potencjału, V_iwięc zgromadzony ładunek wynosi Q = CV_i. Na drugim kondensatorze nie ma różnicy potencjałów, więc nie zgromadził on ładunku. Co się stanie, gdy zamkniesz przełącznik?

Schemat paradoksu dwóch kondensatorów. Jeden kondensator ma różnicę potencjałów pomiędzy okładkami. Co się stanie, gdy przełącznik zostanie zamknięty?

Niektóre prezentacje tego eksperymentu myślowego narzucają błędne podejście i twierdzą, że ładunek na pierwszym kondensatorze przepłynie do drugiego, zmniejszając różnicę potencjałów na pierwszym i zwiększając ją na drugim, aż do osiągnięcia stanu ustalonego – w którym to momencie różnica potencjałów jest taka sama na obu kondensatorach i połowie V_iponieważ ten sam ładunek, Q, jest teraz rozłożony na dwa równoważne kondensatory. To jednak natychmiast prowadzi do paradoksu, ponieważ energia w każdym kondensatorze jest W_C = \frac{1}{2} C \Delta V^2. Jeśli energia początkowa wynosi \frac{1}{2} C V_i^2 a energia końcowa wynosi 2 \frac{1}{2} C\lewo( V_i/2 \prawo)^2 = \frac{1}{4} C V_i^2gdzie poszła druga połowa energii?

Dostępnych jest wiele rozwiązań odwołujących się do wszystkiego, od mechaniki kwantowej po termodynamikę. Wszystkie te rozwiązania są prawdopodobnie ważne z edukacyjnego punktu widzenia. Jednak wiele z nich w sposób ukryty odwołuje się do rzeczywistości, twierdząc, że przewody i kondensatory muszą po prostu mieć pewien opór lub pewną indukcyjność. Ale dlaczego? Przynajmniej w kontekście eksperymentu myślowego rozsądne może być założenie materiałów doskonale bezstratnych, zaniedbując w ten sposób rezystancję. Ale co z indukcyjnością? Czy w kontekście tego eksperymentu myślowego możemy zaniedbać indukcyjność? Prześledźmy to pytanie i zobaczmy, czy dostarcza ono interesującej odpowiedzi…

Proste rozwiązanie paradoksu

Nasze urządzenie składa się z dwóch idealnych, bezstratnych kondensatorów. Ale nawet idealny kondensator musi przestrzennie oddzielać swoje ładunki. Oznacza to, że kondensator musi mieć pewien rozmiar. A jeśli każdy kondensator ma rozmiar, to musi być oddzielony pewną niezerową odległością od drugiego kondensatora. Jeśli więc przerysujemy nieco nasz diagram, zobaczymy, że mamy dwa kondensatory i dwie półpętle o skończonej średnicy z bezstratnego drutu, wzdłuż których może płynąć zmienny w czasie prąd. Ale jak nazywamy taką strukturę? Induktor!

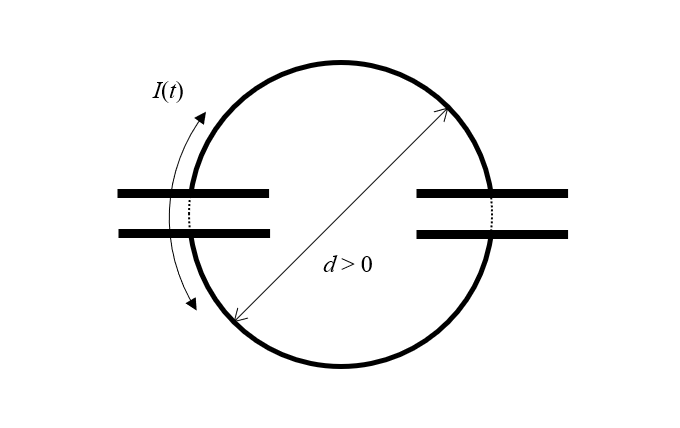
Paradoks można rozwiązać, zdając sobie sprawę, że konstrukcja musi mieć rozmiar niezerowy, a prąd przepływa wokół pętli o skończonej powierzchni, a zatem jest również cewką indukcyjną.

Struktura, którą tutaj narysowaliśmy, musi mieć skończone rozmiary, a co za tym idzie, musi mieć także indukcyjność, o ile istnieje w naszym wszechświecie, gdzie wolna przestrzeń ma przenikalność magnetyczną. Zatem po prostu dlatego, że w naszym obwodzie znajduje się kondensator, w obwodzie musi znajdować się również cewka indukcyjna. Właściwie jest jeszcze lepiej: jeśli mamy cewkę indukcyjną, nawet bezstratną, każdy przepływający przez nią zmienny w czasie prąd doprowadzi do powstania pola elektrycznego istniejącego pomiędzy zwojami cewki indukcyjnej, a zatem każda cewka, którą dodamy do tego Obwód działa również jak kondensator! Moglibyśmy podążać tym tokiem logiki w nieskończoność, ale dla naszych celów wystarczy po prostu zmodyfikować nasz obwód za pomocą pojedynczej cewki indukcyjnej, która ma indukcyjność, L.

Mamy teraz LC obwód, co ma rozwiązanie analityczne, które natychmiast wyjaśnia paradoks: prąd będzie płynął tam i z powrotem pomiędzy kondensatorami i wzdłuż przewodów o skończonej długości, oscylując z częstotliwością określoną wzorem: f=1/\sqrt{2\pi LC}. Nigdy nie będzie rozwiązania w stanie ustalonym, więc nigdy nie będziemy w stanie ocenić samej energii elektrostatycznej. Musimy także wziąć pod uwagę energię wynikającą z poruszających się ładunków, tj. przepływ prądu, Ia to jest dane przez: W_L = \frac{1}{2} LI^2. Suma tej energii elektrycznej i magnetycznej (\frac{1}{2} LI^2 + \frac{1}{2} CV^2) nie ulegnie zmianie w czasie.

Weryfikacja w COMSOL Multiphysics^® Oprogramowanie

Zbudowanie modelu weryfikującego tę sytuację za pomocą COMSOL Multiphysics jest proste^® i moduł RF. Zrobimy to za pomocą Fale elektromagnetyczne, przejściowe interfejs wraz z Elektrostatyka interfejs do obliczania warunków początkowych. Zamodelujemy mały obszar doskonałej próżni z kondensatorami i przewodami znajdującymi się w środku. Płytki kondensatora, przewody i przestrzeń wokół naszej objętości są traktowane jako doskonałe przewodniki elektryczne, co oznacza, że ​​pola elektromagnetyczne nie będą przenikać przez żadne granice. Przewodnik dotyczący konfigurowania takich modeli wyładowań pojemnościowych znajduje się w naszym artykule w Centrum edukacji: „Modelowanie wyładowań pojemnościowych”.

Rozwiązanie tego modelu w dziedzinie czasu i oszacowanie całkowitej energii elektrycznej i magnetycznej pokazuje oczekiwane zachowanie oscylacyjne. Możliwe jest również podzielenie domeny modelowania na różne obszary, aby ocenić całkowitą energię w obszarach wokół dwóch kondensatorów, a także w otaczającej przestrzeni. Ten wykres pokazuje, jak energia oscyluje w przestrzeni i czasie.

Animacja pokazująca prądy na powierzchni płytek i przewodów kondensatora oraz pole magnetyczne w przestrzeni pomiędzy nimi.

Całkowita energia elektryczna i magnetyczna oscyluje w czasie; suma nie zmienia się w tym bezstratnym urządzeniu.

Suma energii elektrycznej i magnetycznej w różnych dziedzinach pokazuje, że energia ta oscyluje w czasie i przestrzeni.

Możemy zaobserwować, że wykresy te nie są czysto sinusoidalne w czasie i powinniśmy zadać sobie pytanie, dlaczego tak jest. Skąd pochodzi ta zawartość o wyższej częstotliwości, tj. falowanie energii w czasie? Wynikają z konstrukcji. Jest całkiem jasne, że obie płytki mają dobrze określoną pojemność, ale istnieje również separacja ładunków ze względu na przewody, a cała konstrukcja znajduje się w cylindrycznej wnęce o częstotliwości rezonansowej. Wszystkie te różne części urządzenia mają pewien wpływ na zachowanie elektromagnetyczne. Każdy wkład może być dość mały, ale zawsze istnieje, gdy weźmiemy pod uwagę strukturę o skończonych rozmiarach.

Zadawanie dodatkowych pytań: czy pojemność i indukcyjność istnieją?

Nadszedł czas, aby zadać bardziej prowokacyjne pytanie na temat tego (lub innego) urządzenia elektromagnetycznego: Czy ma ono pojemność lub indukcyjność? Wyraźnie widzieliśmy, że to konkretne urządzenie ma jedno i drugie. Ale co by było, gdybyśmy to zmodyfikowali, dodając bardzo mocny materiał dielektryczny pomiędzy płytkami kondensatora? To spowodowałoby znacznie większą pojemność, ale pozostawiłoby indukcyjność bez zmian. A gdybyśmy znacznie zwiększyli pojemność, czy moglibyśmy powiedzieć, że indukcyjność nie ma znaczenia?

Krótko mówiąc: nie, nigdy nie powinniśmy myśleć o urządzeniu elektrodynamicznym jako o urządzeniu wyłącznie pojemnościowym lub czysto indukcyjnym. W urządzeniu elektrodynamicznym zawsze będzie energia elektryczna wynikająca z przestrzennego rozdzielenia ładunków i energia magnetyczna wynikająca z ruchu ładunków. Chociaż czasami możemy konstruować hipotetyczne sytuacje, w których można zignorować jedną lub drugą, zawsze musimy pamiętać, że dokonujemy uproszczenia mentalnego.

Co więcej, wszystkie rzeczywiste materiały mają również pewien skończony opór, więc aby być bardziej realistycznym, powinniśmy mówić o wszystkim, co ma impedancję – i wtedy czasami wpadamy w jeszcze większe kłopoty. W przypadku modelu w dziedzinie częstotliwości istnieje bardzo znane wyrażenie na impedancję urządzenia elektrycznego:

Z = R + j\omega L -j\frac{1}{\omega C}

Opór, Rw tym wyrażeniu jest miarą tego, jak energia kinetyczna poruszających się ładunków, tj. prąd, jest przekształcana w energię cieplną.

Równanie to można natychmiast rozpoznać jako odnoszące się do tłumionego oscylatora harmonicznego o jednym stopniu swobody, co jest jednym z najlepiej zbadanych problemów inżynierii i fizyki. Wiemy, że na podstawie tego wyrażenia możemy obliczyć częstotliwość rezonansową i współczynnik jakości takiego oscylatora, a także wiemy, że rzeczywiste urządzenia mają podstawowy współczynnik rezonansu i jakości. To kusi nas, aby zrównać te dwa elementy i spróbować zredukować rzeczywiste urządzenie elektryczne o skończonych rozmiarach do jednego oporu, pojemności i indukcyjności. Jest to błąd koncepcyjny i nigdy nie jest prawidłowy, ponieważ powyższe wyrażenie na impedancję ma zastosowanie tylko do urządzenia o nieskończenie małych rozmiarach.

Każde rzeczywiste urządzenie ma skończone rozmiary i gdy działa w rezonansie, energia elektryczna i magnetyczna zmienia się w czasie i przestrzeni, jak widzieliśmy na powyższych wykresach. Dlatego równoważny model obwodu wymaga co najmniej trzech węzłów, co najmniej trzech węzłów, chociaż czasami znacznie więcej. Wracając myślami do naszego modelu fizycznego dwóch kondensatorów i zakładając, że okładka każdego kondensatora jest reprezentowana przez węzeł w obwodzie elektrycznym, widzimy, że równoważny model obwodu musiałby być co najmniej tak skomplikowany, jak obwód na rysunku poniżej, z czterema węzłami. Należy zauważyć, że równolegle do indukcyjności drutów dodano niewielką pojemność, ponieważ wzdłuż drutów następuje również oddzielenie ładunku.

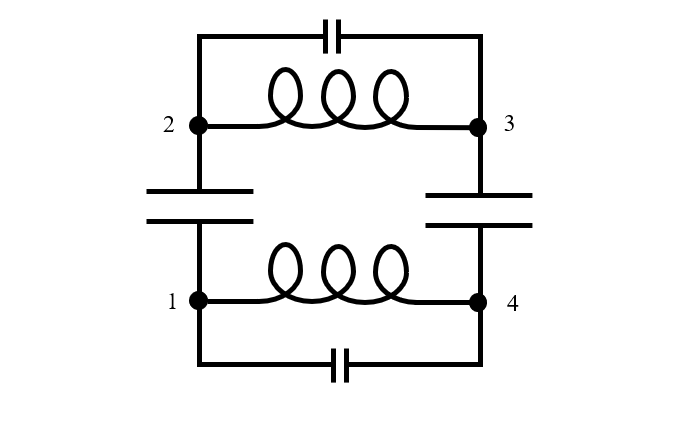
Równoważny model obwodu dwóch bezstratnych kondensatorów o skończonych rozmiarach połączonych szeregowo.

Miejmy nadzieję, że z tego przykładu wynika, że ​​skonstruowanie równoważnego modelu obwodu, który sprawdza się w pobliżu rezonansu, może szybko stać się bardzo skomplikowane i wymagać wnikliwości fizycznej, dużego doświadczenia z podobnymi urządzeniami i modelowania numerycznego.

Wracając do pierwotnego pytania, można argumentować, że pojemność, indukcyjność, a nawet rezystancja to pojęcia, które nie istnieją same w sobie – że istnieją jedynie w połączeniu ze sobą. Chociaż czasami możemy zmniejszyć zależną od częstotliwości impedancję urządzenia do pojedynczego oporu, pojemności i/lub indukcyjności, takie uproszczenia obowiązują tylko w przypadku częstotliwości poniżej rezonansu urządzenia. Mając to na uwadze, możemy uniknąć wszelkiego rodzaju pułapek, począwszy od zabawnego paradoksu dwóch kondensatorów po znacznie bardziej frustrująco złożone problemy w świecie rzeczywistym.

Uwagi końcowe

Zastosowaliśmy tutaj klasyczny eksperyment myślowy, aby zrozumieć, dlaczego impedancji urządzenia elektromagnetycznego pracującego w pobliżu rezonansu nie można rozłożyć na pojedynczy równoważny opór, pojemność i indukcyjność. Eksperymenty myślowe, takie jak paradoks dwóch kondensatorów, są cenne dla poszerzenia naszej wiedzy o elektromagnetyzmie i interpretacji wyników naszych modeli obliczeniowych.

Dalsze czytanie

Chcesz dowiedzieć się, jak modelowanie i symulacja można wykorzystać do rozwiązywania innych łamigłówek? Sprawdź inne przykłady na blogu COMSOL:

Join the forum for Designers!

Your expertise is vital to the community. Join us and contribute your knowledge!

Share, learn and grow with the best professionals in the industry.