Optymalizacja kształtu i topologii stopniowych łożysk wzdłużnych

Join the forum for Designers!

Your expertise is vital to the community. Join us and contribute your knowledge!

Share, learn and grow with the best professionals in the industry.

Łożyska wzdłużne stopniowe są stosowane do przenoszenia obciążeń osiowych w maszynach wirujących, a ponieważ nośność zależy od geometrii, można użyć optymalizacji kształtu i topologii, aby zmaksymalizować nośność łożyska. Optymalizacja kształtu polega na zmianie kształtu stopni w łożysku, podczas gdy optymalizacja topologii wykorzystuje niejawny opis geometrii, dzięki czemu liczba stopni może się zmieniać.

Wprowadzenie

Łożyska wzdłużne krokowe można modelować przy założeniu, że:

1. Grubość warstwy płynu jest znacznie mniejsza niż wymiary poprzeczne łożyska
2. Efekty bezwładności można zignorować w porównaniu z efektami ścinania ze względu na cienką warstwę smaru
3. Siły ciała są pomijalne
4. Środek smarny jest newtonowski
5. Prędkości poza płaszczyzną są pomijalne, ponieważ współczynnik kształtu filmu olejowego jest duży
6. Wielkość prędkości zależy analitycznie od współrzędnej pozapłaszczyznowej

Założenia 2-4 oznaczają, że równanie Naviera-Stokesa można uprościć do równania Stokesa, a założenia 5-6 pozwalają nam dalej zakładać, że prędkość płynu jest proporcjonalna do gradientu ciśnienia. Biorąc pod uwagę te punkty, a także inne założenia, równanie rządzące zredukowałoby się do standardowego równania Reynoldsa dla ciśnienia, ale tutaj zamiast tego zastosowano teorię Jakobssona-Floberga-Olssona (JFO), aby uwzględnić kawitację. Mogą to Państwo zobaczyć na poniższym szkicu rozkładu ciśnienia. Ciśnienie jest wykreślone jako kolorowa linia wzdłuż średniego promienia, a jego współrzędna poza płaszczyzną jest proporcjonalna do ciśnienia. Ciśnienie spada, gdy płyn przechodzi przez skurcz, i nie zaczyna rosnąć, dopóki nie zbliży się do następnego kroku w następującym rowku.

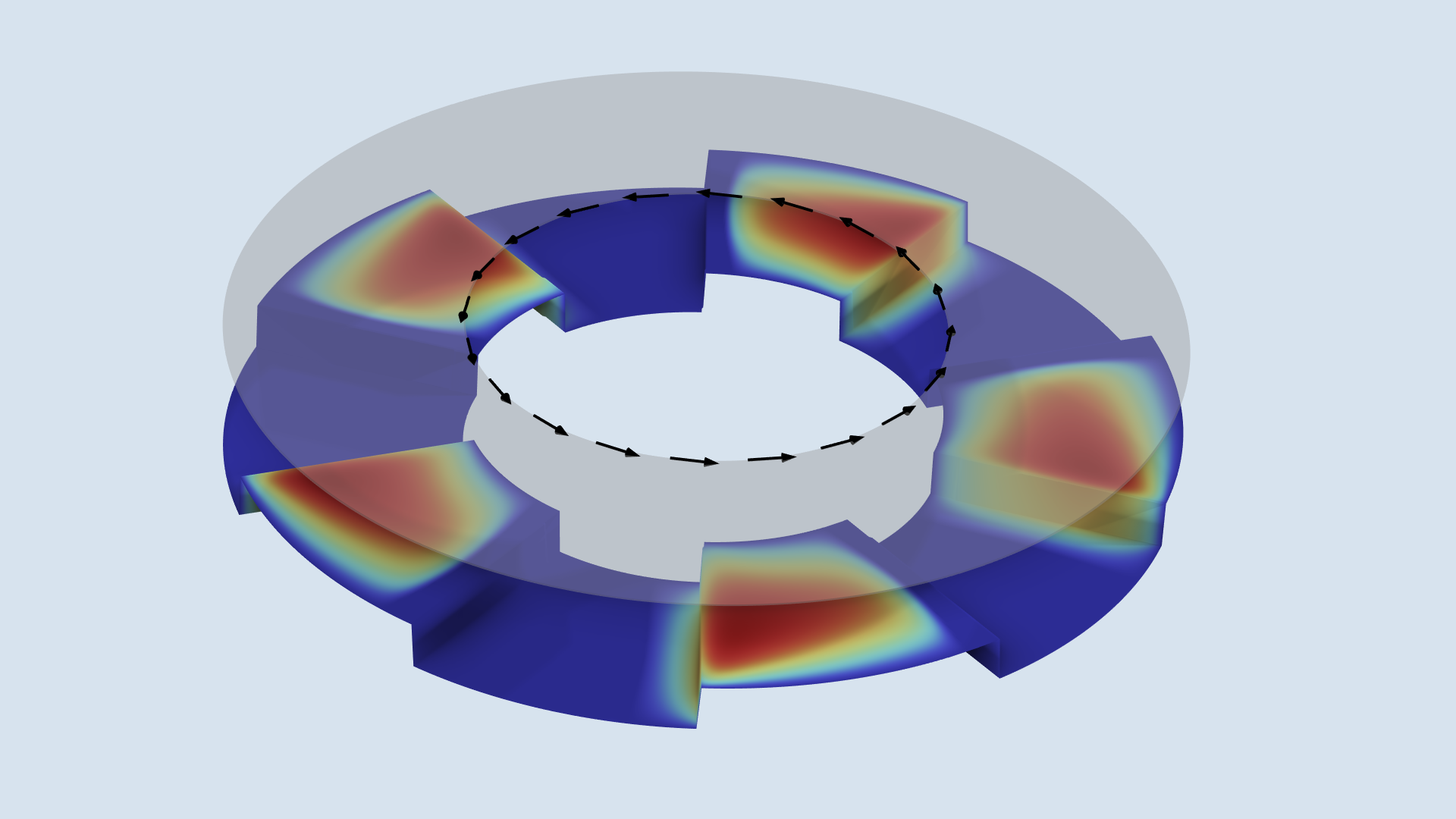
Łożysko oporowe schodkowe jest naszkicowane z kołnierzem. Kolory pokazują ciśnienie. Proszę zauważyć, że stopnie nie są modelowane w wyraźnym trójwymiarowym sensie, więc wykres nie przedstawia siatki obliczeniowej.

Fizyka łożyska jest modelowana za pomocą funkcji Łożysko hydrodynamiczne interfejs w COMSOL Multiphysics^® oprogramowanie. Ta funkcja nie uwzględnia wyraźnie wymiaru poza płaszczyzną. Zamiast tego używana jest geometria płaska, a zmiana grubości jest uwzględniana bezpośrednio w równaniu, jak pokazano na powyższym obrazku.

Nośność zależy od rozkładu ciśnienia, który z kolei zależy od kształtu stopni. Dlatego warto zastosować optymalizację kształtu, aby zmaksymalizować nośność,

\mathrm{obj}=\int_\Omega \boldmath{f}_\textrm{c}\,d\Omega,

gdzie \boldmath{f}_\text{c} to rozłożona siła działająca na kołnierz, która składa się ze składowych Poiseuille’a, Couette’a i ciśnienia normalnego. Jak wspomniano wcześniej, model uwzględnia kawitację, ale nie podjęto próby ograniczenia jej nasilenia.

Optymalizacja kształtu

Optymalizacja kształtu polega na zmianie istniejącego kształtu przy użyciu deformacji siatki. Istnieje wiele wbudowanych funkcji do osiągnięcia tego celu w oprogramowaniu Optymalizacja kształtu i w tym konkretnym przypadku, interfejs trzeciego rzędu Polynomial Shell jest używana, gdy deformacja poza płaszczyzną jest wyłączona. Jest to używane dla jednego zestawu przednich i tylnych krawędzi klocków, a deformacja siatki jest kopiowana do innych klocków za pomocą funkcji Symetria sektora funkcja.

Przedstawione tutaj podejście ustala położenie punktów na okrągłych granicach, ale możliwe jest umożliwienie tym punktom przesuwania się wzdłuż okrągłych granic. Wymaga to jednak zastosowania modelowania opartego na równaniach i oddzielnego Funkcja kontrolna dla końcowych i przednich krawędzi stopni, co komplikuje konfigurację. Zwiększona swoboda projektowania prowadzi tylko do nieznacznie lepszej wydajności, dlatego ten wpis na blogu koncentruje się na prostszym podejściu, ale alternatywne sformułowanie jest zawarte w bibliotece aplikacji COMSOL^® w wersji 6.1 i nadal można ją pobrać z Galerii aplikacji.

Wynik optymalizacji kształtu pokazano na poniższym rysunku. Wynik zależy od maksymalnego odkształcenia krawędzi oraz początkowego kąta rowka. Optymalizacja daje projekt, który spycha olej wzdłuż środka, zanim zostanie on przepchnięty przez podkładkę.

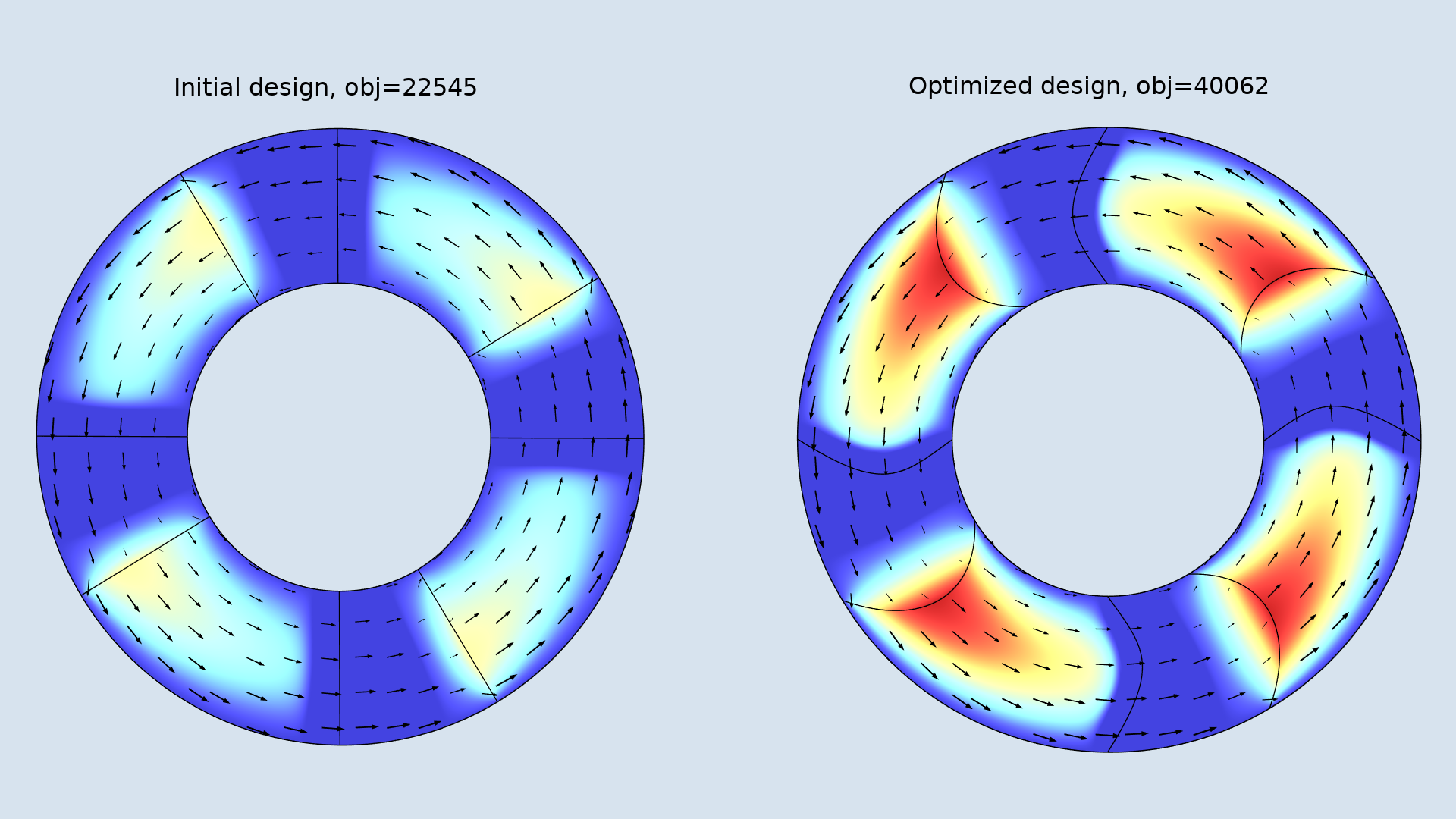
Pokazano projekt początkowy (po lewej) wraz z projektem zoptymalizowanym (po prawej). Strzałkami zaznaczono średnią prędkość płynu, a kolorami rozkład ciśnienia.

Dobrą praktyką jest przeprowadzenie weryfikacji poprzez ponowne przetworzenie w zdeformowanej konfiguracji. Weryfikacja nie ujawnia żadnych problemów numerycznych, co można zobaczyć w wersji Application Library tego modelu.

W tym przykładzie maksymalne odkształcenie i kąt rowka są ustalone jako niezależne od liczby podkładek. Z tego powodu optymalna liczba podkładek wynosi cztery, jak pokazano poniżej.

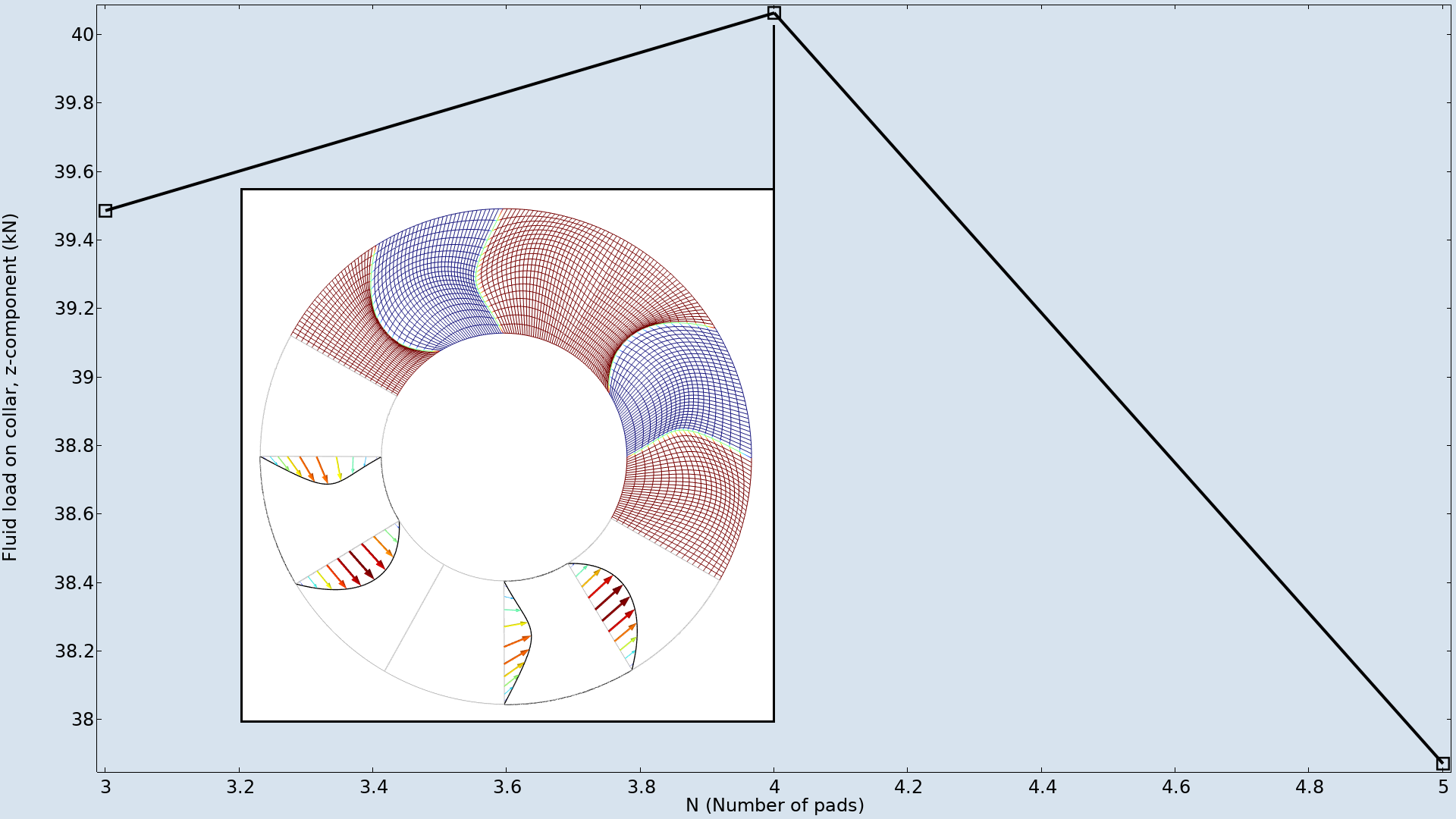
Optymalizacja kształtu jest przeprowadzana dla różnej liczby podkładek, a uzyskane cele są przedstawione na wykresie. Maksimum występuje dla czterech podkładek, a wstawka pokazuje, jak deformowana jest siatka.

Optymalizacja kształtu działa tak samo niezależnie od fizyki, co ułatwia jej konfigurację. Zniekształcenia siatki wprowadzane przez optymalizację kształtu są ograniczone, aby uniknąć problemów numerycznych, ale użytkownik może swobodnie eksperymentować z równowagą między dużą swobodą projektowania z dużą poprawą wydajności i małą swobodą projektowania z solidną optymalizacją. W każdym razie, zoptymalizowany projekt jest bardzo zależny od początkowej geometrii w tym sensie, że topologia (a tym samym liczba kroków) może być tylko danymi wejściowymi do optymalizacji, a nie danymi wyjściowymi. Optymalizacja topologii może rozwiązać ten problem poprzez wprowadzenie niejawnego opisu geometrii. Metoda ta może mieć swoje wady, ale w tym przypadku może być stosowana bez większych komplikacji.

Optymalizacja topologii

Optymalizacja topologii działa poprzez wprowadzenie zmiennej projektowej, \theta_cdla każdego elementu obliczeniowego. Jest to ograniczone do zamkniętego przedziału między 0 a 1. Wymagane jest, aby zmienna była powiązana z fizyką w taki sposób, że:

1. Gdy zmienna projektowa jest równa 0, rozwiązywane są równania rządzące odpowiadające rowkowi
2. W przypadku, gdy zmienna projektowa jest równa 1, rozwiązywane są równania rządzące odpowiadające podkładce.
3. W przypadku, gdy zmienna projektowa wynosi od 0 do 1, rozwiązywane jest równanie rządzące łączące równania odpowiadające rowkowi i podkładce

Jedyną różnicą między rowkami i podkładkami jest grubość filmu olejowego, h_f, więc wyżej wymienione wymagania są spełnione poprzez uzależnienie tej grubości od zmiennej projektowej. W przypadku innych problemów z optymalizacją topologii, szczegóły trzeciego punktu wymagają szczególnej uwagi, ale w tym przypadku prosta interpolacja liniowa okazuje się wystarczająca:

h_f &=& h_\mathrm{pad} + (h_\mathrm{groove}-h_\mathrm{pad})\theta_f,

gdzie \theta_f jest polem używanym w fizyce, podczas gdy \theta_c jest polem zmiennej sterującej. W tym przypadku można ustawić \theta_c = \theta_f, ale zbieżność można poprawić, wprowadzając filtr, który usuwa małą skalę długości w polu zmiennej sterującej. Daje to również gładsze wyniki oceny i weryfikacji wyników. Filtr można wyrazić jako równanie różniczkowe cząstkowe (filtr Helmholtza),

\theta_f &=& R_\mathrm{min}^2\mathbf{\nabla}^2 \theta_f+\theta_c \quad \mathrm{and} \quad 0 \leq \theta_c \leq 1,

gdzie R_\mathrm{min} to minimalna skala długości. (Aby uzyskać więcej informacji na temat filtra Helmholtza i regularyzacji dla optymalizacji topologii, proszę zapoznać się z naszym wpisem na blogu „Wykonywanie optymalizacji topologii za pomocą metody gęstości”).

Optymalizacja może dowolnie ustawiać zmienną projektową na wartości pośrednie, a w tym przypadku można to interpretować jako pośrednią grubość warstwy oleju, ale często wartości pośrednie nie mają wyraźnej reprezentacji fizycznej – a przynajmniej nie reprezentacji, która ma praktyczne znaczenie. Problem ten wydaje się z natury dobrze postawiony w tym sensie, że optymalizacja automatycznie znajduje rozwiązanie bez pośrednich zmiennych projektowych, co oznacza, że istnieje wyraźne rozróżnienie między podkładkami a rowkami.

Optymalizację topologii najlepiej rozpocząć od jednolitej wartości zmiennej projektowej. Skutkuje to projektem z czterema podkładkami, ale można również rozpocząć od niejednolitego projektu, aby promować inne lokalne optimum, jak widać na poniższym rysunku.

Optymalizacja topologii jest inicjowana za pomocą różnych niejednolitych projektów początkowych w celu promowania określonych topologii. Wykres wskazuje, że optymalna liczba podkładek to cztery.

W przypadku tych ustawień wydaje się, że istnieje dobra zgodność między wynikami optymalizacji kształtu i topologii.

Po przeprowadzeniu optymalizacji topologii dobrą praktyką jest również przeprowadzenie symulacji weryfikacyjnej, ale podczas gdy weryfikacja optymalizacji kształtu służy do sprawdzenia problemów numerycznych związanych z odkształconymi elementami, weryfikacja optymalizacji topologii służy do sprawdzenia problemów związanych z niejawną reprezentacją geometrii. Weryfikacja optymalizacji topologii wykorzystuje zatem jawną reprezentację geometrii, co daje znacznie lepszą funkcję celu, co wskazuje, że istnieje znaczny koszt niejawnego opisu geometrii. Analizując to dalej, okazało się, że możliwe jest uzyskanie znacznie lepszego celu przy optymalizacji topologii, jeśli użyje się drobniejszej siatki, jak pokazano na poniższej animacji, gdzie projekt został zainicjowany w celu promowania topologii z 16 podkładkami. Wynikowy projekt jest jakościowo podobny do poprzednich projektów i jest podobny do łożysk oporowych rowkowanych w jodełkę.

Optymalizacja topologii łożyska zainicjowanego z 16 podkładkami.

Wszystkie optymalizacje uwzględniają stały kierunek obrotu, co jest wyraźnie widoczne w zoptymalizowanych projektach. Początkowy projekt jest symetryczny względem osi obrotu, więc jasne jest, że wydajność można uzyskać poprzez rozluźnienie tego ograniczenia. Z tego powodu można również oczekiwać mniejszych celów, jeśli oba kierunki obrotu zostaną uwzględnione w optymalizacji.

Wnioski

Omówiliśmy tutaj, w jaki sposób można wykorzystać optymalizację kształtu i topologii do projektowania łożysk oporowych. Konfigurację fizyki i omawianą tutaj optymalizację można przeanalizować w tych modelach i związanej z nimi dokumentacji:

Join the forum for Designers!

Your expertise is vital to the community. Join us and contribute your knowledge!

Share, learn and grow with the best professionals in the industry.