Tworzenie aplikacji Metalens Design za pomocą COMSOL Multiphysics®

Join the forum for Designers!

Your expertise is vital to the community. Join us and contribute your knowledge!

Share, learn and grow with the best professionals in the industry.

Ten wpis na blogu jest Państwa przewodnikiem po budowaniu prostej i edukacyjnej aplikacji symulacyjnej do projektowania dwuwymiarowych odblaskowych metalenów składających się z szeregu szklanych nanosłupków o różnych średnicach na metalowym podłożu. Aby zbudować tę aplikację, użyjemy kreatora aplikacji w COMSOL Multiphysics^® oprogramowanie. Aplikacja najpierw znajduje optymalne parametry meta-powierzchni dla danej długości fali, a następnie oblicza zależność między średnicą nanofilar a względnym przesunięciem fazowym. Na tej podstawie aplikacja automatycznie tworzy geometrię dla metalenów, a na koniec przeprowadza badanie w dziedzinie częstotliwości na sfinalizowanej geometrii w celu obliczenia pola elektrycznego wokół ogniska.

Co to jest metalen?

W ostatnich latach metamateriały stały się popularnym tematem badań w dziedzinach obejmujących rozwiązania równania falowego, takich jak fotonika i akustyka. Metamateriał to materiał kompozytowy o sztucznej strukturze (jednostka strukturalna jest czasami nazywana „metaatomem”), zwykle mniejszej niż długość fali. Z tego powodu metamateriały oddziałują z polami elektromagnetycznymi jak jednorodny materiał o właściwościach materiałowych, które różnią się od właściwości materiałów składowych. Prozaicznym tego przykładem jest krata w drzwiach kuchenki mikrofalowej – metalowa płytka z otworami wypełnionymi powietrzem jest metamateriałem o właściwościach, których nie wykazuje ani lita metalowa płytka, ani powietrze: jest w większości przezroczysta dla światła widzialnego o krótkiej długości fali, jednocześnie blokując całkowicie mikrofale o długiej długości fali.

Oprócz tego, że metamateriały mogą oferować właściwości jakościowe, jakich nie ma żaden znany „prawdziwy” materiał, główną zaletą metamateriałów jest to, że ich właściwości można dostroić ilościowo – zwykle w szerokim zakresie – poprzez zmianę parametrów geometrycznych struktury. Wiele technik opracowanych do produkcji półprzewodników, takich jak fotolitografia, ma zastosowanie do wytwarzania metametamateriałów. Elementy optyczne wykonane z takich metamateriałów są bardzo poszukiwane do zastosowań takich jak sprzęt mikroskopowy i technologia wirtualnej rzeczywistości.

Zbliżenie na kratkę w drzwiczkach kuchenki mikrofalowej.

W tym wpisie na blogu skupimy się na odblaskowych metalenach: płaskiej matrycy składającej się ze szklanych nanosłupków na metalowym podłożu, zaprojektowanej tak, aby działała jak wklęsłe lustro. Chociaż wydaje się, że „metamirror” byłoby bardziej odpowiednią nazwą, ważne jest, aby docenić fakt, że zasada działania tego urządzenia nie jest tylko konwencjonalnym odbiciem, ale czymś znanym jako anomalne odbicie, gdzie odbita fala również ulega przesunięciu fazowemu zależnemu od współrzędnych. Metalens ma zalety w porównaniu z konwencjonalnymi urządzeniami optycznymi, takimi jak soczewki i lustra, w tym:

• Metalen może mieć grubość ułamka mikrona, co pozwala na miniaturyzację urządzeń optycznych
• Pojedyncza metapowierzchnia może być zaprojektowana tak, aby robić znacznie więcej niż tylko skupiać światło, więc możliwe jest połączenie wielu konwencjonalnych urządzeń optycznych w jedno ultracienkie metaurządzenie
• Metamateriały mogą zapewnić lepszą wydajność w niektórych zakresach długości fal, takich jak ultrafiolet (UV)

Dokładniej, rozważymy dwuwymiarowe metaleny składające się z nanosłupków dwutlenku krzemu o jednakowej wysokości, Hi okres, P, ale o różnej średnicy, D(x)umieszczonej na płaskim metalowym podłożu, jak pokazano na poniższym rysunku. Dla uproszczenia rozważamy tylko falę płaską przy normalnym padaniu (poruszającą się w kierunku ujemnym). y kierunek), spolaryzowany w kierunku poza płaszczyzną.

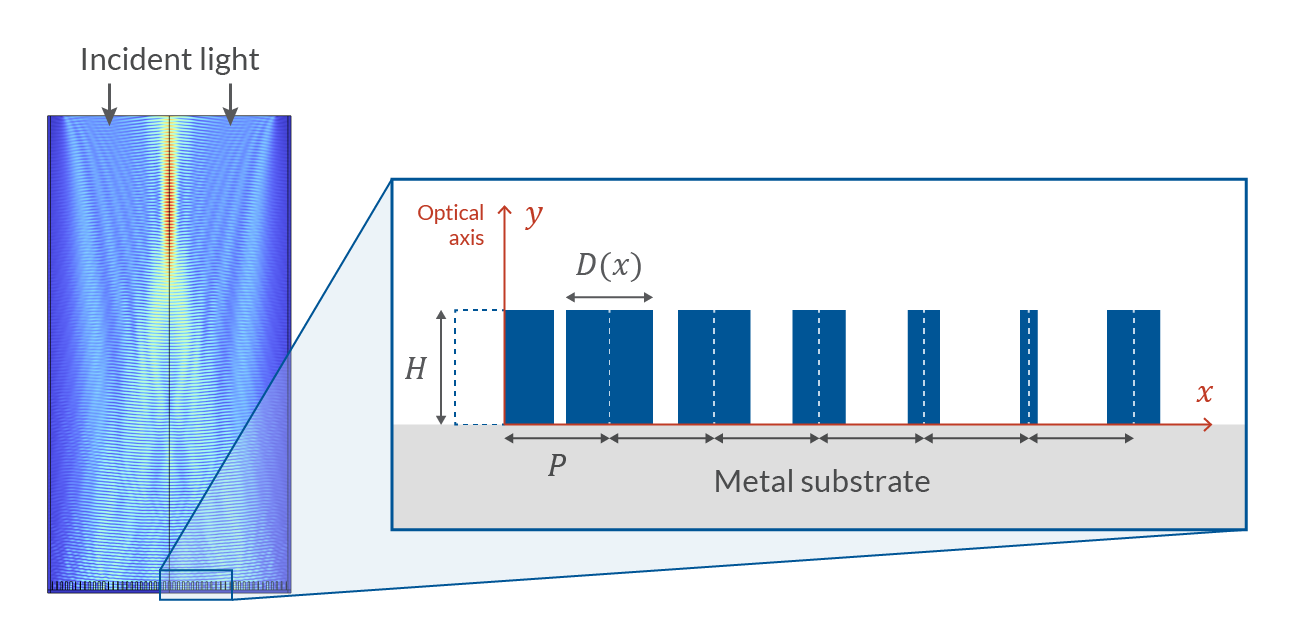
Z matematycznego punktu widzenia, zwierciadło wklęsłe jest urządzeniem, które, biorąc pod uwagę padającą falę płaską, lokalnie przesuwa fazę fali tak, że staje się ona falą sferyczną zbiegającą się w punkcie, tj. ognisku. Intuicyjnie możemy sobie wyobrazić, że wraz ze wzrostem grubości filarów, odbita fala odbiera większe przesunięcie fazowe ze względu na wyższy współczynnik załamania filarów w porównaniu z otaczającym powietrzem, ale jeśli chcemy zbudować działający metalens, musimy uzyskać dokładną zależność ilościową między średnicą a względnym przesunięciem fazowym \Delta \Phi (D), jak opisano w następnej sekcji. Przyjęte tutaj podejście opiera się na Ref. 1.

Symulacja komórki elementarnej

Skuteczny sposób na uzyskanie \Delta \Phi (D) jest obliczenie przesunięcia fazowego spowodowanego jednolitą okresową siatką, w której wszystkie nanosłupki mają średnicę Di przeszukiwać zakres wartości średnicy. (Więcej informacji na temat modelowania struktur okresowych można znaleźć tutaj.) Pozwala nam to na zastosowanie okresowych warunków brzegowych, dzięki czemu będziemy musieli symulować tylko jedną komórkę siatki. Użycie okresowego warunku brzegowego portu do wzbudzenia fali padającej oznacza, że mamy wygodny dostęp do przesunięcia fazowego fali poprzez argument złożonego parametru S S_{11}.

Aby zbudować działający metalen, musimy być w stanie przesunąć lokalną fazę fali o dowolną wartość pomiędzy 0 oraz 2\pi radianów. Dlatego najpierw musimy znaleźć wartości H, Poraz minimalną i maksymalną średnicę, D_\mathrm{min} oraz D_\mathrm{max}, takie że \Delta \Phi ( D_\mathrm{max} ) – \Delta \Phi ( D_\mathrm{min} ) = 2 \pizachowując możliwie wysoki współczynnik odbicia. Jest to problem optymalizacji w dziedzinie częstotliwości. Etap optymalizacji wymaga tylko wyników w punktach końcowych przemiatania, więc możemy pominąć etapy pośrednie, co przyspiesza obliczenia. Ponieważ wiemy, że im węższe są kolumny, tym szerszy jest zakres przesunięć fazowych i że najmniejsze możliwe przesunięcie fazowe jest możliwe. D_\mathrm{min} podlega ograniczeniom produkcyjnym, nie traktujemy D_\mathrm{min} jako parametr kontrolny. Zamiast tego, D_\mathrm{min} jest stałym parametrem o wartości 20~\mathrm{nm} dla większości długości fal (dla długości fal około 300~\mathrm{nm} i poniżej, 10~\mathrm{nm} proszę użyć zamiast tego, aby uzyskać dobre wyniki). Interesuje nas tylko faza względna, więc nasza funkcja celu powinna wyglądać mniej więcej tak

\left| \mathrm{arg} \left[ \frac{S_{11}( D_\mathrm{max} )}
{S_{11}( D_\mathrm{min} )} \right]-2\pi\right|.

Jednak to wyrażenie nie jest gotowe do użycia w interfejsie użytkownika, ponieważ oprogramowanie używa konwencji znaków e^{-iky} dla fali płaskiej propagującej się w kierunku dodatnim y i definiuje fazę liczby zespolonej od -\pi do \pi. Podczas korzystania z COMSOL^®i po dodaniu wymaganych operatorów, aby odnieść się do rozwiązań dla D=D_\mathrm{min} oraz D=D_\mathrm{max}otrzymujemy wyrażenie pokazane na poniższym rysunku. Dodaliśmy również termin obejmujący współczynniki odbicia uzyskane z tych dwóch rozwiązań do wyrażenia Funkcja celu, która pomaga uniknąć trybów rezonansowych i zapewnić wysoką wydajność. Jeśli chcą Państwo dowiedzieć się więcej na temat optymalizacji, zapraszamy do zapoznania się z naszym wpisem na blogu na temat optymalizacji kształtu w elektromagnetyce lub naszym kursem na żądanie Optymalizacja w COMSOL Multiphysics.^®.

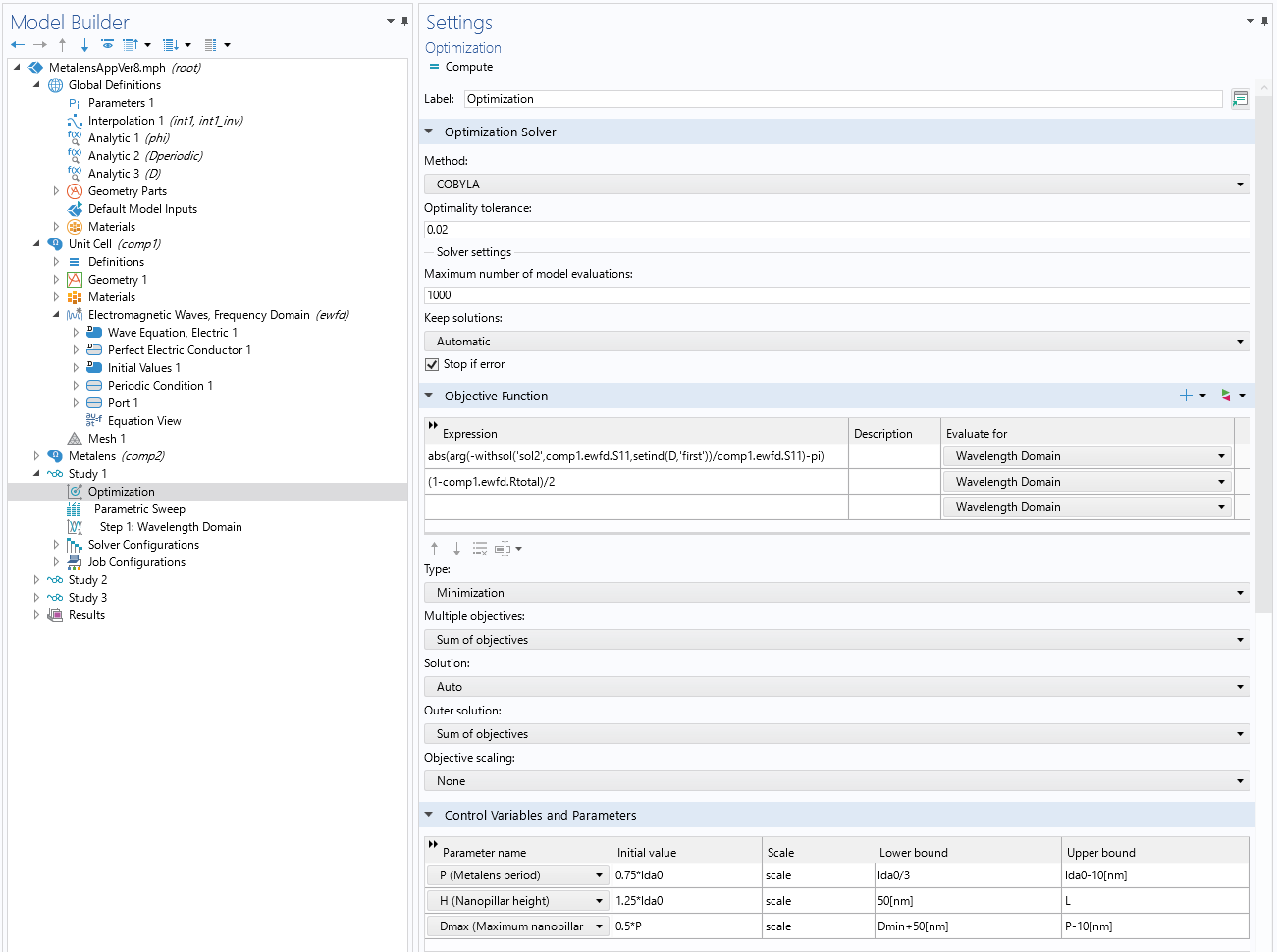
Ustawienia używane w badaniu optymalizacyjnym (Badanie 1). Etap optymalizacji wykorzystuje wyniki przeszukiwania w punktach końcowych, więc musimy umieścić Parametric Sweep krok po Optymalizacja krok, jak pokazano w drzewie Model Builder, i proszę użyć opcji withsol() i sentind() aby zaimplementować pożądaną funkcję celu. Dodaliśmy również drugie wyrażenie dla współczynników odbicia do funkcji Funkcja celu ustawienia.

Jedyne, co pozostało do zrobienia, to uruchomienie pełnego przemiatania ze zoptymalizowanymi wartościami parametrów, aby uzyskać przesunięcie fazowe dla wartości pośrednich między D_\mathrm{min} oraz D_\mathrm{max}. Wynik powinien wyglądać jak na poniższym rysunku: ładne, monotonicznie rosnące przesunięcie fazowe z wysokim współczynnikiem odbicia w całym zakresie średnic. Następnie nadszedł czas na zbudowanie metalenów w oparciu o te wyniki.

Wykres wyników przemiatania komórki elementarnej dla 400~\mathrm{nm}wykazując przesunięcie fazowe, które wzrasta monotonicznie od 0 do 2\pi zachowując wysoki współczynnik odbicia w całym zakresie średnic nanoprętów.

Symulacja Metalens

Zanim będziemy mogli zbudować geometrię Metalens, musimy przekształcić funkcję przesunięcia fazowego \Delta \Phi (D) w funkcję rozkładu średnicy nanofilar D(x), gdzie x jest odległością od osi optycznej. Wiemy, że idealne zwierciadło skupiające stosuje następujące przesunięcie fazowe do fali płaskiej przy normalnym padaniu:

\Delta \phi (x) = – \frac{2\pi}{\lambda_0}\sqrt{f^2+x^2}+\frac{2\pi}{\lambda_0}\sqrt{f^2+R^2}.

Proszę, f oraz R to odpowiednio ogniskowa i promień metalenów. Dla wygody zdecydowaliśmy się zdefiniować \Delta \phi (x) takie, że \Delta \phi (R) =0. Reszta jest kwestią kilku manipulacji numerycznych: zakładając, że przesunięcie fazowe jest monotoniczne, możemy odwrócić \Delta \Phi (D) aby otrzymać \Delta \Phi ^{-1} (\phi) \equiv D( \phi )proszę dodać okresowość, aby D( \phi \pm 2n\pi ) =D( \phi )i utworzyć funkcję złożoną z \Delta \phi (x) więc otrzymujemy D(\phi(x)) \equiv D(x) . Przykład tego, jak powinno to wyglądać, pokazano na poniższym rysunku.

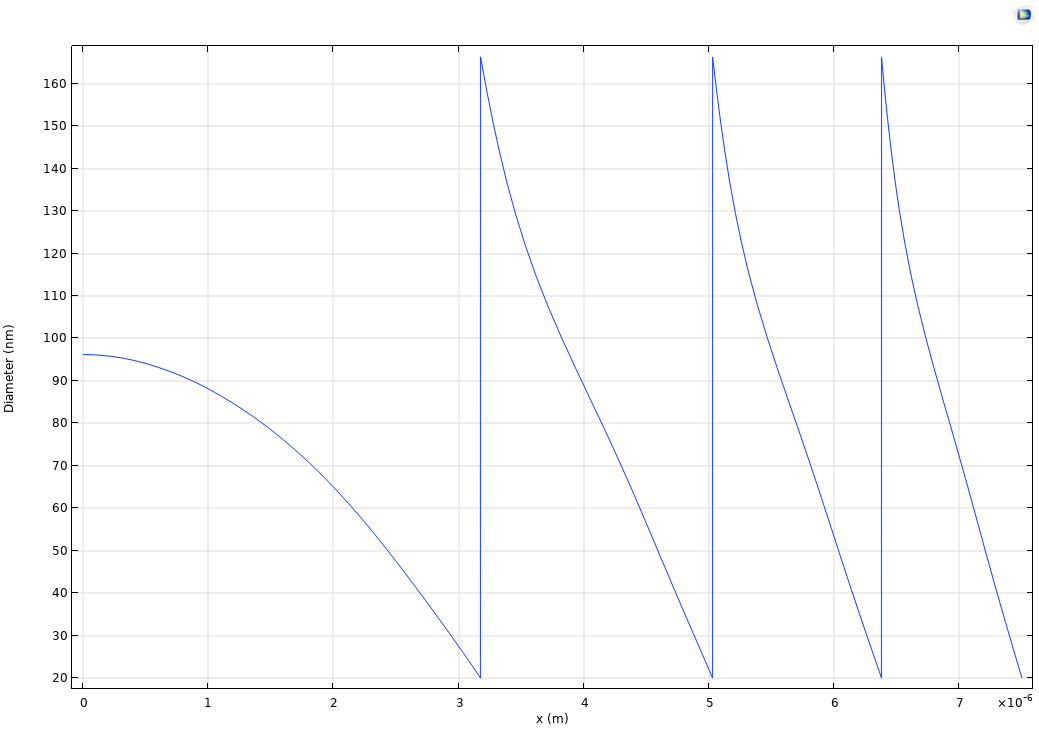
Rozkład średnic nanoprętów D(x) w funkcji odległości od osi optycznej metalowych soczewek o ogniskowej 25~\mu\mathrm{m}, promień 7,5~\mu\mathrm{m}i roboczej długości fali 400~\mathrm{nm}..

Kolejnym wyzwaniem jest przekształcenie tej funkcji w rzeczywistą geometrię. Jeśli zdefiniujemy wyżej wymienione funkcje w formacie Definicje globalne węzeł, możemy zdefiniować nanosłup jako część geometrii z pozycją słupa x jako dane wejściowe i z szerokością ustawioną na D(x). Następnie musimy tylko dodać \lfloor R/P \rfloor (tutaj, R to promień metalenów, a P jest okresem metapowierzchni) instancji tej części do sekwencji geometrii. Co więcej, możemy użyć Application Builder do napisania metody, która zrobi to za nas, jak omówiono w następnej sekcji.

O implementacji aplikacji

Przyjrzyjmy się najpierw, jak zautomatyzować generowanie geometrii metalens. Zasadniczo w kreatorze aplikacji możemy użyć metody model.component(<comp>).geom(<geom>).create(<name>, "PartInstance") aby utworzyć instancję części geometrii, a następnie ustawić parametry wejściowe za pomocą metody model.component(<comp>).geom(<geom>).feature(<name>).setEntry
("inputexpr", <expr-name>, <val>). Umieszczenie tych poleceń wewnątrz pętli for pozwoli nam uzyskać całą metapowierzchnię. Należy zauważyć, że to podejście działa dobrze w przypadku małych meta-powierzchni (R/P\lesssim100) oraz do celów edukacyjnych. W przypadku dużych konstrukcji metalowych konieczne jest zastosowanie hierarchicznego podejścia do submodelowania, w którym COMSOL^® model jest używany do obliczania odpowiedzi komórki elementarnej dla różnych parametrów geometrii i gdzie wynik jest używany jako część większego programu wykorzystującego Javę^® metody lub LiveLink™ dla MATLAB^®. Teraz, gdy mamy już doświadczenie w pisaniu metod, możemy utworzyć przycisk, który pobiera dane wyjściowe początkowej optymalizacji za pomocą model.result().numerical("gev1").getReal() i ustawia parametry modelu na te wartości za pomocą model.param().set(). Dodatkowo użyliśmy setRibbonItemEnabled() aby włączyć przycisk następnego kroku dopiero po zakończeniu poprzednich.

Application Builder pozwala osiągnąć znacznie więcej niż tylko automatyzację bardziej żmudnych kroków w procesie projektowania. Na przykład spakowanie modelu do aplikacji oznacza, że możemy stworzyć niestandardowy interfejs użytkownika (UI), co może być bardzo korzystne, ponieważ użytkownik będzie mógł monitorować cały proces projektowania na pierwszy rzut oka. Poniższy rysunek przedstawia interfejs użytkownika aplikacji. Kolejnym możliwym krokiem jest oczywiście użycie COMSOL Compiler™ do stworzenia samodzielnej aplikacji.

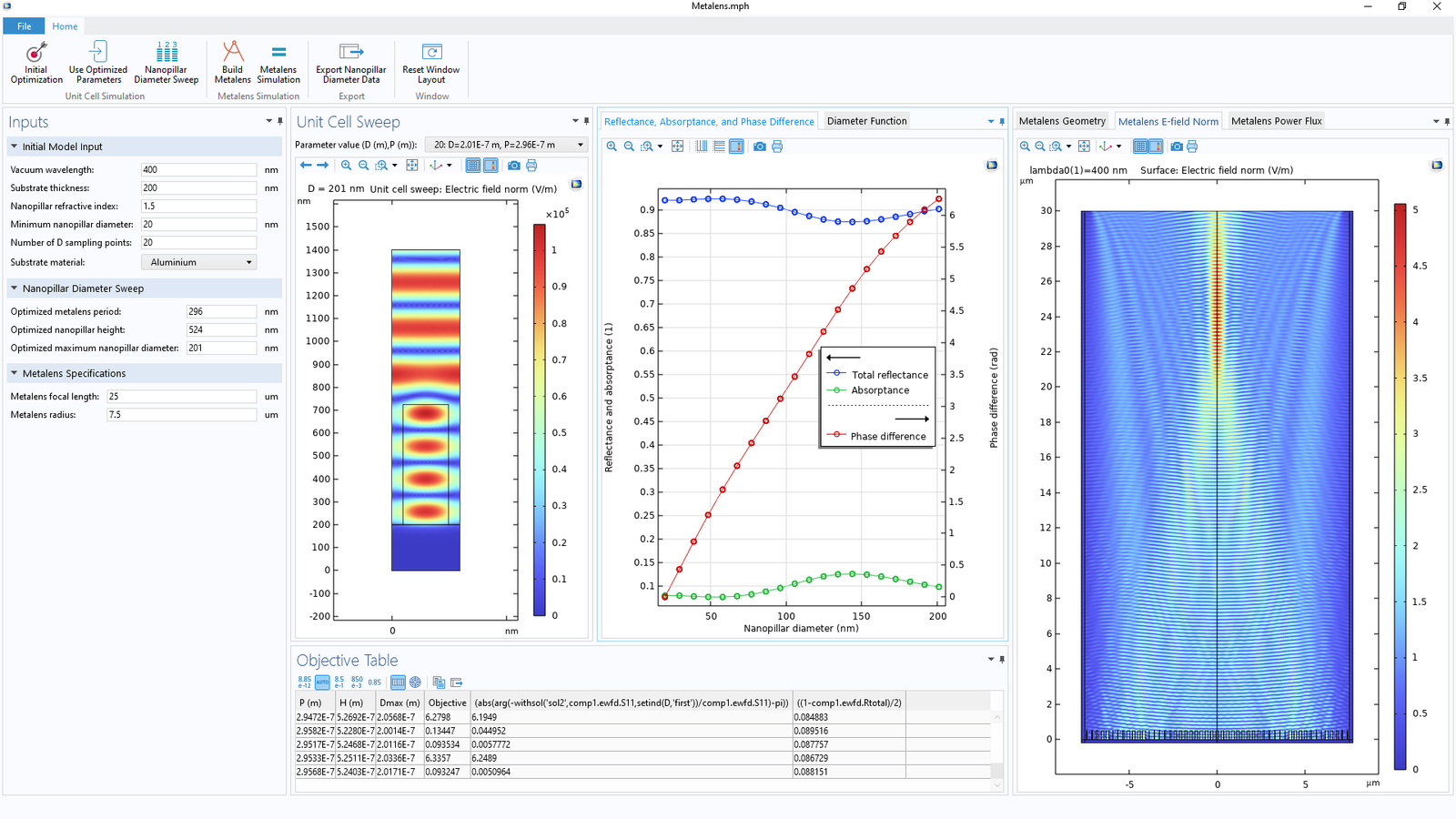
Interfejs użytkownika aplikacji metalens, zaprojektowany tak, aby wszystkie aspekty procesu projektowania mogły być monitorowane na pierwszy rzut oka.

Nagranie ekranu aplikacji metalens w akcji.

Przemyślenia końcowe

W tym wpisie na blogu podsumowaliśmy, jak zbudować aplikację, która może być używana do projektowania dwuwymiarowych metalowych soczewek odblaskowych o określonym rozmiarze, ogniskowej i długości fali roboczej. Zobaczyliśmy, że za pomocą kreatora aplikacji w COMSOL Multiphysics^®Stosunkowo skomplikowany proces projektowania można usprawnić za pomocą interfejsu użytkownika, który umożliwia użytkownikowi wygodne monitorowanie procesu projektowania od początku do końca.

Jednakże, zaledwie zarysowaliśmy powierzchnię projektowania metalens. Dalsze rozszerzenia obejmują uwzględnienie trójwymiarowych soczewek, w tym analizę wydajności soczewek (np. rozmiar ogniskowania i właściwości dyspersyjne, jak przeanalizowano w ref. 1) oraz uwzględnienie multifizyki do modelowania termicznie konfigurowalnych metalenów, jak w ref. 2. 2. Mamy nadzieję zgłębić niektóre z tych bardziej zaawansowanych tematów w przyszłym wpisie na blogu.

Następne kroki

Proszę samodzielnie wypróbować aplikację metalens, klikając poniższy przycisk, który przeniesie Państwa do Galerii aplikacji:

Referencje

1. H. Guo et al., „Design of Polarization-Independent Reflective Metalens in the Ultraviolet-Visible Wavelength Region,” Nanomaterials, vol. 11, no. 5, 2021; https://doi.org/10.3390/nano11051243.
2. A. Archetti et al., „Termicznie rekonfigurowalne metaleny,” Nanophotonics, vol. 11, nr 17, s. 3969-3980, 2022; https://doi.org/10.1515/nanoph-2022-0147.

Oracle i Java są zastrzeżonymi znakami towarowymi firmy Oracle i/lub jej podmiotów stowarzyszonych. MATLAB jest zastrzeżonym znakiem towarowym firmy The MathWorks, Inc.

Join the forum for Designers!

Your expertise is vital to the community. Join us and contribute your knowledge!

Share, learn and grow with the best professionals in the industry.